Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the Hilbert space distance between two discrete quantum states
ResourceFunction["QuantumDistance"][QuantumDiscreteState[qds1,…],QuantumDiscreteState[qds2,…]] returns the fidelity distance (defined below) between the discrete quantum states qds1 and qds2. | |
ResourceFunction["QuantumDistance"][QuantumDiscreteState[qds1,…],QuantumDiscreteState[qds2,…],measure] returns the distance using the Hilbert space distance measure measure. |
| "Fidelity" | 1 minus the fidelity of the two states (i.e. 1 minus the most general probability that the two states will measure to be equivalent) |
| "RelativeEntropy" | relative von Neumann entropy distance between the two states (i.e. the quantum analog of the Kullback–Leibler divergence) |
| "Trace" | trace distance between the density matrices of the two states (i.e. the quantum analog of the Kolmogorov–Smirnov distance) |
| "BuresAngle" | infinitesimal Bures angle distance between the density matrices of the two states (i.e. the quantum analog of the Fisher information metric) |
| "HilbertSchmidt" | Hilbert–Schmidt information distance between the two states |
| "Bloch" | coordinate distance between two qubit states on the Bloch sphere |
Find the default (fidelity) distance between two trivial pure quantum states:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= |
Find the fidelity distance between two mixed quantum states:
| In[4]:= | ![state3 = ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}];
state4 = ResourceFunction["QuantumDiscreteState"][{{1 + I, 0}, {0, 1 - I}}];
ResourceFunction["QuantumDistance"][state3, state4]](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/2218bc88acf0c364.png) |
| Out[4]= |  |
Find the default (fidelity) distance between a pure state and a mixed state:
| In[5]:= | ![state1 = ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}];
state2 = ResourceFunction["QuantumDiscreteState"][{1, -I}];
ResourceFunction["QuantumDistance"][state1, state2]](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/2556176d53119ab9.png) |
| Out[5]= |
Find the trace distance between the same pure state and mixed state:
| In[6]:= |
| Out[6]= |
Find the coordinate distance between two random pure qubit states on the Bloch sphere:
| In[7]:= | ![state1 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
state2 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
ResourceFunction["QuantumDistance"][state1, state2, "Bloch"]](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/3a815efa385b5c0e.png) |
| Out[7]= |
Find the relative von Neumann entropy distance between two random 5-dimensional pure states:
| In[8]:= | ![state1 = ResourceFunction["QuantumDiscreteState"][{"RandomPure", 1}, 5];
state2 = ResourceFunction["QuantumDiscreteState"][{"RandomPure", 1}, 5];
ResourceFunction["QuantumDistance"][state1, state2, "RelativeEntropy"]](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/2fa2b856c369b591.png) |
| Out[8]= |
Find distances between multiqubit states:
| In[9]:= | ![GHZ = ResourceFunction["QuantumDiscreteState"]["GHZ"];
W = ResourceFunction["QuantumDiscreteState"]["W"];
ResourceFunction["QuantumDistance"][GHZ, W, "HilbertSchmidt"]](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/511106186abd511f.png) |
| Out[9]= |
Find distances between higher-dimensional qudit states:
| In[10]:= | ![state1 = ResourceFunction["QuantumDiscreteState"][{1, 1 + I, 1 - I}, 3];
state2 = ResourceFunction["QuantumDiscreteState"][{1/Sqrt[3], I, Sqrt[2/3] - I}, 3];
ResourceFunction["QuantumDistance"][state1, state2, "HilbertSchmidt"]](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/53b7370557e7e44b.png) |
| Out[10]= | 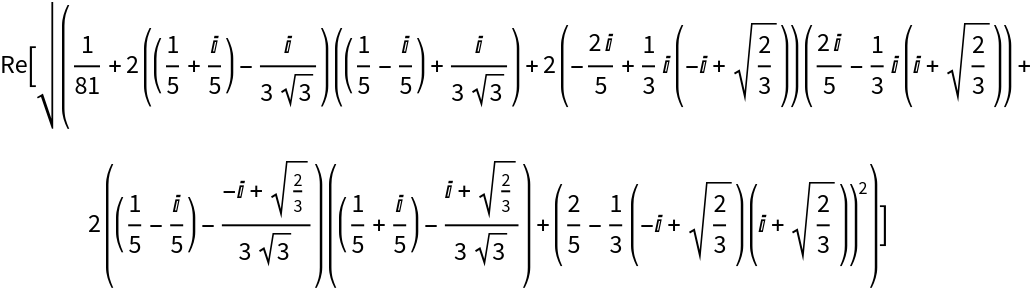 |
Fidelity distances can be computed between any combination of arbitrary pure and mixed states:
| In[11]:= | ![pure1 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
pure2 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
mixed1 = ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}];
mixed2 = ResourceFunction[
"QuantumDiscreteState"][{{1/2 - I, -1/4}, {-1/4, 3/2 + I}}];](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/5b09f33b23c654d6.png) |
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
| In[15]:= |
| Out[15]= |  |
Relative entropy distances can be computed between any combination of arbitrary pure and mixed states:
| In[16]:= | ![pure1 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
pure2 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
mixed1 = ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}];
mixed2 = ResourceFunction[
"QuantumDiscreteState"][{{1/2 - I, -1/4}, {-1/4, 3/2 + I}}];](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/5844d39965c91b9d.png) |
| In[17]:= |
| Out[17]= |
| In[18]:= |
| Out[18]= |
| In[19]:= |
| Out[19]= |
| In[20]:= |
| Out[20]= |
Trace distances can be computed between any combination of arbitrary pure and mixed states:
| In[21]:= | ![pure1 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
pure2 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
mixed1 = ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}];
mixed2 = ResourceFunction[
"QuantumDiscreteState"][{{1/2 - I, -1/4}, {-1/4, 3/2 + I}}];](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/5950d4097781a3c5.png) |
| In[22]:= |
| Out[22]= |
| In[23]:= |
| Out[23]= |
| In[24]:= |
| Out[24]= |
| In[25]:= |
| Out[25]= |
Infinitesimal Bures angle distances can be computed between any combination of arbitrary pure and mixed states:
| In[26]:= | ![pure1 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
pure2 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
mixed1 = ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}];
mixed2 = ResourceFunction[
"QuantumDiscreteState"][{{1/2 - I, -1/4}, {-1/4, 3/2 + I}}];](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/71856a82bff962f5.png) |
| In[27]:= |
| Out[27]= |
| In[28]:= |
| Out[28]= |
| In[29]:= |
| Out[29]= |
| In[30]:= |
| Out[30]= |  |
Hilbert–Schmidt distances can be computed between any combination of arbitrary pure and mixed states:
| In[31]:= | ![pure1 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
pure2 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
mixed1 = ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}];
mixed2 = ResourceFunction[
"QuantumDiscreteState"][{{1/2 - I, -1/4}, {-1/4, 3/2 + I}}];](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/0ecf5a2dd2b84071.png) |
| In[32]:= |
| Out[32]= |
| In[33]:= |
| Out[33]= |
| In[34]:= |
| Out[34]= |
| In[35]:= |
| Out[35]= |
Coordinate distances on the Bloch sphere can be computed between any combination of arbitrary pure and mixed qubit (2-dimensional) states:
| In[36]:= | ![pure1 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
pure2 = ResourceFunction["QuantumDiscreteState"]["RandomPure"];
mixed1 = ResourceFunction[
"QuantumDiscreteState"][{{1/4 + I, 1/2}, {1/2, 3/4 - I}}];
mixed2 = ResourceFunction[
"QuantumDiscreteState"][{{1/2 - I, -1/4}, {-1/4, 3/2 + I}}];](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/1296cc5e9d6c4702.png) |
| In[37]:= |
| Out[37]= |
| In[38]:= |
| Out[38]= |
| In[39]:= |
| Out[39]= |
| In[40]:= |
| Out[40]= |
However, Bloch distances cannot be computed for arbitrary qudit (higher-dimensional) states (returns unevaluated):
| In[41]:= | ![pure3 = ResourceFunction["QuantumDiscreteState"][{"RandomPure", 1}, 3];
pure4 = ResourceFunction["QuantumDiscreteState"][{"RandomPure", 1}, 3];
ResourceFunction["QuantumDistance"][pure3, pure4, "Bloch"]](https://www.wolframcloud.com/obj/resourcesystem/images/f2f/f2f3d36a-d085-4f6b-978f-7590a4fe3dc1/270bd4e353b59cf5.png) |
| Out[41]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License