Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 QuantumDiscreteOperatorToZXDiagram

Source Notebook

Convert a discrete quantum operator into a ZX-diagram

Contributed by: Jonathan Gorard (with modifications by Manojna Namuduri)

ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][QuantumDiscreteOperator[…]]

converts the specified QuantumDiscreteOperator into an equivalent ZXDiagramObject.

Details

If ResourceFunction["QuantumDiscreteOperatorToZXDiagram"] succeeds in converting the specified QuantumDiscreteOperator into a ZX-diagram, it will return a ZXDiagramObject expression.
ResourceFunction["QuantumDiscreteOperatorToZXDiagram"] works by partially tracing out subsystems in the specified QuantumDiscreteOperator, and then attempting to decompose those subsystems into sequential compositions of Z-spider and X-spider generators (i.e. sequential compositions of rotations around the z axis and the x axis of the Bloch sphere, respectively), before taking the tensor product of the resulting subdiagrams to yield the desired ZXDiagramObject. Any subsystems that are not found to be equivalent to a recognizable sequential composition of Z-spider and X-spider generators are omitted.
Whenever the specified QuantumDiscreteOperator cannot be converted into an equivalent ZXDiagramObject via the above procedure, ResourceFunction["QuantumDiscreteOperatorToZXDiagram"] will return Indeterminate.
The generators/spiders produced within the resulting ZXDiagramObject can have arbitrary input and output arities.
In the resulting ZXDiagramObject, the following properties are supported:
"LabeledGraph"graph form of the ZX-diagram with phases labeled
"UnlabeledGraph"graph form of the ZX-diagram without phases labeled
"OperatorForm"ZX-diagram represented as a tensor product of generators
"ListForm"ZX-diagram represented as a list of generators
"MatrixForm"ZX-diagram represented as an explicit linear map on qubits
"ZSpiders"list of Z-spiders in the ZX-diagram
"XSpiders"list of X-spiders in the ZX-diagram
"HadamardGates"list of Hadamard gates in the ZX-diagram
"Diamonds"list of black diamonds in the ZX-diagram
"Wires"list of wires in the ZX-diagram
"ZSpiderCount"number of Z-spiders in the ZX-diagram
"XSpiderCount"number of X-spiders in the ZX-diagram
"HadamardGateCount"number of Hadamard gates in the ZX-diagram
"DiamondCount"number of black diamonds in the ZX-diagram
"WireCount"number of wires in the ZX-diagram
ResourceFunction["QuantumDiscreteOperatorToZXDiagram"] names the ZX generators in the resulting ZXDiagramObject in the conventional way, naming Z-spiders as z1,z2,…; X-spiders as x1,x2,…; black diamonds as d1,d2,…; inputs as i1,i2,…; outputs as o1,o2,…; etc.

Examples

Basic Examples (7) 

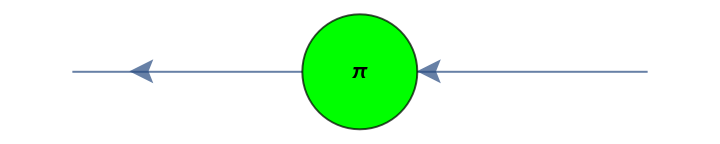
Convert an arity-1 discrete quantum operator (a Pauli-Z gate) into a single-spider ZX-diagram:

In[1]:=
diagram = ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][ ResourceFunction["QuantumDiscreteOperator"]["PauliZ"]]
Out[1]=
In[2]:=
diagram["OperatorForm"]
Out[2]=
In[3]:=
diagram["LabeledGraph"]
Out[3]=

Convert a different arity-1 discrete quantum operator (a Hadamard gate) into a three-spider ZX-diagram:

In[4]:=
operator2 = ResourceFunction["QuantumDiscreteOperator"]["Hadamard"]
Out[4]=
In[5]:=
diagram2 = ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator2]
Out[5]=
In[6]:=
diagram2["OperatorForm"]
Out[6]=
In[7]:=
diagram2["LabeledGraph"]
Out[7]=

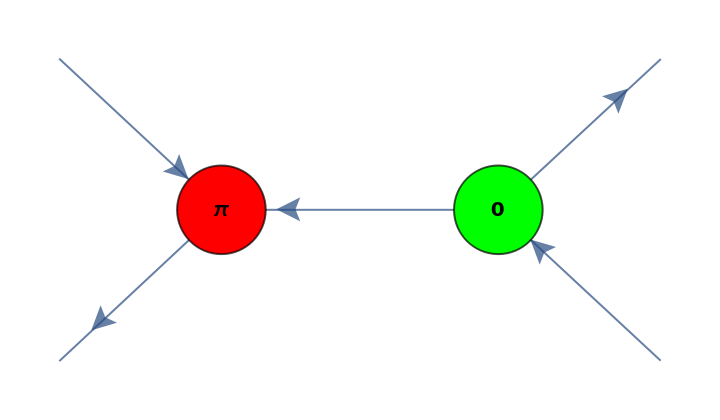
Convert an arity-2 discrete quantum operator (a CNOT gate) into a two-spider ZX-diagram:

In[8]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["CNOT", {1, 2}]
Out[8]=
In[9]:=
diagram = ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator]
Out[9]=
In[10]:=
diagram["OperatorForm"]
Out[10]=
In[11]:=
diagram["LabeledGraph"]
Out[11]=

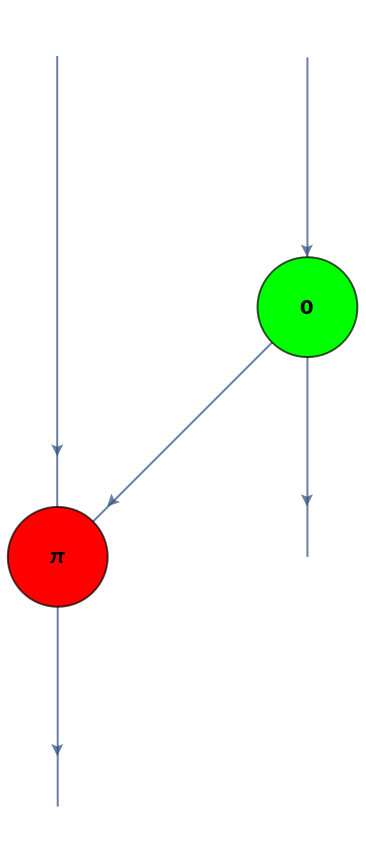
Show the layered graph form of the ZX-diagram with the inputs at the top:

In[12]:=
LayeredGraphPlot[diagram["LabeledGraph"], {i1, i2} -> Automatic]
Out[12]=

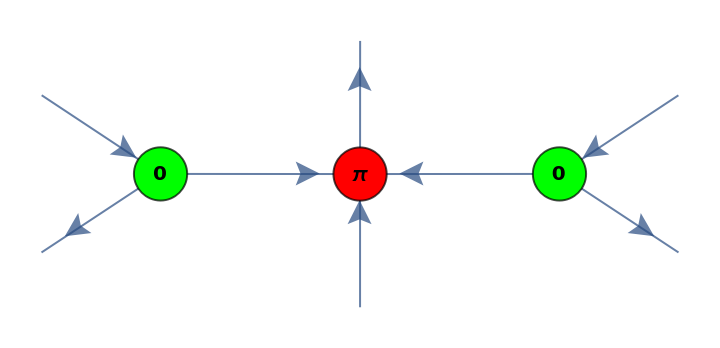
Convert a CNOT gate with an additional control qubit (i.e. an arity-3 Toffoli gate) into a three-spider ZX-diagram:

In[13]:=
operator2 = ResourceFunction["QuantumDiscreteOperator"]["Toffoli", {1, 2, 3}]
Out[13]=
In[14]:=
diagram2 = ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator2]
Out[14]=
In[15]:=
diagram2["OperatorForm"]
Out[15]=
In[16]:=
diagram2["LabeledGraph"]
Out[16]=

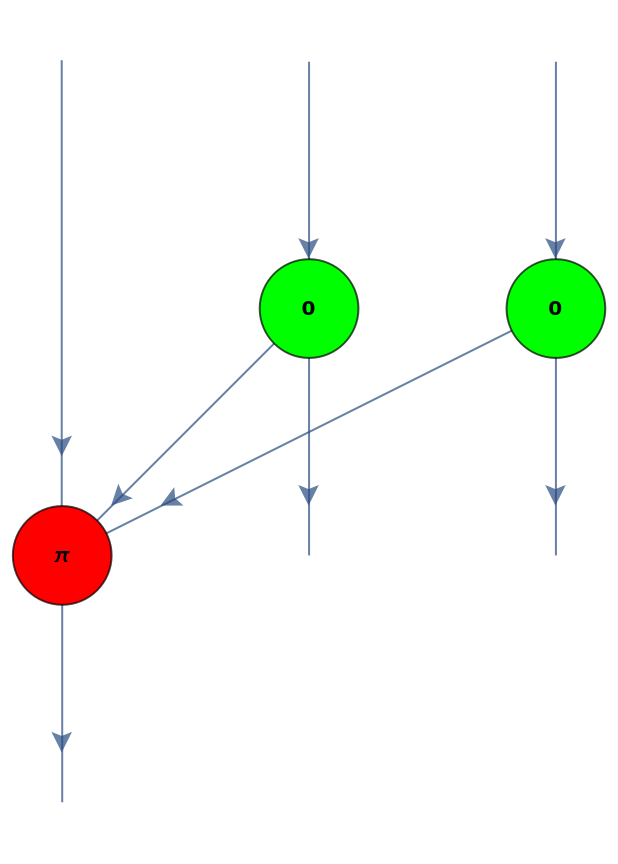
Show the layered graph form of the ZX-diagram with the inputs at the top:

In[17]:=
LayeredGraphPlot[diagram2["LabeledGraph"], {i1, i2, i3} -> Automatic]
Out[17]=

Convert a more complicated arity-3 quantum Fourier transform operator into a 15-spider ZX-diagram:

In[18]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["Fourier", {1, 2, 3}]
Out[18]=
In[19]:=
diagram = ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator]
Out[19]=
In[20]:=
diagram["OperatorForm"]
Out[20]=
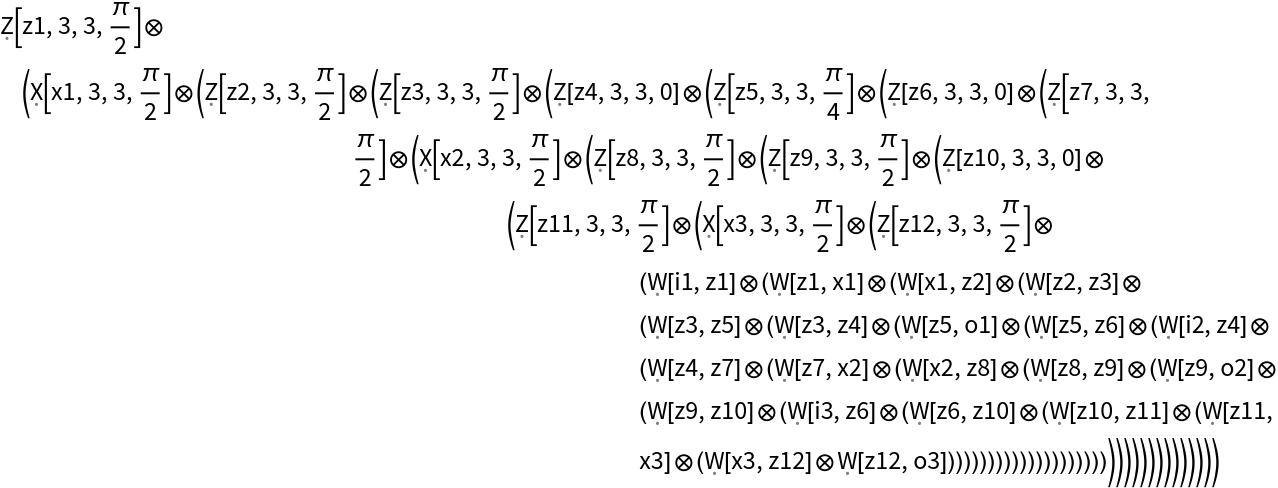
In[21]:=
diagram["LabeledGraph"]
Out[21]=

Show the layered graph form of the ZX-diagram with the inputs at the top:

In[22]:=
LayeredGraphPlot[diagram["LabeledGraph"], {i1, i2, i3} -> Automatic]
Out[22]=

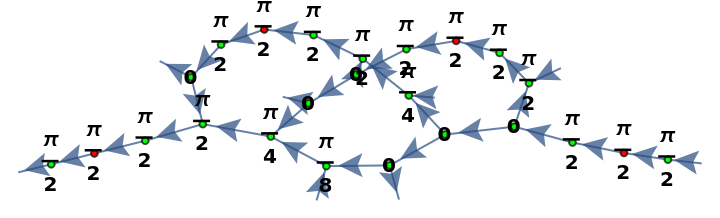
Convert an arity-4 inverse quantum Fourier transform operator into a 24-spider ZX-diagram:

In[23]:=
operator2 = ResourceFunction["QuantumDiscreteOperator"][ "InverseFourier", {1, 2, 3, 4}]
Out[23]=
In[24]:=
diagram2 = ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator2]
Out[24]=
In[25]:=
diagram2["LabeledGraph"]
Out[25]=

Show the layered graph form of the ZX-diagram with the inputs at the top:

In[26]:=
LayeredGraphPlot[ diagram2["LabeledGraph"], {i1, i2, i3, i4} -> Automatic]
Out[26]=

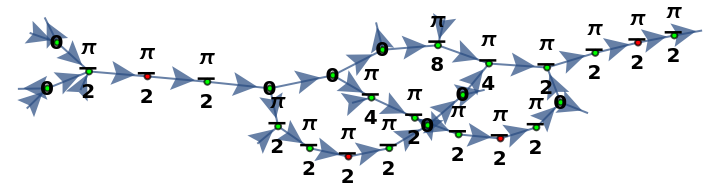
Convert an inverse quantum Fourier transform operator with two additional control qubits into a 26-spider ZX-diagram:

In[27]:=
operator3 = ResourceFunction["QuantumDiscreteOperator"][{"ControlledU", ResourceFunction["QuantumDiscreteOperator"][ "InverseFourier", {1, 2, 3, 4}]}, {1, 2, 3, 4, 5, 6}]
Out[27]=
In[28]:=
diagram3 = ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator3]
Out[28]=
In[29]:=
diagram3["LabeledGraph"]
Out[29]=

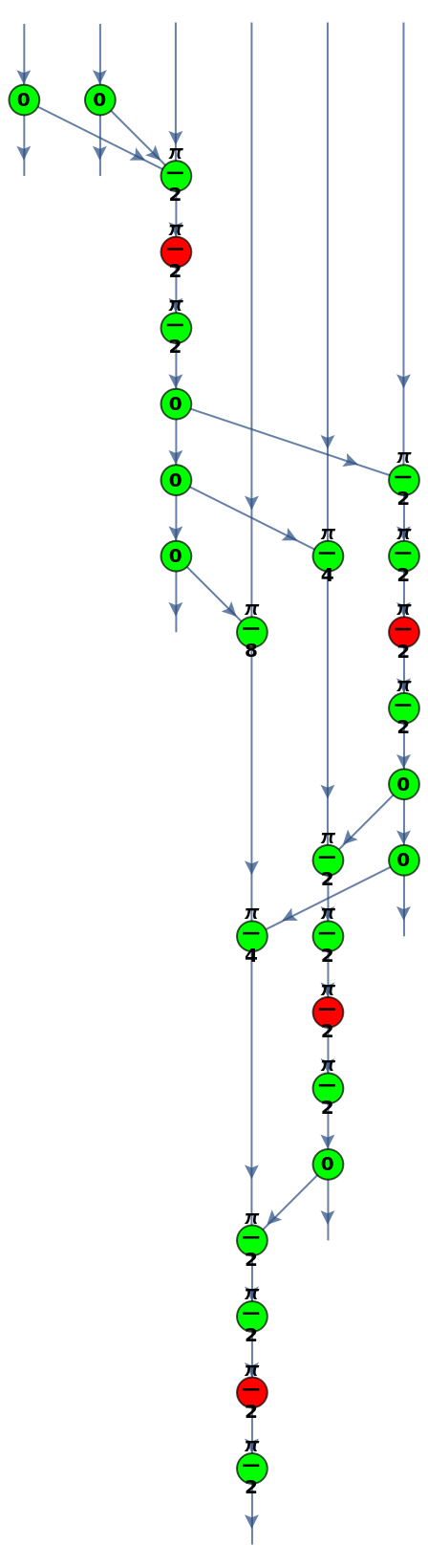
Show the layered graph form of the ZX-diagram with the inputs at the top:

In[30]:=
LayeredGraphPlot[ diagram3["LabeledGraph"], {i1, i2, i3, i4, i5, i6} -> Automatic]
Out[30]=

Scope (13) 

If the specified QuantumDiscreteOperator object cannot be expressed as a ZX-diagram, QuantumDiscreteOperatorToZXDiagram will return Indeterminate:

In[31]:=
operator = ResourceFunction["QuantumDiscreteOperator"][ "RandomUnitary", {1, 2, 3}]
Out[31]=
In[32]:=
ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator]
Out[32]=

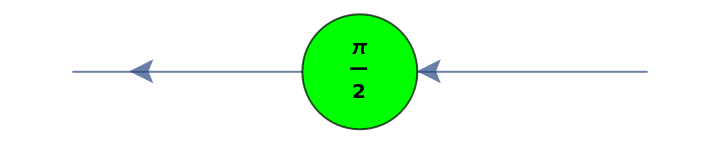
Convert an S-gate (a π/2 phase change gate) to a ZX-diagram:

In[33]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["S"]; ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][ operator]["LabeledGraph"]
Out[33]=

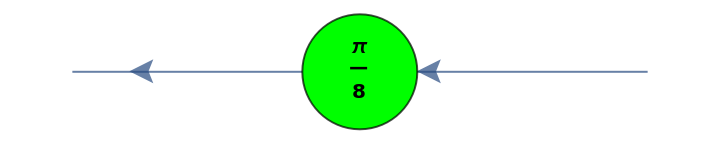
Convert a T-gate (a π/8 phase change gate) to a ZX-diagram:

In[34]:=
operator2 = ResourceFunction["QuantumDiscreteOperator"]["T"]; ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][ operator2]["LabeledGraph"]
Out[34]=

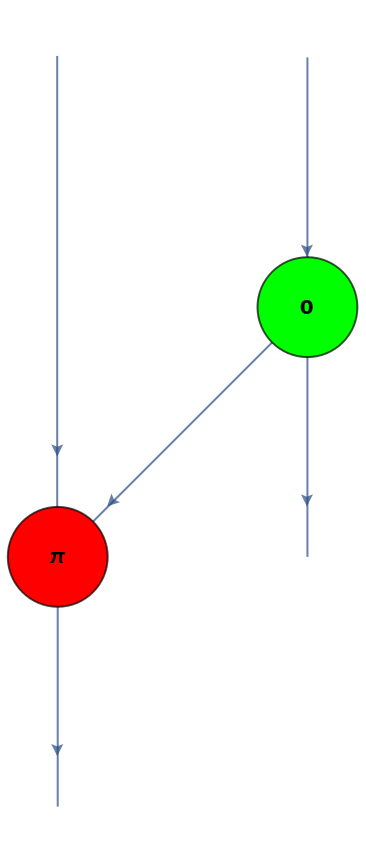
Convert a CNOT gate (a controlled NOT gate) to a ZX-diagram:

In[35]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["CNOT"]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator][ "LabeledGraph"], {i1, i2} -> Automatic]
Out[35]=

Convert a CPHASE gate (a controlled π phase change gate) to a ZX-diagram:

In[36]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["CPHASE"]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator][ "LabeledGraph"], {i1, i2} -> Automatic]
Out[36]=

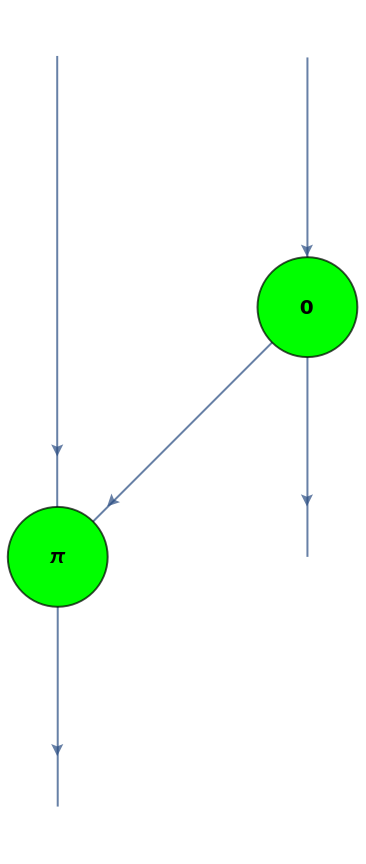
Convert a CX gate (a controlled Pauli-X gate—equivalent to a CNOT) to a ZX-diagram:

In[37]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["CX"]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator][ "LabeledGraph"], {i1, i2} -> Automatic]
Out[37]=

Convert a CY gate (a controlled Pauli-Y gate) to a ZX-diagram:

In[38]:=
operator2 = ResourceFunction["QuantumDiscreteOperator"]["CY"]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator2][ "LabeledGraph"], {i1, i2} -> Automatic]
Out[38]=

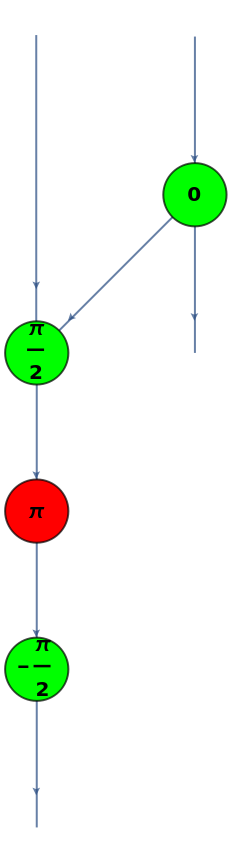
Convert a CZ gate (a controlled Pauli-Z gate) to a ZX-diagram:

In[39]:=
operator3 = ResourceFunction["QuantumDiscreteOperator"]["CZ"]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator3][ "LabeledGraph"], {i1, i2} -> Automatic]
Out[39]=

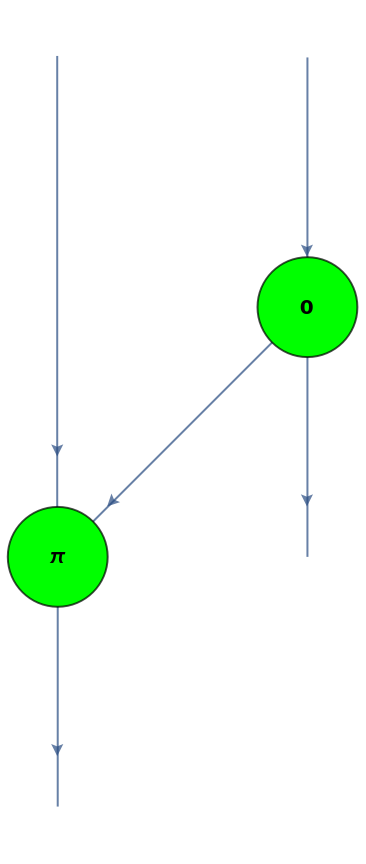
Convert a controlled-U gate (with U being a 2-by-2 Hadamard matrix) to a ZX-diagram with one control qubit:

In[40]:=
operator = ResourceFunction["QuantumDiscreteOperator"][{"ControlledU", HadamardMatrix[2]}, {1, 2}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator][ "LabeledGraph"], {i1, i2} -> Automatic]
Out[40]=

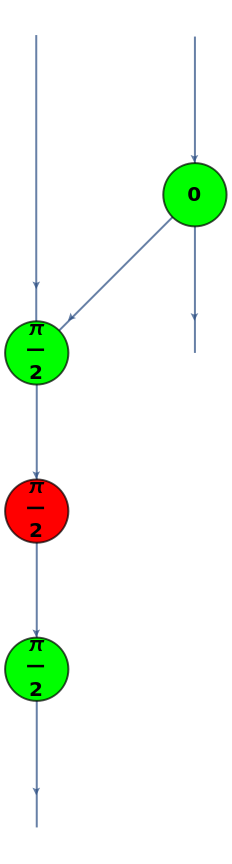
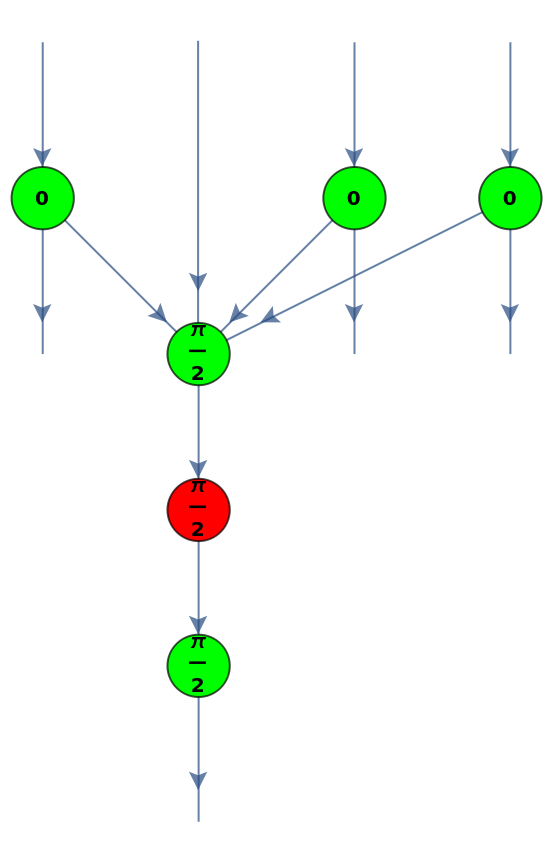
Convert a controlled-U gate (with U being a 2-by-2 Hadamard matrix) to a ZX-diagram with three control qubits instead:

In[41]:=
operator2 = ResourceFunction["QuantumDiscreteOperator"][{"ControlledU", HadamardMatrix[2]}, {1, 2, 3, 4}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator2][ "LabeledGraph"], {i1, i2, i3, i4} -> Automatic]
Out[41]=

Convert a single-qubit QFT gate (quantum Fourier transform) to a ZX-diagram:

In[42]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["Fourier", {1}]; ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][ operator]["LabeledGraph"]
Out[42]=

Convert a two-qubit QFT gate (quantum Fourier transform) to a ZX-diagram:

In[43]:=
operator2 = ResourceFunction["QuantumDiscreteOperator"]["Fourier", {1, 2}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator2][ "LabeledGraph"], {i1, i2} -> Automatic]
Out[43]=

Convert a three-qubit QFT gate (quantum Fourier transform) to a ZX-diagram:

In[44]:=
operator3 = ResourceFunction["QuantumDiscreteOperator"]["Fourier", {1, 2, 3}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator3][ "LabeledGraph"], {i1, i2, i3} -> Automatic]
Out[44]=

Convert a four-qubit QFT gate (quantum Fourier transform) to a ZX-diagram:

In[45]:=
operator4 = ResourceFunction["QuantumDiscreteOperator"]["Fourier", {1, 2, 3, 4}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator4][ "LabeledGraph"], {i1, i2, i3, i4} -> Automatic]
Out[45]=

Convert a single-qubit IQFT gate (inverse quantum Fourier transform) to a ZX-diagram:

In[46]:=
operator5 = ResourceFunction["QuantumDiscreteOperator"]["InverseFourier", {1}]; ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][ operator5]["LabeledGraph"]
Out[46]=

Convert a two-qubit IQFT gate (inverse quantum Fourier transform) to a ZX-diagram:

In[47]:=
operator6 = ResourceFunction["QuantumDiscreteOperator"][ "InverseFourier", {1, 2}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator6][ "LabeledGraph"], {i1, i2} -> Automatic]
Out[47]=

Convert a three-qubit IQFT gate (inverse quantum Fourier transform) to a ZX-diagram:

In[48]:=
operator7 = ResourceFunction["QuantumDiscreteOperator"][ "InverseFourier", {1, 2, 3}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator7][ "LabeledGraph"], {i1, i2, i3} -> Automatic]
Out[48]=

Convert a four-qubit IQFT gate (inverse quantum Fourier transform) to a ZX-diagram:

In[49]:=
operator8 = ResourceFunction["QuantumDiscreteOperator"][ "InverseFourier", {1, 2, 3, 4}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator8][ "LabeledGraph"], {i1, i2, i3, i4} -> Automatic]
Out[49]=

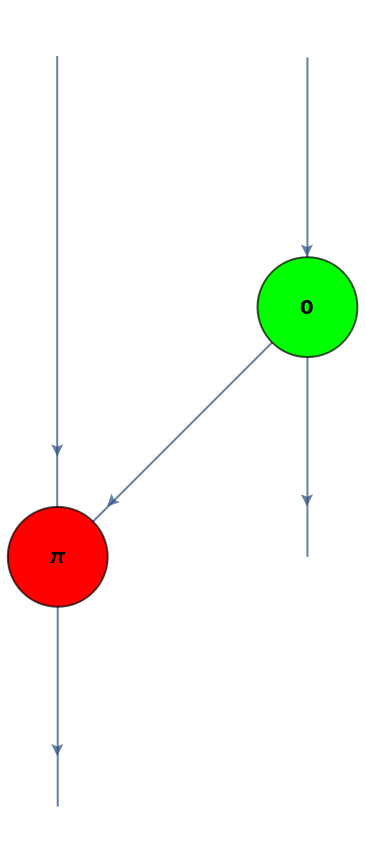
Convert a SUM gate (a half-adder for qubits—similar to a CNOT gate) to a ZX-diagram:

In[50]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["SUM", {1, 2}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator][ "LabeledGraph"], {i1, i2} -> Automatic]
Out[50]=

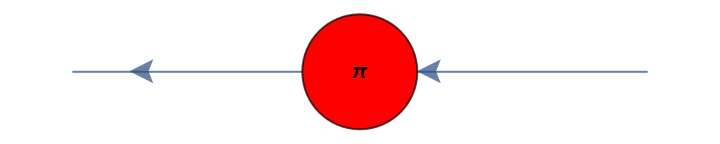
Convert a Pauli-X gate (a π rotation around the x axis of the Bloch sphere) to a ZX-diagram:

In[51]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["PauliX"]; ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][ operator]["LabeledGraph"]
Out[51]=

Convert a Pauli-Y gate (a π rotation around the y axis of the Bloch sphere) to a ZX-diagram:

In[52]:=
operator2 = ResourceFunction["QuantumDiscreteOperator"]["PauliY"]; ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][ operator2]["LabeledGraph"]
Out[52]=

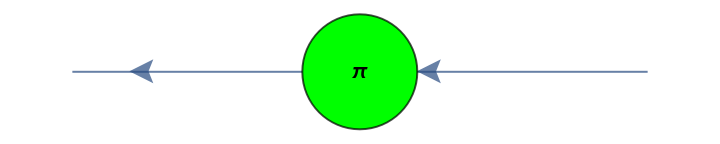
Convert a Pauli-Z gate (a π rotation around the z axis of the Bloch sphere) to a ZX-diagram:

In[53]:=
operator3 = ResourceFunction["QuantumDiscreteOperator"]["PauliZ"]; ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][ operator3]["LabeledGraph"]
Out[53]=

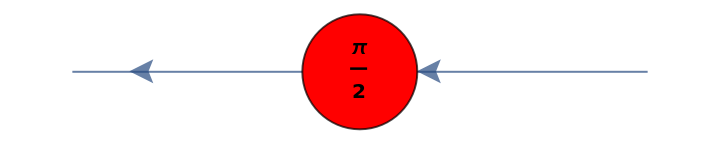
Convert the square root of a NOT gate (half a Pauli-X rotation) to a ZX-diagram:

In[54]:=
operator4 = ResourceFunction["QuantumDiscreteOperator"]["RootNOT"]; ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][ operator4]["LabeledGraph"]
Out[54]=

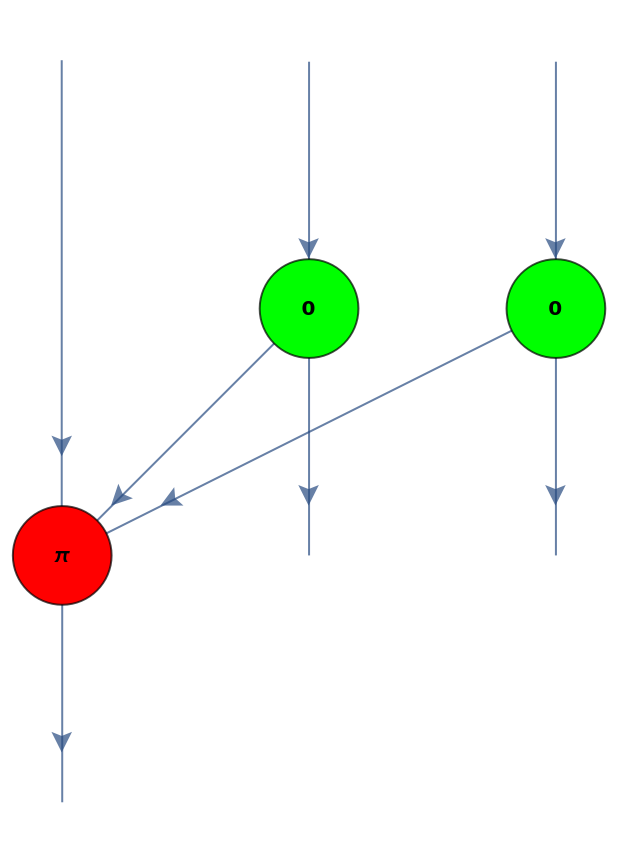
Convert a Toffoli gate (a π/2 Deutsch gate) to a ZX-diagram:

In[55]:=
operator = ResourceFunction["QuantumDiscreteOperator"]["Toffoli", {1, 2, 3}]; LayeredGraphPlot[ ResourceFunction["QuantumDiscreteOperatorToZXDiagram"][operator][ "LabeledGraph"], {i1, i2, i3} -> Automatic]
Out[55]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 08 June 2021

Source Metadata

  • Citation:
    • Bob Coecke and Ross Duncan (2011), "Interacting Quantum Observables: Categorical Algebra and Diagrammatics"
    • Jonathan Gorard, Manojna Namuduri and Xerxes Arsiwalla (2020), "ZX-Calculus and Extended Hypergraph Rewriting Systems I: A Multiway Approach to Categorical Quantum Information Theory"
    • Jonathan Gorard, Manojna Namuduri and Xerxes Arsiwalla (2021), "ZX-Calculus and Extended Wolfram Model Systems II: Fast Diagrammatic Reasoning with an Application to Quantum Circuit Simplification"

Related Resources

Author Notes

QuantumDiscreteOperatorToZXDiagram currently uses global symbols like z1 and x1. Local definition or values for those symbols can cause QuantumDiscreteOperatorToZXDiagram to have unexpected results.

License Information