Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Recover a Jacobi matrix from a list of abscissa-weight pairs
ResourceFunction["QuadratureWeightsToJacobiMatrix"][{{x1,w1},{x2,w2},…}] returns a list {j,c}, where j is the Jacobi matrix corresponding to the quadrature rule represented by the abscissa-weight pairs {xi,wi} and normalization factor c. |
The resource function GaussianQuadratureWeights gives a list of abscissa-weight pairs for Gauss-Legendre quadrature:
| In[1]:= |
| Out[1]= |  |
Recover the corresponding Jacobi matrix and normalization factor:
| In[2]:= |
| Out[2]= |
Use the resource function GeneralizedGaussianQuadratureWeights to generate a Gauss-Laguerre quadrature rule:
| In[3]:= |
| Out[3]= |  |
Recover the Jacobi matrix and normalization factor from the quadrature data:
| In[4]:= |
| Out[4]= |
Compare the recovered Jacobi matrix with the result of the resource function JacobiMatrix:
| In[5]:= |
| Out[5]= |
The normalization factor is equal to the sum of the weights:
| In[6]:= |
| Out[6]= |
QuadratureWeightsToJacobiMatrix can be used even on non-Gaussian quadrature rules. Build a Jacobi matrix from a Newton-Cotes rule:
| In[7]:= |
| Out[7]= |
The resulting Jacobi matrix is unsymmetric because some the weights of the quadrature rule are negative:
| In[8]:= |
| Out[8]= | 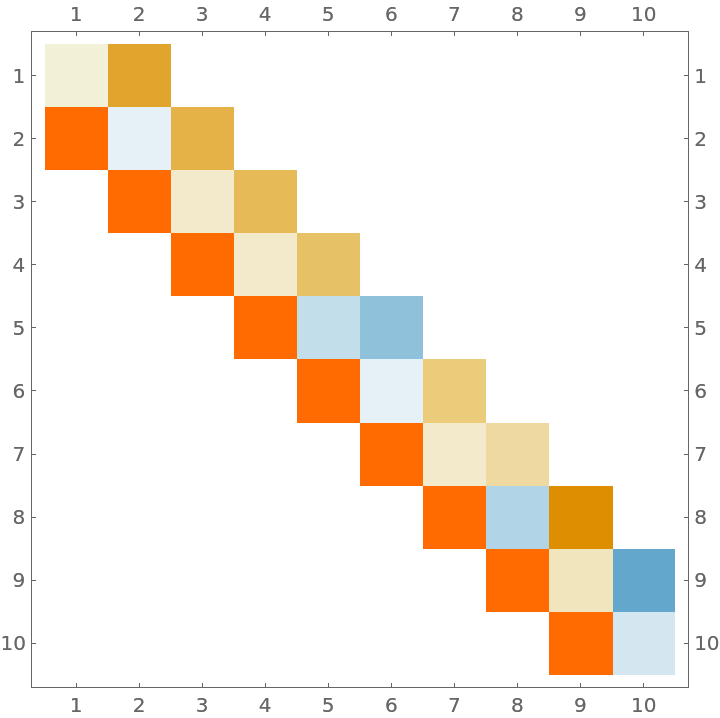 |
A Clenshaw-Curtis rule whose weights are all positive will yield a symmetric Jacobi matrix:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= | 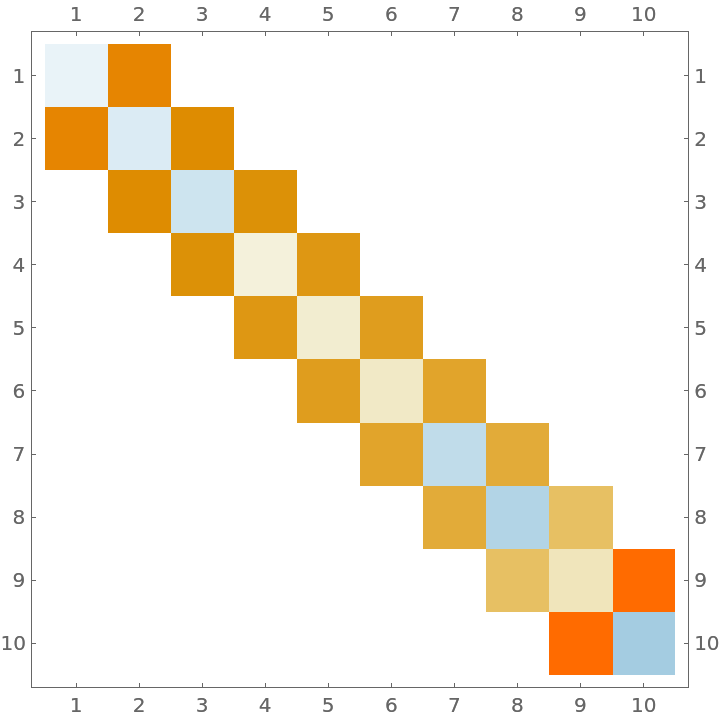 |
This work is licensed under a Creative Commons Attribution 4.0 International License