Basic Examples (8)
A system that starts at -1:
The state and input weights:
The initial value of the gain:
The total simulations is 30 with a batch consisting of 10 simulations:
Compute the controller:
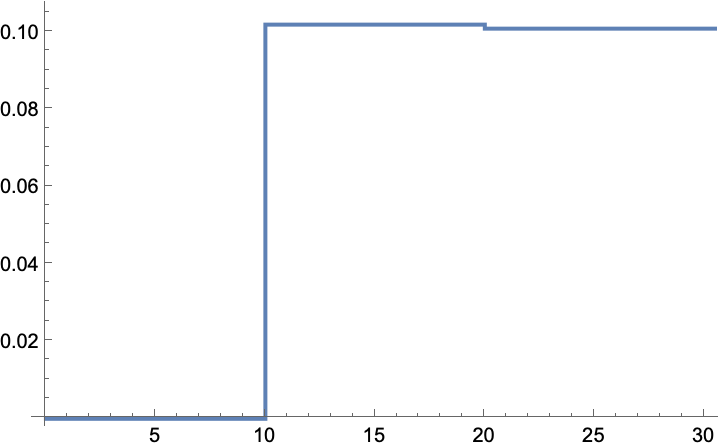
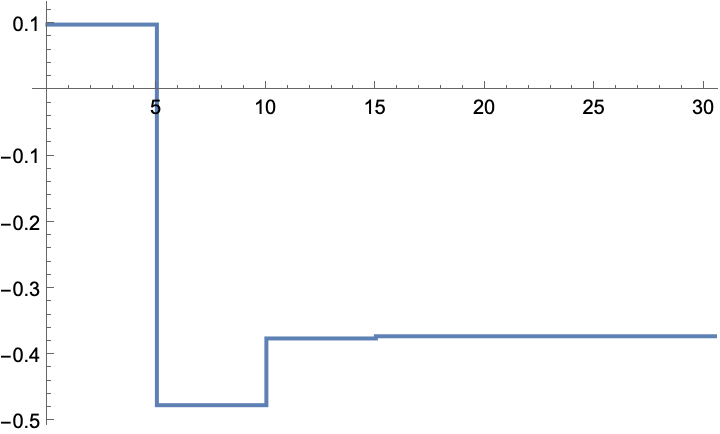
The gain converges to ~0.1:
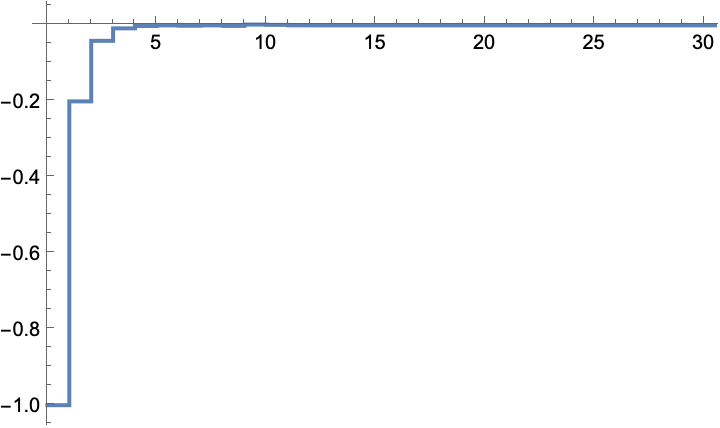
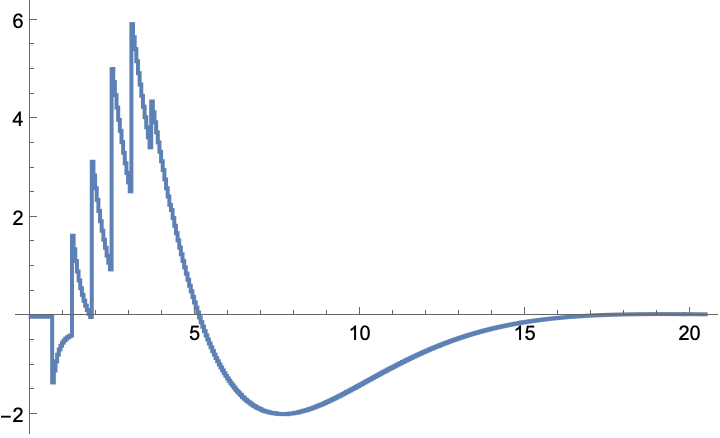
The state is regulated to the origin:
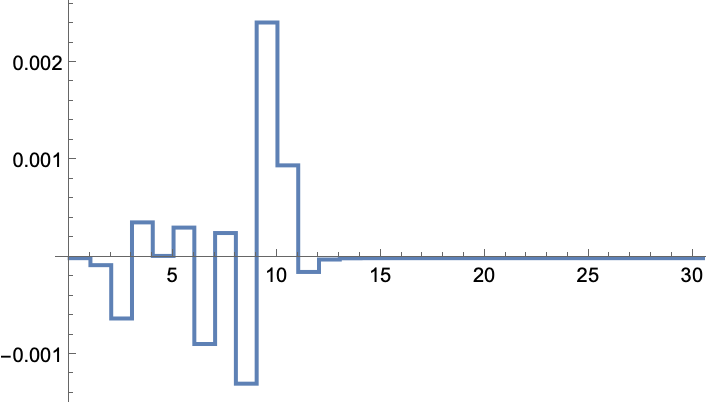
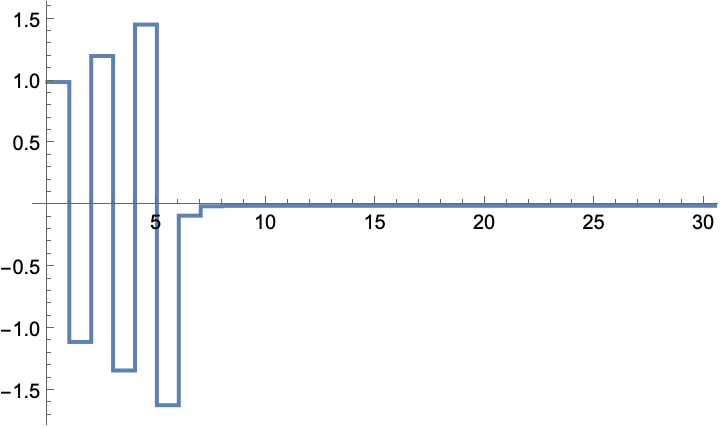
The input sequence that was used during the simulation:
Scope (6)
A system with one state and one input:
Compute a controller:
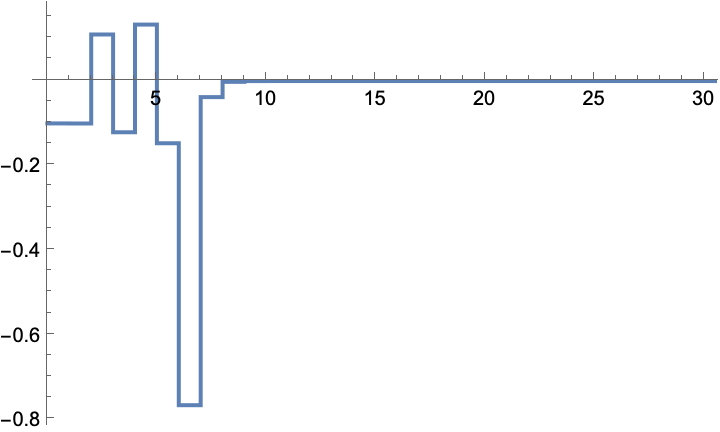
The gain values:
The state is regulated to the origin:
The input sequence that was used during the simulation:
A multi-state system:
Compute a controller:
The gain values:
The states are regulated to the origin:
The input sequence that was used during the simulation:
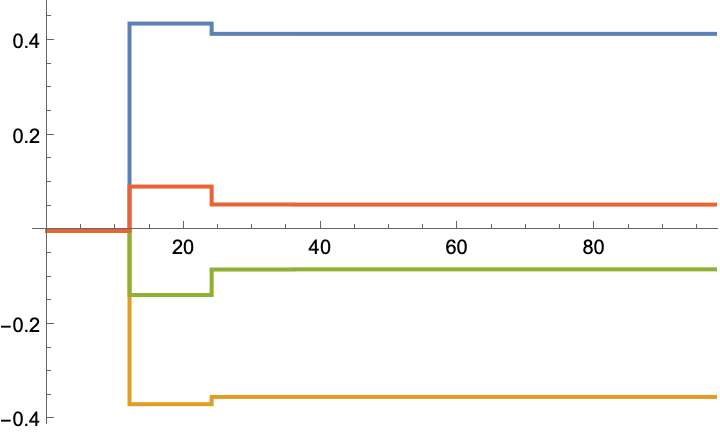
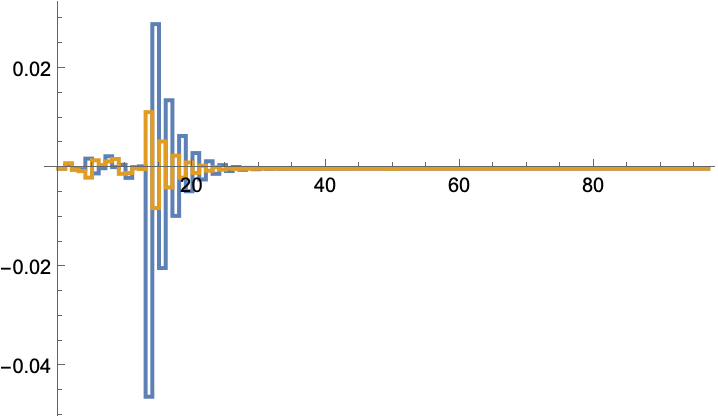
A multi-state, multi-input system:
Compute a controller:
The gain values:
The states are regulated to the origin:
The input sequence that was used during the simulation:
A state-space model:
Compute a controller:
The gain values:
The states are regulated to the origin:
The input sequence that was used during the simulation:
By default, a SystemsModelControllerData object is returned:
It can be used to obtain various properties:
The value of a specific property:
A list of property values:
The values of all properties as an Association:
As a Dataset:
Get a property directly:
Applications (7)
The model of the U.S Coast Guard cutter Tampa based on sea-trials data that gives the heading in response to rudder angle inputs:
Discretize the model:
The model is marginally stable:
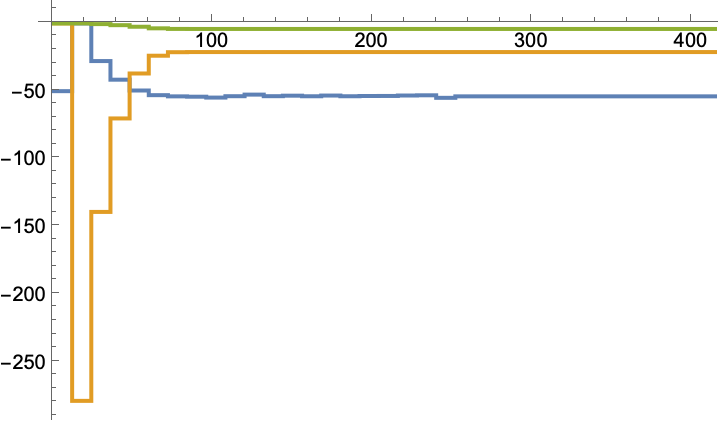
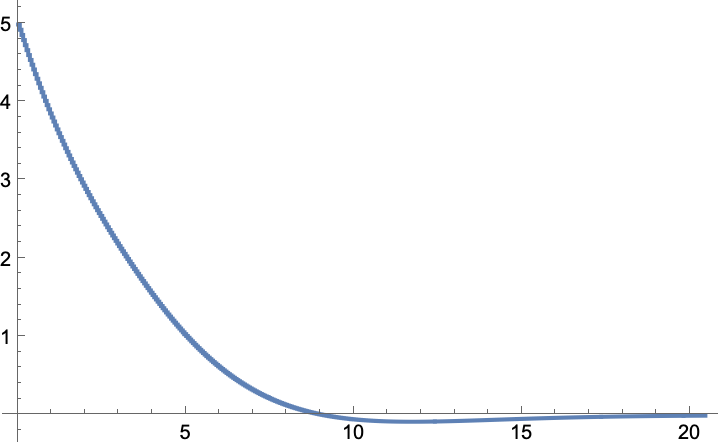
A Q-learning LQ regulator starting with an initial heading of 5°:
The computed gain values:
The heading is regulated back to the origin in about 20 seconds:
The rudder input values:
Properties and Relations (2)
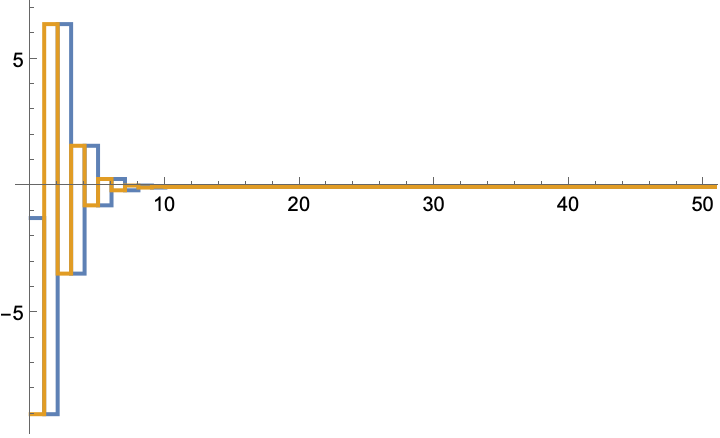
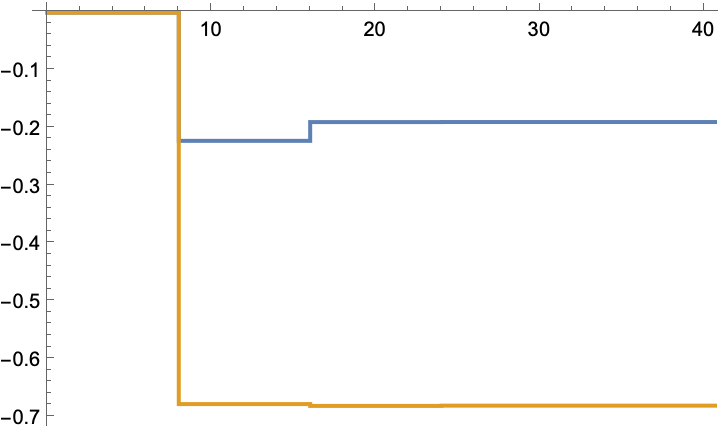
The gain computed by simulation converges to the optimal solution:
The optimal solution computed with knowledge of the system's dynamics:
The above solution is computed using the discrete algebraic Riccati equation:
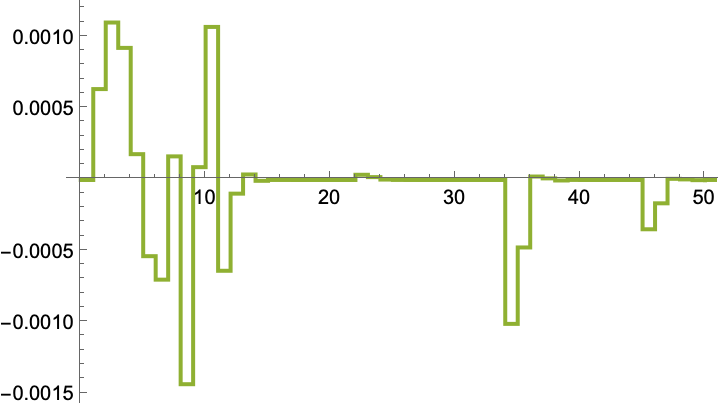
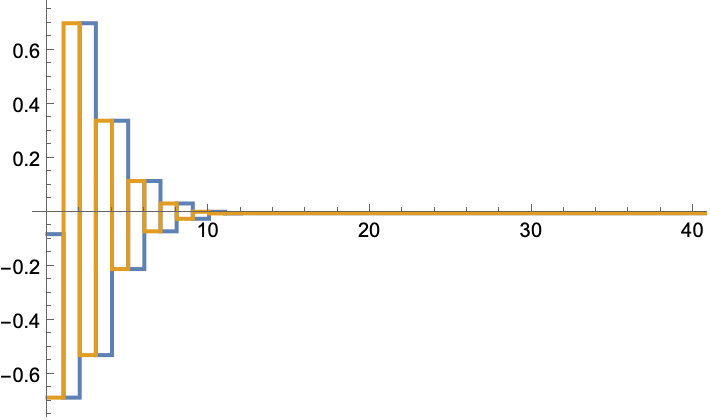
The gain computed by simulation converges to the optimal solution for a nonlinear system:
The optimal solution computed using the linearized model:
The above solution is computed using the discrete algebraic Riccati equation:
Possible Issues (4)
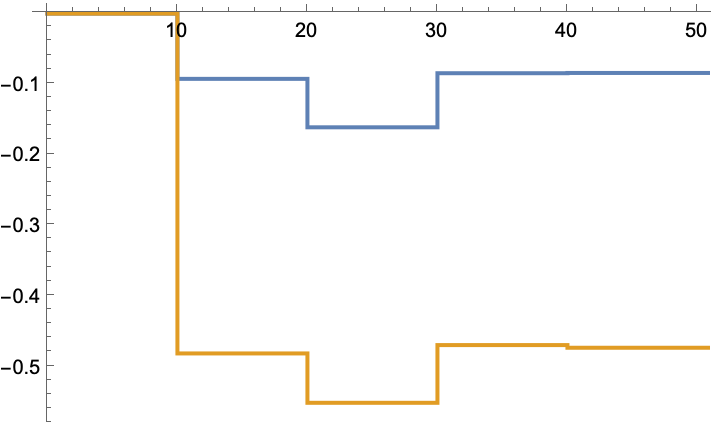
An unstable system may not converge to the optimal solution:
Adjusting the initial gain causes it to converge to the optimal solution:
The optimal solution:
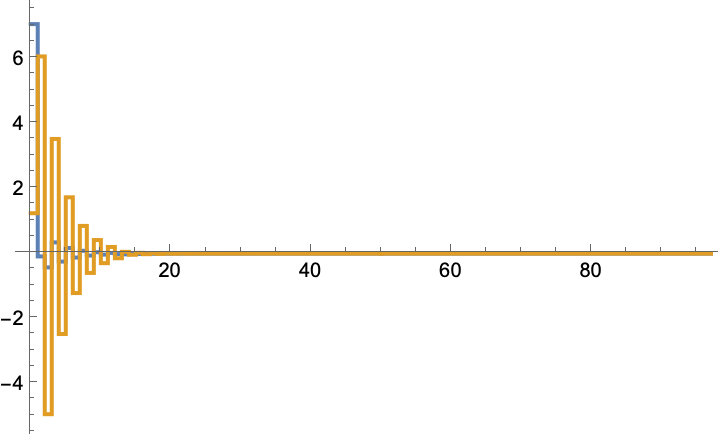
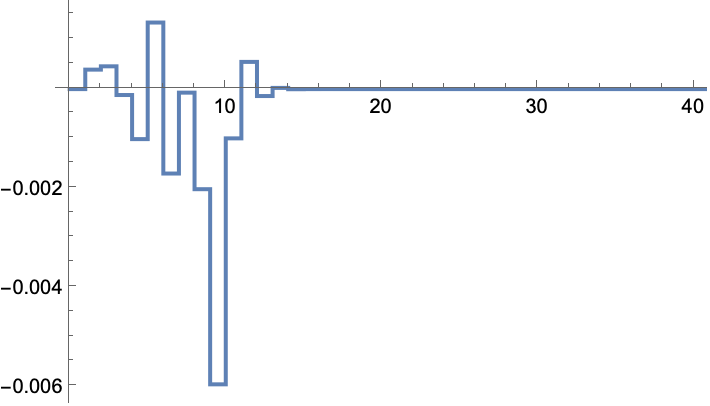
A system with a disturbance may not converge to the optimal solution:
Adjusting the initial gain may cause it to come close to the optimal solution:
The optimal solution:
The initial gain must be stabilizing:
Otherwise the state values will blow up:
The state values with a stabilizing gain:
The system must be a discrete-time system:
![ListStepPlot[cd["InputValues"] , PlotRange -> All, DataRange -> cd["SimulationRange"], PlotStyle -> ColorData[97, 3]]](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/5090d33875e386b2.png)
![sys = {Function[{x, u, k}, {0.7 u[[1]] + 0.07 u[[2]] - 0.07 x[[2]], u[[1]] + x[[1]] - 0.8 x[[2]]}], RandomReal[{-10, 10}, 2]};](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/3b34e251fae61ae1.png)
![sys = {StateSpaceModel[{{{0, 1.}, {-0.26, -1.}}, {{0}, {1.}}, {{0, 0.26}}, {{0}}}, SamplingPeriod -> 1, SystemsModelLabels -> None], RandomReal[{-1, 1}, 2]};](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/705b2e9eeea82443.png)


![ssm = StateSpaceModel[
TransferFunctionModel[{{{(-0.0184) (0.0068 + s)}}, s (0.0063 + s) (0.2647 + s)}, s], StateSpaceRealization -> "ObservableCompanion"]](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/5ff97c92cf6ed1db.png)
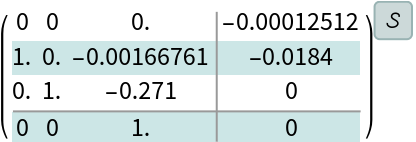
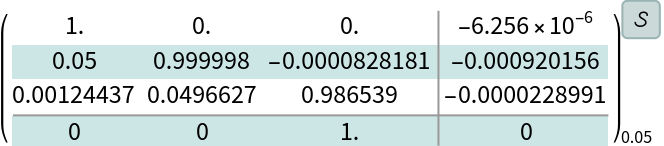
![cd = ResourceFunction[
"QLearningLQRegulator"][{ssmd, {0, 0, 5 °}}, {DiagonalMatrix[{1, 1, 10^5}], {{10^3}}, {{-50, 0, 0}}}, 400]](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/3a1563f69663d753.png)
![ListStepPlot[cd["StateValues"][[3]]/Degree, PlotRange -> All, AxesOrigin -> {0, 0}, DataRange -> cd["SimulationRange"] 0.05]](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/099f5aa5060ef11b.png)
![sys = {Function[{x, u, k}, 3 x + u], {RandomReal[{-2, 2}]}};
{q, r} = {{{1}}, {{1}}};
tspec = 100;](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/7214bb07bf8e362d.png)
![sys = {Function[{x, u, k}, -0.9 x + 2 u + 0.01 RandomReal[]], {1}};
{q, r} = {{{1}}, {{1}}};
tspec = 100;](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/660bc1fdf59e7ca8.png)
![sys = {Function[{x, u, k}, -0.9 x + 2 u ], {1}};
{q, r} = {{{1}}, {{1}}};
tspec = 100;](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/775d7263a21fab87.png)


![ResourceFunction["QLearningLQRegulator"][
StateSpaceModel[{{{0}}, {{1}}}, SamplingPeriod -> None], {{{1}}, {{1}}, {{0}}}, 50]](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/1e2ff081f31a550e.png)
![ResourceFunction["QLearningLQRegulator"][
StateSpaceModel[{{{0}}, {{1}}}, SamplingPeriod -> 1], {{{1}}, {{1}}, {{0}}}, 50]](https://www.wolframcloud.com/obj/resourcesystem/images/903/903a3bac-e8c8-4705-a916-fcc45a653a9e/63061cf32263709d.png)