Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PursuitCurvePlot

Source Notebook

Plot a predator-prey pursuit curve

Contributed by: Wolfram Staff (original content by Michael Trott)

ResourceFunction["PursuitCurvePlot"][c,p,{t,t0,tf}]

plots the pursuit curve of a predator starting at a point p, moving in the direction of the current position of the prey, following a path c from time t0 to time tf.

Details and Options

ResourceFunction["PursuitCurvePlot"] has the same options as ParametricPlot and NDSolve, with the addition of "PursuitCurveDataFunction".
Possible settings for "PursuitCurveDataFunction" are:
"DirectionOfMotion"plot vectors in the directions of motion of the predator and the prey
"PredatorPreyVectorSet"plot a set of vectors from the predator to the prey as the curve evolves
The prey moves along a prescribed curve and the predator describes a pursuit curve, moving always in the direction of the prey with constant speed. If a third argument is not given, the predator and prey are taken to move at the same speed.
Let α=(x,y) and β=(f,g), and assume α is the pursuit curve of β. Then the statement that the predator and prey move at constant speed implies that x'2+y'2=k2(f'2+g'2). The statement that the predator always moves toward the current position of the prey is equivalent to x'(y-g)-y'(x-f)=0.
Integration stops when the distance between predator and prey is less than 10-3.
Pursuit curves were considered in general by Pierre Bouguer in 1732, and by George Boole.

Examples

Basic Examples (4) 

Plot the pursuit curve for linear motion with unit speed:

In[1]:=
ResourceFunction["PursuitCurvePlot"][{0, t}, {10, 10}, {t, 0., 9}, PlotRange -> {{-.5, 14}, {0, 22}}]
Out[1]=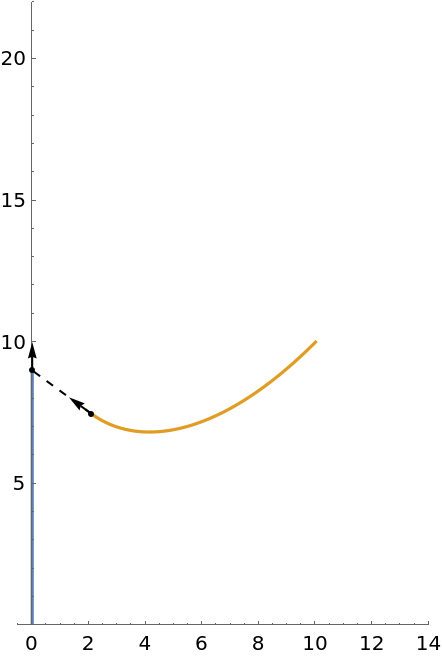

Animate the pursuit curve over time:

In[2]:=
Animate[ResourceFunction[ "PursuitCurvePlot"][{0, t}, {10, 10}, {t, 0., n}, PlotRange -> {{-.5, 14}, {0, 22}}], {{n, 1}, 1, 21, .1}]
Out[2]=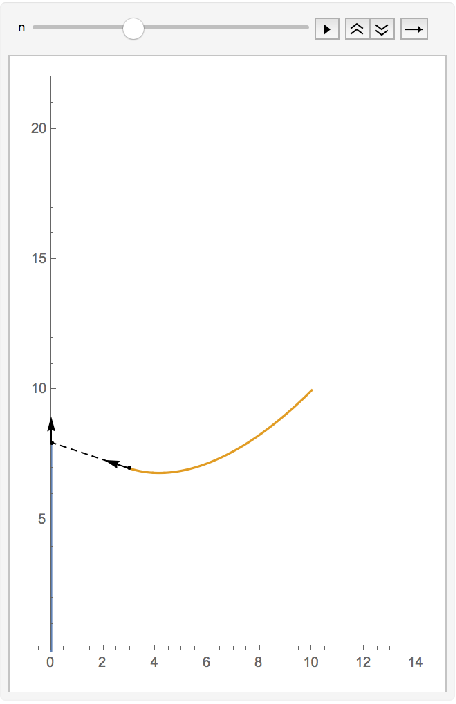

Plot the pursuit curve for circular motion:

In[3]:=
ResourceFunction[ "PursuitCurvePlot"][{Cos[t], Sin[t]}, {10, 10}, {t, 0., 10.}]
Out[3]=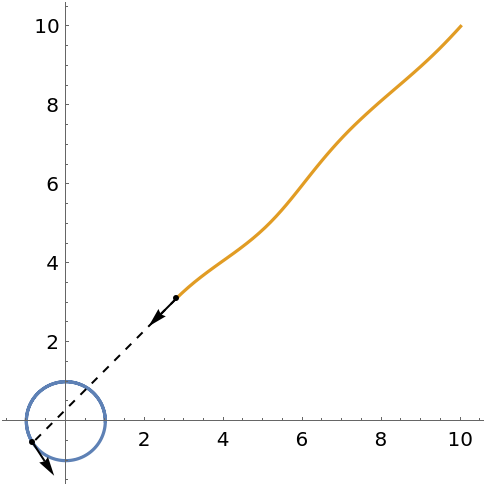

Manipulate the curve evolution via the time parameter:

In[4]:=
Manipulate[ ResourceFunction[ "PursuitCurvePlot"][{Cos[t], Sin[t]}, {10, 10}, {0, 1}, {t, 0., tf}, PlotRange -> {{-2., 10.`}, {-2., 10.`}}], {{tf, 12}, 0.1, 15}]
Out[4]=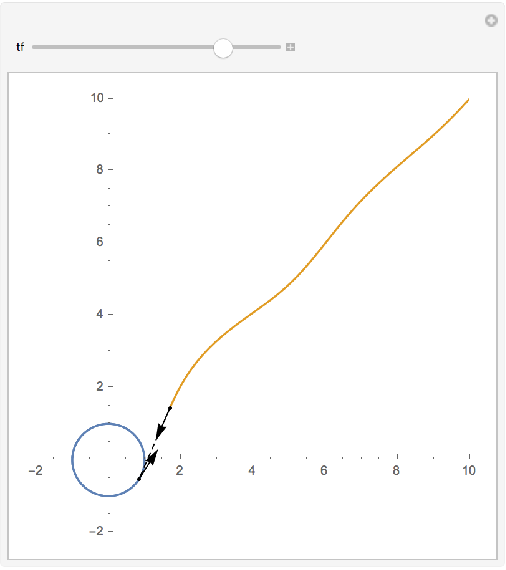

A case where the predator never reaches the prey:

In[5]:=
ResourceFunction[ "PursuitCurvePlot"][{Cos[t], Sin[t]}, {-7., 1.}, {t, 0., 500.}, "PursuitCurveDataFunction" -> ({PointSize[0.03`], MapThread[{#2, Point[#1]} &, {#3, {Red, Blue}}]} &)]
Out[5]=

Use a figure-eight prey curve:

In[6]:=
Manipulate[ ResourceFunction["PursuitCurvePlot"][{Cos[5 t], Cos[5 t] Sin[5 t]}, xy0, {t, 0., tf}, PlotRange -> 3], {{xy0, {-0.8, 0.2}, "initial position predator"}, {-3, -3}, {3, 3}}, {{tf, 29.5}, .1, 60}, ControlPlacement -> Top]
Out[6]=

Options (3) 

ColorFunction (1) 

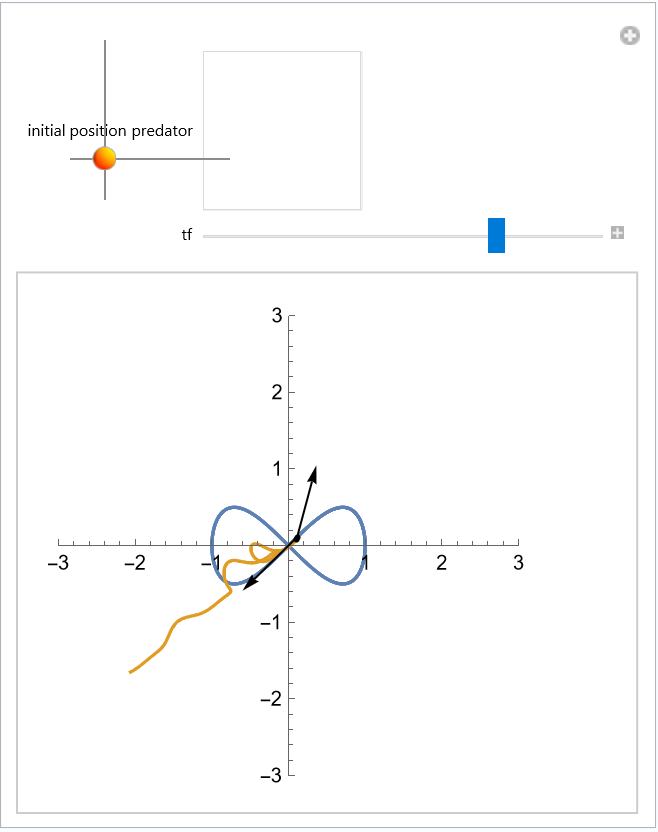Use a gradient of colors for the curve:

In[7]:=
ResourceFunction[ "PursuitCurvePlot"][{Cos[t], Sin[t]}, {10, 10}, {t, 0., 10.}, ColorFunction -> ColorData["BlueGreenYellow"]]
Out[7]=

PursuitCurveDataFunction (2) 

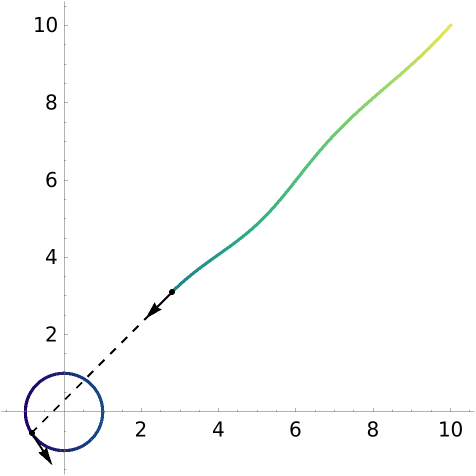Remove the vectors:

In[8]:=
ResourceFunction[ "PursuitCurvePlot"][{Cos[t], Sin[t]}, {10, 10}, {t, 0., 15.}, "PursuitCurveDataFunction" -> None, Axes -> False]
Out[8]=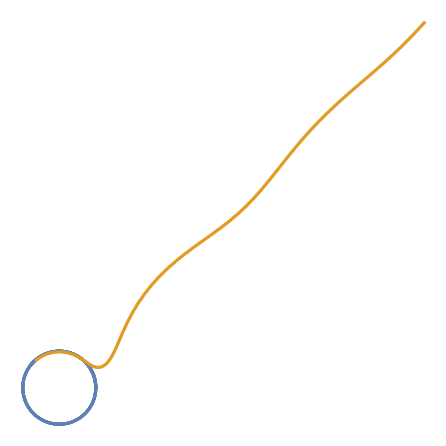

Use a custom function to put points for current positions:

In[9]:=
ResourceFunction[ "PursuitCurvePlot"][{Cos[t], Sin[t]}, {10, 10}, {t, 0., 12.}, "PursuitCurveDataFunction" -> ({PointSize[.03], MapThread[{#2, Point[#1]} &, {#3, {Red, Blue}}]} &)]
Out[9]=

Neat Examples (2) 

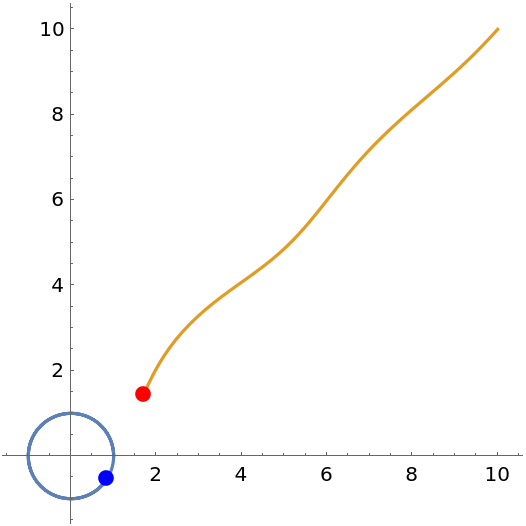Include a plot of the distance between predator and prey:

In[10]:=
Module[{\[Alpha] = 0.014}, ResourceFunction[ "PursuitCurvePlot"][{Cos[t], Cos[t] Sin[t]}, {2.2, -2.7}, {\[Alpha], 0.646}, {t, 0., 23.}, Axes -> False, PlotRange -> {{-1., 1.}, {-1.4, .6}}, "PursuitCurveDataFunction" -> (Inset[(plot = Plot[Evaluate[ Norm[{(1 - \[Alpha] t) Cos[t] - x[t], (1 - \[Alpha] t) Cos[t] Sin[t] - y[t]}] /. #1[[ 1]]], {t, 0, #2}, PlotLabel -> Row[{"t", #2}, "="], PlotRange -> {Automatic, {0, 1.1}}, AxesOrigin -> {0, 0}]), {-.8, -1.1}, {.3, .3}] &)]]
Out[10]=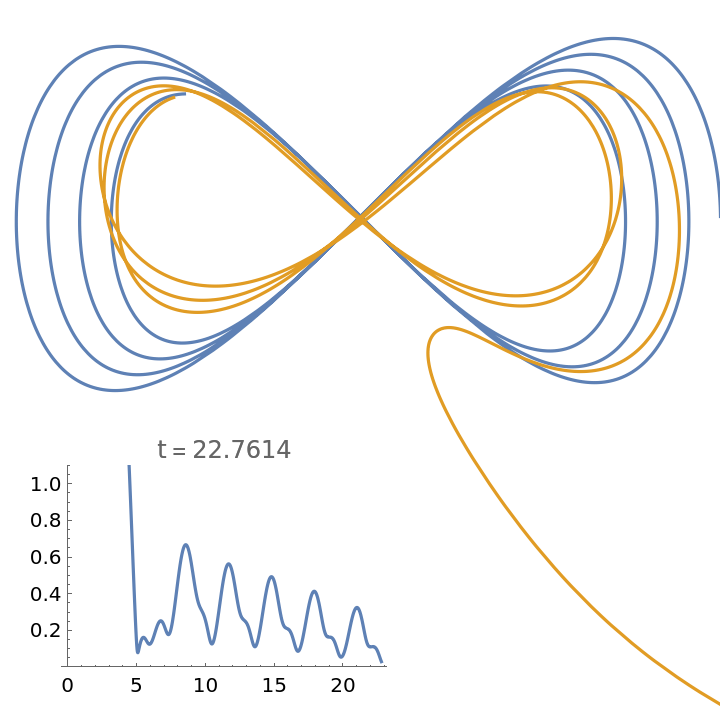

Plot a set of vectors between the predator and the prey along the evolution of the curves:

In[11]:=
Module[{tf = 24, xy0 = {2.2, -2.7}, \[Alpha] = 0.014, \[Beta] = 0.646}, ResourceFunction[ "PursuitCurvePlot"][{Cos[t], Cos[t] Sin[t]}, {1.8, -2.}, {\[Alpha], \[Beta]}, {t, 0, tf}, "PursuitCurveDataFunction" -> "PredatorPreyVectors", Axes -> False, PlotRange -> All]]
Out[11]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 19 July 2021

Source Metadata

  • Citation:
    • Abbena, E., Salamon, S., Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 3rd ed. Boca Raton, FL: Chapman & Hall/CRC, 2006.

License Information