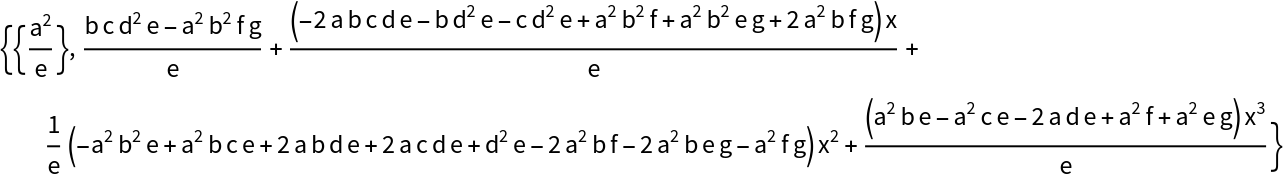Function Repository Resource:

PseudoQuotientRemainder

Compute the pseudoquotient and pseudoremainder with respect to a given variable for a pair of polynomials

Contributed by: Daniel Lichtblau

ResourceFunction["PseudoQuotientRemainder"][p,q,x]

performs pseudodivision of p by q with respect to the variable x.

Details and Options

ResourceFunction["PseudoQuotientRemainder"] performs the operation of pseudodivision, which is a form of polynomial division that uses cross-multiplication by leading coefficients to avoid actual division in the coefficient arithmetic.

The input polynomials need not be univariate and in common usage are multivariate. Coefficients of the polynomials in the main variable are themselves polynomials in the remaining variables. ResourceFunction["PseudoQuotientRemainder"] avoids dividing by coefficient polynomials.

Pseudodivision is typically used as a step in forming what are called triangular sets for a system of n multivariate polynomials in n variables.

A pseudodivision of polynomials p and q returns a triple {pre,quot,rem} satisfying the relation pre·p=quot·q+rem.

The prefactor returned by ResourceFunction["PseudoQuotientRemainder"] is a power of the leading coefficient of the divisor polynomial, where all coefficients are taken with respect to the specified variable. The power is at most one more than the difference in degrees of the input polynomials with respect to that variable.

With the option Modulus→n, the pseudodivision is performed modulo n for computing over a prime field.

Examples

Basic Examples (2)

Create dividend and divisor polynomials and pseudodivide with respect to the variable x₂:

In[1]:=

$poly = Subscript[x, 1]^2 Subscript[x, 2]^3 - Subscript[x, 2]; divisor = Subscript[x, 1]^3 Subscript[x, 2] - 2; {prefactor, quo, rem} = ResourceFunction["PseudoQuotientRemainder"][poly, divisor, Subscript[ x, 2]]$

Out[1]=

Check the result:

In[2]:=

Out[2]=

Scope (2)

The input polynomials can be univariate:

In[3]:=

$p = (x - 1)*(x - 5)*(x - 8); q = (x - 2)*(x - 5)^2; {prefactor, quo, rem} = ResourceFunction["PseudoQuotientRemainder"][p, q, x]$

Out[3]=

Check the result:

In[4]:=

Out[4]=

The coefficients in the resulting pseudoquotient and pseudoremainder are grouped with respect to powers of the specified variable:

In[5]:=

Out[5]=

Options (1)

Perform pseudodivision modulo 13:

In[6]:=

$p = (x - 11)*(x - 15)*(x - 18); q = (x - 12)*(x - 15)^2; {prefactor, quo, rem} = ResourceFunction["PseudoQuotientRemainder"][p, q, x, Modulus -> 13]$

Out[6]=

Properties and Relations (2)

Take the pseudoquotient and pseudoremainder of a pair of univariate polynomials:

In[7]:=

$p = (x - 1)*(x - 5)*(x - 8); q = (x - 2)*(x - 5)^2; {prefactor, quo, rem} = ResourceFunction["PseudoQuotientRemainder"][p, q, x]$

Out[7]=

Iterate, using q and rem:

In[8]:=

Out[8]=

The pseudoremainder is now an integer multiple of the greatest common divisor of p and q:

In[9]:=

Out[9]=

Iterate again and the pseudoremainder will be zero:

In[10]:=

Out[10]=

Expand the input polynomials:

In[11]:=

Out[11]=

The collection of inputs and pseudoremainders is in fact the polynomial remainder sequence, which can be also computed using SubresultantPolynomialRemainders:

In[12]:=