Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the projection matrix for a given vector space
ResourceFunction["ProjectionMatrix"][A] returns the projection matrix onto the column space (range) of an m×n matrix A, with m≥n. | |
ResourceFunction["ProjectionMatrix"][A,W] returns the projection matrix onto the column space (range) of A with a specified metric W. |
Compute the projection matrix onto the column space of a matrix:
| In[1]:= | ![ResourceFunction["ProjectionMatrix"][({
{1, 4},
{2, 5},
{3, 6}
})]](https://www.wolframcloud.com/obj/resourcesystem/images/a4a/a4a93b09-d43b-452a-ace2-013eec12ebc3/30e484eabd8fa63c.png) |
| Out[1]= |
Project a vector onto this vector space:
| In[2]:= | ![ResourceFunction["ProjectionMatrix"][({
{1, 4},
{2, 5},
{3, 6}
})] . {3, -4, 5}](https://www.wolframcloud.com/obj/resourcesystem/images/a4a/a4a93b09-d43b-452a-ace2-013eec12ebc3/0f521e9e9fab1d7c.png) |
| Out[2]= |
Visualize:
| In[3]:= | ![With[{A = ({
{1, 4},
{2, 5},
{3, 6}
}), x = {3, -4, 5}}, Graphics3D[{{InfinitePlane[Transpose@A] (* column space of A *)}, {Arrow[{{0, 0, 0}, x}] (* the vector x *) }, {Arrow[{{0, 0, 0}, ResourceFunction["ProjectionMatrix"][A] . x}] (* projection of x *)}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a4a/a4a93b09-d43b-452a-ace2-013eec12ebc3/58e611b345f2a124.png) |
| Out[3]= | 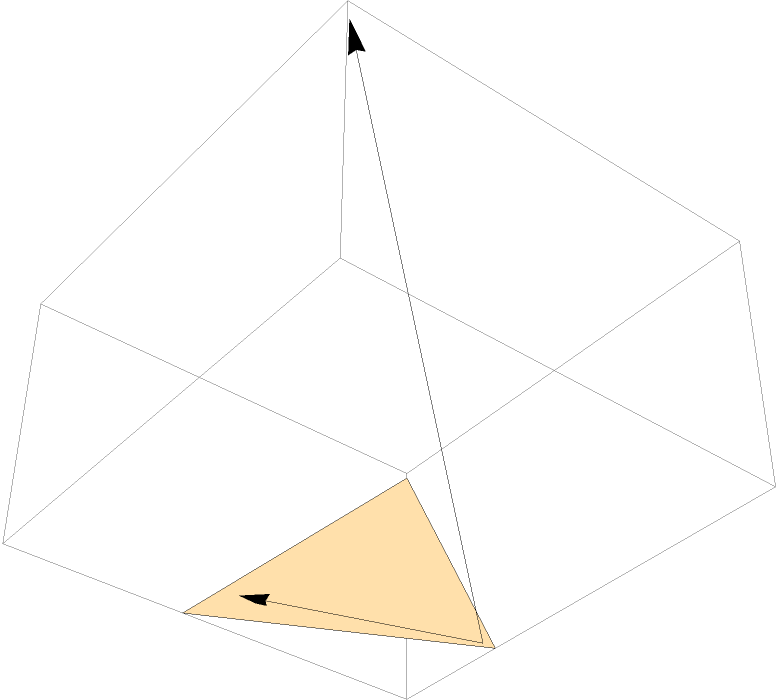 |
Compute the projection matrix for the case when the dot product between a pair of vectors x and y is given by xT.W.y:
| In[4]:= | ![ResourceFunction["ProjectionMatrix"][({
{1, 4},
{2, 5},
{3, 6}
}), ({
{1, -1/2, 0},
{-1/2, 1, 0},
{0, 0, 1}
})]](https://www.wolframcloud.com/obj/resourcesystem/images/a4a/a4a93b09-d43b-452a-ace2-013eec12ebc3/32801b8fdc0aad28.png) |
| Out[4]= |
Compute the projection matrix onto the column space of a singular square matrix:
| In[5]:= |
| Out[5]= |
Compute the projection matrix onto the column space of a symbolic real-valued matrix:
| In[6]:= | ![Simplify[ResourceFunction["ProjectionMatrix"][({
{a},
{b},
{c}
})], {a, b, c} \[Element] Reals]](https://www.wolframcloud.com/obj/resourcesystem/images/a4a/a4a93b09-d43b-452a-ace2-013eec12ebc3/5f7fc8472ec1a629.png) |
| Out[6]= |
ProjectionMatrix[Transpose@{v}].u is equivalent to Projection[u,v]:
| In[7]:= |
| Out[7]= |
ProjectionMatrix[Transpose@{v},W].u is equivalent to ![]() :
:
| In[8]:= | ![With[{u = {1, 2, 3}, v = {4, 5, 6}, W = ({
{1, -1/2, 0},
{-1/2, 1, 0},
{0, 0, 1}
})}, {ResourceFunction["ProjectionMatrix"][Transpose@{v}, W] . u, Projection[u, v, Function[{x, y}, x . W . y]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/a4a/a4a93b09-d43b-452a-ace2-013eec12ebc3/7897fa4f39b787ae.png) |
| Out[8]= |
ProjectionMatrix can fail with badly conditioned numerical matrices. Consider Läuchli’s example. The output of the function may differ depending on whether the input is given in exact numbers or in MachinePrecision numbers:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= | 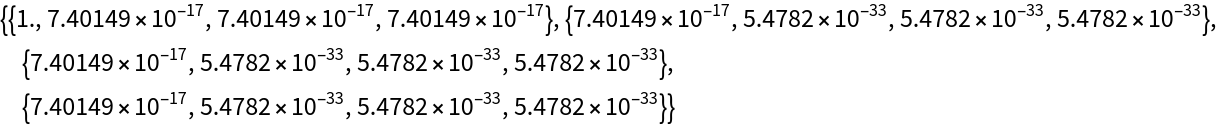 |
This work is licensed under a Creative Commons Attribution 4.0 International License