Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Project 3D graphics onto a plane
ResourceFunction["ProjectGraphics3D"][graphics3D,p] projects an image of graphics3D onto a plane through point p and perpendicular to the line from the center of the graphics3D to p. | |
ResourceFunction["ProjectGraphics3D"][graphics3D,{e1,e2},p] projects an image of graphics3D onto a plane with basis vectors {e1, e2} at p, along the line from the origin to p. | |
ResourceFunction["ProjectGraphics3D"][graphics3D,{e1,e2},p,center] projects along the line from center to p, as seen from Infinity. |
Project a curve onto a plane:
| In[1]:= | ![ResourceFunction["ProjectGraphics3D"][\!\(\*
Graphics3DBox[{{{}, {},
TagBox[
{RGBColor[0.368417, 0.506779, 0.709798], AbsoluteThickness[2], Line3DBox[CompressedData["
1:eJw1m3k0Ve/3x0lFNJFKSYjQQINSUjYqRZQSKkOG0kyjJhRCg8pcJGOUeShD
yCZjg3kMGe5w7uVyT4VC6Pt8fmv9/OGu9br3nmfv5zz7vff7WOTtnQ+dnCYg
IGBMfgmR199FojXMzR7aNf/3GqCd8++/HxqeZbcOLQs6DrWGK5YtCXKG6Rqi
0hOEXwp5t6sp0BkoHX2qLPAO5OZeOP+DcO3n6utnpV2Ho9+W6NKpvvDSSnW4
k/C7iSW3YsnnVu2ZEjwZ+BTyeo2zSgh/0LlCLLzAC+ZtdBWyKQgC9b7mhEjC
V1z0EOsi368RfW3ikvoMzo5X118hXMYj+qsp+f4a+aFB64Ao0K3X/DKTcD/n
5jrdjwHgZcmsDCyJgeOyVWFlUzR0CAydNiPX7ZRrP3AyPw7W3P8beYtwT96+
nAvkug+GjVprkl+DUtAL49pJGjR2zzlsRq47r8hylvvjdHCavV5beoKG2vSh
iOXl0ZB6MIVX9zEDys4YlIX/pUF4puTtJ2S9Xz9zPBqKMqH5z1cPCcJvBm0U
siPrhS0qYEfnvAX2urC4/jGyrrfgo89kPbNjfYUH4nNhF8vaZ8cfGjbj+Ieb
ZL19yRqnZN0Rcp4+pi/8oKHviHl15a4McIuel2O1vRheFYz9u0jTcPjY8ooa
Esfxvsv9Ye+LwaS33PA8n4b4MGOrOhKHe/J5QebbEthc5ea/b4AG1IkpjiRx
KPIehMa+LoV1qY3MFA4N1qG+z41JHIe1s0UvPKqEYzX3eeOdNGxdmLhLhsQR
fcuqpEenFrR9Pg5WlNCgt2pYcWJaMSSdqHwbVF4Lx26PnX2NNES3rlzA1i8G
17atSuIr68DQ/FKj+wcaZh1+wnpTUwzWSjNmnU6sg60Bkacl3tMwocLV+v29
BDLy1maqZdaDye7O7K/pNLD055SH/i0FjyZ+/PfCRuhKqbvy5AX5fIZh86mN
VbBffLFA3sdWkJXhlO07T4N34YfdorvrQOPbu8xzN7pB5rv6uZ5ffBB9zN/6
06EO7j7J9pme0Q0FVqVhX/l8kLcqWdjkWQf2+kPoxukG/UJ/8cx+Pvh1ul94
XFwHrC1/dETW9EAk/a/HnsEH16gfH6q16mGf4rqotuc9cC3IYtnZej44Ur2r
3Tc0gIm02IDFpV7wir48LJzGB2GbJxmnlzTBNRcP7YULmWCZMSD6wI4PuddL
NxV+awX2j0t2/fIULPWNnEdlDoJS8vLavQNd4ON1e4QrwYPlDO1j+6cPwGfH
UK+Zot1Q612xelSRB34h+YclJ3hwd+uQS4FyN8z7eqeYq8GD0Kb4sw1DPMj5
3T4q6tANV8TOFV44xgPrmct/aTB5kLTY8Q58I/nvnaqcHs0DnbkWmTElPNC+
wXz9164HVN98XGe+cgDOjm6fKeDGg/usVoVNBr2wc1zi+QypQXA0T1f+OdgP
fxtXc9wteiHsbMqBZUqDUKn4dwey+mGf+PGKspO9cHP0i6LEpkHomnQv8u7o
B7HUQ1W6nr0gu6KUG35gECykw0QmqvpBInXmWYGCXlLnRcqy3oPg4Oci+iSu
H1YLaSf4rWGAUaCmO7tvEH78+rzI0KIfWNS3o+UiTNAserpxVjgfGJ/nmWx+
3wf6zvDdk+xv6puHJ3Ti+LAzZL1YaXof3BPwyNBaQfaden37aAof2k1/uxgm
9MFS9SXborSYMBjxavOGIj48jC8+ox/UB9McTnqqOjEhSTaWfa2HD/l0y+Sv
831QkeK24UQDE5RkVP4ZydLwc5rBTznZPhjZcem54jMWuOgp35/ypsGiELp7
3Lmw/fQsOf04FjDWuu93eETDli8J+xOvckHHuTLEPp0Fyt3fFyb60zA/dGnh
ubNccK2oBb9KFhi3LwtqDadhsFnzRZcZF/SfSGjF/mHBkpRZRZhKw4cwhUzX
tVyQe/dwW4s5G+6dPjGYV01DhnSLS0QbB5Jst+vF27PhkfHxsDX1NMzcLjM6
o4YDu6TEZzk7seG+ab3gnSYaTNxso8+UcmB2wtOqX95sCJFU/lvZTuqZb3BR
No0DCR9kivLfsUHVKlGLwSY6eG/KfLcXB+SFkwQNxSnQWOn7fvNvGjKFDJ+6
riWfz0w3ey9DwVSIwsl6ol85A7H1kXIc2O6ou3fFagrsf9ms3Uv0DgxaTuVL
cmDVzbzxHj1yncmlwpVEHwNjfV9+n6BATOvWW40DFLw+k7+4lujsx7ncnewf
FKysuzvhbUne19XQziK6fOALZx/FokAuZtUG8asUlOxorppFdN9nWdSTpq8U
vJDOXWh8l4LhwXNr3Ak3PbW3rqSYgifc466efhS8kquIria88PxVjzfvKOCa
RtplPqdgl8J9lVHCB8qj4++/oWDRQ37Jt1cUTO+9+3GS8B7aSMc+goKZYTVh
fzNIPMxEpy7CHQ3HD2/2p0DxUhF70QcK7pgoq4YTvmzxWo7gPQpOURC75hMF
R/h7ptYTfu7GqfHK6xQYZbZ80WymQFjWmxFL+pDHRfVA33MUtDmLHNftpYDX
69lOk3wP9khl6RynICzB6ojeIAXBDfM4iwn384m1HjpEQdrCYOf1MzgQkEXp
jo3T4I8tJ3dvI4tqY23hJg5oiukrCo7QcC3/eWSECIkv+7r6Ux0OeDwyYSsN
0dAfd/rOigk2rExp7D1mxIHoq1aVyj9p6D1/TSSWZsPcbR3zuxw4UHC+/U8+
6R9ave/kn7SwwTvg6NGgQA78+HvGTJlBw9lN21uWvmKD4baDb9dFcsC32eS0
UjcNkooWNk7P2NC3p297eSIH3uzb/1aA9JXY94XJBQ/Z8EQjsr6jmAMj77UF
9jTTYCsqHr/zEhu4J4Ve5fA5cNRJilpaQc5tJ+PGLG02VDHcReUMuCBSWTjI
jCZ9IlyB6dzCgrErlZuTR7kgEKowoqBFw/G/OXM+TmPBJZc8hc1CfbCobh0n
V50G7lfxTcEjTMi4O0cmb04fhAQeVFy1loY7dn7VtlwmNNhuUkpc0QfcgIiY
uGX/9deA033VTNDrW6S7xagPJqzVXo795cPaTdMT8p4zwf5UrKRgZB/8zdn8
YcM7Plg2fnM9pMqE/d9ar23Z3g9qe6a9kBbjw/yO3R2PDzEgeRG35pk9Dw42
91Q+NxsA9aydK8Yf90DhP0vZ92d5MNUlmNGnPwDf5Oen3rnbA4EngqobL/Ng
7obF22S3DsDS+mxNwSs9kLfPRWvEk+h+we0LW5cOwK+tL0+OWvSAxv6HStxY
HqQNu3IVv/NgzpiXQ658D2Q6rHzk18sD6fhOGLLmQfcK6YyR092wJPTwhY9H
B6AKC3c17uuHDF5UunXad/Axw9/umwch+EDidbtODlwJom7OU2yHM55nusfS
+SDC42t+I3q/uc/z9DHFBujKWuZwi+TfxJtnL76vFyIEWVeqZjSAy5Zqg6E8
PlCS5xy2ru8Fnv8e4Y2cengSkadVU8IHLxsHK9PxHvh15gLrT2I9dO9RCFJp
5EPHfvGFxWRf2M+ajA6sq4dZk/XyTsN8CHu26aEU6W8r5z13V9ck/T45Im3z
BhqMdBeOHu/ogCdpXTgn+CtYrnPedy+IBuWHUmZprk1g/Efj5/zSMvhpELtm
VigN+aYagZd1mwAkPYMdvctg74CAt89zGoREiu8qzGwC8cDfprl7ymBwATP6
7EsazqsYHDZ62ghyd1TsDb+WwsjdeRfaEmj4Ou2OSHF0A/S4P7DY2vwRKgwD
OwzyaLjcl3DDjswRKBF7X4cqhk2yQsF3yfne06iWuZ37CTYkn3/eIJoPa05v
C13QSsOtQ75Lay98Atdz54Tdn7yH3CCZaVFtNIQ8+q1vMFQFVvknjytIvIeM
WxcXRnWQ8915qPD3ZCWIS7XoWC3Jg+JV5+V29dJg3niFpSdRAff93go/VM6B
dxpV7vI8sg/WOz7P3PIRhEOXhNN6WeD1zXdoG6nnpc3PDxoVlEB6V8ydPRWZ
sOgH96vRIA23p+/8dRdK4MPbbpUXBpmQpeeXcpTMm7fPP7V4v6cYjDwO7dAw
yYBvjxOkpIiOrJ+y1eKkFYKx5AErt/wUcr5DrioT3T/jaLObx30H7sHjJ08O
vgK/6b0mTYTfalrHCWt/C2dcggqcuuLg+5vWTTeIfiVnN+hu/JoFZ9YYu1+u
jYV1fPEF8aRPDEabdiumk/lXccvts5nRMPnmoGIQ0cEAh1W9J7lvYLHJ3T0G
/c9hv7y75ijhs6YWS8d8ToCkbmvHBV9DYeL9WrPD/+ms81TJx5RXUCIuLtea
GgwaLslRPwnvL+W1fLwYDe/1z5UZX/KHfzcP1Gwkem0394WoUXwEmBlGFQkl
+EGqjYzQOcLnS6fr/Tr9HEzni/AcztyH+B3j7sWE73r79Smj+yk0+QXXy/fc
gT/bf5Z/J5ybgqqvHX0heNB2c7HjddipzJD4RbjwvHUL4trd4PwibfGM9guQ
ZFh58r9+U62hFJpSewZUjvikp9UeheGbL4v+82EDluK9C9aaoHH6smmSa3Uw
ZPYJmTHCFdo1sjomr6L2hhsaPZMnMLlrmWcf4a8eSTobj3rip/wrZcdGL+OE
ydeBOsKHJKsLnl16hE+XWkgXX7qNv/fetE4nfM32J5F2IwEYsyqp+8mIB6av
V226R/iTo+5bmRtC8WHT4OutG32w+/eQycH/+qLb5/59TuHIW7Jeo9PpIcZd
/G1VS/bzyNrkz8evxGBie+3PGVcD8OORaSXHyX1Z7XHyVnN/Ik75Rcr8HgjD
yAans4Ok3zu0l8tfFEnBmjptF3mxCHy6+83Sy4Sfibl5mLcyDecI/fqxa1Uk
7hub629LzoN2VS1/+/pM1Jor+ztvYwxe/SDRWD9Kw/5NEg/bz2Tjmd5jKYlO
8aga48Se8YsGua9xaXvbPuDIhyJPC3YqJv+xF59O+ty/g6oqfuwiNA9reik6
nIZ2Wbf3jJFzPrTu3O+UX4imwkLexwQzkN60t7GK1MUhoYgBnZklWIpCpn/m
ZWLNPunLE1wy/yUbfV8jW4rc5cEHfq99iweCzaVzvhM/1++wr8WoEjssN4Vz
T+Yi78LldTqk/z10Kurf8KkStZ5ssWEwczEyyPX2RzKHcQ9pG7vsrsKEKXej
Frs8zApoKEwn+nA1QcUld8cnXLejdm2K9Xu0tFtHryVz3qGnaxbNVf2Cs/FG
1GyzAhy4tMUp6yPx6wnnm2Nn1mKfp+ZZbz3EvPGTCwejaFj521JO/GAjPl04
l4+PSrHi/mwt3Z2kvnyVdptmtKMEwynt6sEvmCd9bWUw0JD0cV1YKL8ddXhJ
K5yCv2D07vVSXaS/rnP5Ma1gbQfeCStMOd76BWU9mEstNtHAVDo1Hv+mA31n
PMpebf0Vv9/LfPtdkehzR967ichOvPfc9a7N6WpMfvBHTXs6DZPX9VOdvbtQ
1blq61q3WvQIZWYdLuSDrpj7xlLpXqwoYh0YrK3HjzMYrgoSfAh0uJsx4M/C
vm1RVDqjGS0le1ZesR2Ak4W2j0y0+vFTTX8TBn9H+4yIN2qkrxn+e7xL27gf
VUMplcCM7+iYFH6UeXAABkupNInj/Tiq+eCI9dfvqChjZ7x15wDccA465OzZ
j5LXZ67vEurCheejU/2JLzJ0v/t3pLIfDx1eMuPB5S7Mb/BhTHB5wBHsObh6
Pw9X+Shcd9vfja6tAgJ1pI+Pz1NWKtYfwI65p5OO3u3BOt/7R6uP9UOyqFKi
G3sQ7SyYv64oMbCtu5SSP9gPj0qZT/1/DmLwtYmTLpsYeGzMW9B5Tz90ZzYH
eEwOorL+rqwregzs/hve/0u9H97fOJc5KcnHNzmPKmxsGFibd7ItZnY/HKy0
4Vvp8XHrPzfn3yEMdC3SD44s7AN5293mKaF8dF0yaKoynYm+gfr3lRf3gYtn
RLD2Shondk3tuN3JRI/BKQia3Qc3VzfHTK6l0Y9htre+j4kM9sLeP4J98DN+
68mwTTRu/ymVIf+HiUG7HHjJA1ygtDYPOO6k0edH3f1McRY+qJh+DUu4QP94
v+DocRrPy9EjfvosLIjYIPyM+J5BVQOJIH8aTVadur0unYXHtgyxZHI50Pfh
sfX6NhpvbPe7MMuVjeOHpqQvpnBgr9+3DN0OGlcobN1Q7cvG09N/uxbGcGBH
/7Jw9S4aY9niCY+C2MhQ21a5048D2o/EFN4zaawLKXg2msTGzsUHKmfbcWBu
e1uZ4SCNHsdXGQZ+Y6ODDv/ZenMOsBuPuNnSND7/4Kq/hs1Ge+0Pr/fv40Dm
grFc85809jiOdRb9YOOR06+f3tzMAT+niWTWMI0H3WdUNwtT+NtM8evDWRwo
S75v6zNO49svjWc+bqaweElG790pChxCk8ej/tJ4X6+Rs06XQum8WUaXhigo
qG8XDZ+gcfilUd8zIwp/rpu/Wvc78TV/Yh+sm6LRn+10zsKBwo2Wm+PkGiho
n57y+zPhh5RdqTQnCjWFlriOV1AwLzGmRf8fjRvGv3wTuEVh/6dbuTUFFGQW
zloVR/iKH0F6xt4UBryVPvKS+Jcbmx8MdhNeNyq6PNifQjWlIlvHeAq6lVgK
pP+gkf2ZM80vKKzirmxaFU6B7cfJL+OEF3zjyou/JnmtkMrmPKHAz6KN3Ua4
8PmyXXuyKJS1tJwZ7UXBnMMhl54R7ueztfb6Bwp513M/H7pBgdfOa84ahFf9
8SyKraKIbo9MF7hAwe7a1u5skpfID8a8qkYKj77eRRmYU2AwpL3UfJJGpgKn
WrCfwsh4fiBlSEGPUyTbheybdvr8zYtGKJx/J7XYDShYaqShdIPs8w37Y0OK
Ahy84ZCc9EKFguUy0mLLxmg8sen02Q2LOFjPLBIOHWeDrmS7T98vEn/Upd8z
9Dho4Wnv4PuSDU6TauURPTT+rfi7+sVzDvJjGq5VB7Ah1bzpZfl3GhfNXFZs
GsfBcacxjbk+bFi18/es2nYa07+d8piZxsHIbsH6O8R3l0y5v/FqorHr12+3
Y6UknlbHbAVgw2M5ySNXK2hUCru6sHCQg7N/C9de7GaB6f7dWS6vaGxiFbo4
6HLxxaLt8+waWOB0fO9hvSgaF6fc+hxuxEXp7/f27itngc0e66N9YTQyLCIX
frHgIi/QNXtOMguilZPjPz0hcc5a6b3IiYsHj95hGrqwYFle1FSjC40hvwSd
j4RzkX67vy9RjAVfGRXjC3Vo9B7bG+f9k4tm9/4UL9zIBDnbCYGHuXwUlPWP
dw7vw++HTq7ycuqF8visoIDtg/ijUvHjt+Z+fGBQMWJq2wtJd+VUStUGkSen
tl6sux/1u6b1yR7qhVzu19VNcoM492r38s3cflyu22+auLkXJJ013wdPH8Se
n4JXL4/3Y/3nwiTPiR5IisvOCfg8gDpy6jmBy3kotWNlx6EHxPecHPJ7YDKA
Jqqhp0+d5OFOKdlpYtANaqoN2f27eFj00fSUySAPXev2BKu7d0Ch7sbad41c
FBrr4EeyB7CdMoqpUmuC5KC/GorKTAztWkxPWvNRtPV8/6G5TaDssrnjnRgT
U14kNlk78NG3bvxm62AjjAxfKl73g4GXLOLnZJ/mozjvRkBtSiNkmxd8YeUx
UFu97IrBFT7ePyeQ4Lq6EZwMz1oeMGBgqqofNes+H22veDxsID7pzQsZaz3H
XuzvrZfhpvOxoG9mQdrCOnixfbfGLIVujC0PkJg/xkeZ2TdVLjdVgmretoNf
zrTioeKv+6su0rht73WTtyGVEDM6KmOq1oq31yau/nCFxhaXxeF880ow5Ci2
lf5qwWuV/zYmkft8LTOvzvRbBTScmhC0u92CzcPqFeddaexoX+PR/r0cWCaS
qf6PmtFqex0jyJfGq1sroyl2KZy0i3079roRx6v/WZ6JoDGvkbKsZSGUrljq
vTG+FtFIir+2mMY7aT3VixwRKA8XW8dVtThr89BCpY80vtfMdzbnFEHlkYIt
t1NrcPn9cvPFZTTe+qFRUtT3AUqFblQaZFdjwA0HeUYljbu0+udu4RdA9uUX
P3xLv+DeoevVUrU0Jmik/ekdyYULVUGDw+2VOPRUUla0k8b6ltmOUwIZMNZ6
vXrkJ+L2FwoC40S/f/c45S0QSYcPHT9n3hwrQmrydfSPHzTOWs7dqjA3DU4Y
/o7sEihC4Q9RL7uJrn+eb8deuzQFujb+izk8rxCTvGemJAzRuOaup8vPDW8A
vHwmZ6zJw63CLMlvv0l/axF40rjlNfT4TqjnbMhFtuGqoMA/RM/uCEpl7EgA
wQjzbSZbc7C2bd/5XaM0XrjadPmowStg+0tf2r37HXp531ULIDqk9mZe7RXb
aLhc2he33yYDl5y5yq8huqVu9EXM9msknBKp5tVUpeHKmw6wj+hczE2GdH1r
BGwK7lrGbEpBg7K5/Ui4asGaaVH855C59VBU/sAb1Nu91iiQ6OU615rKibFQ
cM6+keoxmoBZq88L/SC84smHuWYzQqDx4vaPG6fHo1uSkKQ+0V0huPTvt3QA
cFdJ3TomHYOto1ydDsIrl9hv8Nr/BN6e08xONI5Em6ULrJcS/RZ746gofvIh
yC5QuelxIhw1XI0biB/AcdmLlc9v+8Bu0+xJuB2KczseRnsQrjbxb5Z0oCcc
tM4S6AsIRPEqrEwknCuwMXfDQTfY0z/rrsDBx0i/Yez5TPh0QXcLJfdrMPp+
z5CEuzd25vLkmITnhre/XmN+DnZNN06TN7+NQULNh4YJ16hepSZiawFd82dF
zbQ9hUedw7//18fctg2t2pgJGHGvkrch8wCMZWmW/Ptv3R/C6QciHLAo/oCA
UcQV+Hosa5L4KBQxltq0LeYSzkXTu+tiPCCrckbQAOHU+oNH9169ic7KMgoq
Vx/AonVbPFoJ/3ZIYtObuLto7rdV416cP/DC91XlE947v1xH5fE93DGy6iLL
LxhS+wxOhxI+fHcsWcrWD23dtdY6Ho+Au3Uqb//rh/tVCkNKFf3x/SbrJTqK
0bDcSM7mL9l/s9MyYy5LAnGyODb5g1QsFFxaZ59H+Af6y766aaFY0r1pmpdg
ApyPa7kmTfi2cn0RneaX6Cmyevm0hlSQvuZa7U3OieGgq9GXT1HoojQM3eXp
ELr7yM45hPc/1L2t3B2Nevtsp2o6M0BC8Z/EY3IOizXDayIbY1G+PfKUVV0W
TL+7uvgamWsq3USemhUmYOTsyc/PcnIg9nC5GY+cf806m+XpfmnotOnn7GL3
Imh6ciPwFKmvePa3S3Uv0hEudMva+RH9WCn28TipxxFZyvmqWQbuoGZa0EbF
kLN87/B+Ur9mQT8H3E9k4lspS9h8rAS6en7bSZB5zX++1x8Lz7eoY7eWqr9S
CodG1p5T5ZJzXiE5PFqYiyF7R3d/jq2EgaRL3u+IPpSqDom4LCrGMxf7S8J5
tWCol9g7C4luLJDbHn+9CncI3vm4cnob7F6vjD9P0/hk2lH5luwq5Ow/drVV
uw0CPm2MpU7SWNIsPCowXIWK+e9tL91sA47T3MZGexovjjdt33XxE3oIGwpZ
89vgrqqW/DMrUkf5jJt3Tn/GbOmKtXNav4H1lrF7JQeIDr8LvVpg8RVNu+YZ
RsV1wJEPScsSyBy9c19airNUHUbU/CsSVOkGn/iAe+9G+XhYOUtRn92IuWd4
6f1cBuh5r5dcdpaP0z9HJW5q78DD8+m00AV9sMjKPudp7QAmq9p4PBrtwO0t
yna3VPrg1sqKxM1VA8RPzQhtX9SJsTUmSno7+kBhzeXoxuIBvMI4f9jOtBMr
Nfc/dnPsAx2Z1qg/mQP469erbfO/diKtXXEgJrcP7rZ/kOsJGsCiR+utBgq+
Y1vvw2UPDveDa9Y9wc3mA3jyIYvtENKNveEfluy6wQNFPRXHySYeBt9cn10a
2otLdmgWKTkMQoWYyewHBUSy/BXkWXG9eI1q93zoPAgpz3NO9Wb143eNDkOB
zF5sC7rfXn97ELx2CB9UT+rHbo0fn9d86cWMgOwFYsGD4KD+ubn0eT9+VDNd
eeBfL9JnpE8rlQ7CiltsxrNr/Xii7ZZXmSMDWaISn39L8+Gwxhh3jlo/Dg38
kzu8kYlLs4feZefy4VbMwV4dMs9sXDB3K6XNRJuW6xMuxXwYWK+uXOvfh5rs
hMQr+5i453BywNJPfPhhPVPXwrcPP9055n/3BBMPH+nyEmnnQ0XF67HDV/uw
zUJjsX0oEwWf0q/cx/mkH27Gmfv7sP1B7xndMSaWjm1SrN5Mw3Mwitst0Idr
/eOOWBWw8FdKu3VpCA1z19Qe07Xlom2F3w3zKhZWJHc2rX5Bw6Ngm74NZlyk
znMzDZtZOHuU4egUTUPncbOn0oZcLH2kZy9Ps7AmSqvsQRIN2vcl1NrVuVjc
+eOQ7wo2Fvwpq5j/gYbHD87OmyHMxWCVHbs33mfjd6dXPpYdNPRwB9ZKpnBQ
6Odr/a/BbAyb9VPTs4uG4qvD6c+iOXhG54aybQwbC90rC+710uC3LclNMoSD
Then3byWz0YT5hMZGQ4NwU6bZ467cTD/m+qo2QAbi278FHrxgwa5oErlawc4
6Ht9VUDRKBuFFVqbon7REJG63qp0JweNFFYPys2gUOCok/XdYRpE18eNiG7l
4CR7TU+DDIWvM0wfN/357/nNyAkfOQ6W3VE14e2ncNlDJ41PEzSEPx8KVPtJ
oWiobpS8JYX+CZsCkydpiJy2w3gvm/ijF+dCDp6isJUtF3ZmioZtIg6+lt+I
T/mwed3tKxQ+uWFpKPSPhqWnq3adrqaw+8+aM5F3KJRq3Bx/g3CnvPr7TiUU
DizqhIJHFFqnrU78RPjvk2xzp2wKp+U0p9c/o/CkSJfZb8JF357LOpVI4Qq9
pOzeOApRUSZ5ivC4nJrIYy8p9B0fMOalU1jg1/WGQbiN5S3ZPQEUxv/ceI1f
QKHLPL0DsYQ/tuncokr82vK5C1R4lRRmlfhH7iB804ETvNk3KcwTU3LoJT7J
d3L7s3ckr4WPvXZQ5yk85jpTob6bQoYdQ1OY8Ld7Uje8t6VwosrkRD6Pwur6
3b6byf4cczP/4n2Ywlcb4xRe/qEw/IrZXSD7KTc+MsdoL4XzohhzD8zjYMc6
4ibHaLgz+vdF+ToK351YuGm5NAerO3e7eY3S4Dj3KP+GAtn/2o5PlBIHn333
2zDxm5znwLA/KxdTOPi4VPOENgd1YzTf3R2i4c3b8u0XpthYd7Cyet4FDpkP
qq1a+mnIf6Y+nPGVjesfizOVPnHQcsO05zkNJN+km+vnn2ajflRp/qdGDt7f
GSZ/oJaGvPZXX7ZasbGMNk117OLgcVOL9VVfaNhiSstYmRA+8bTtyRAHeV3W
PMsyGhLDoocCt7JxW6DR1DMZLqo1jumIvqMhtu5XdokIG+VW2+s9ushFKYOn
0j6PaRA67qOm9IaFO1+eaGWK9+HLTOFLy1eR+Gd0DMkymch4pCxeLt2Hsn+r
C+rkadCcflkrvoWJSiFxktEr+3B46vyWE0tpmAx/GL7yMxPL3gg779Tsw0Ws
nC41MRqkNKOTF2cyUUrghSrY9mGeTNpHUx4fbG5rXyxxZ2Ke8PdckdQ+7N1+
eJARzwcjOR1ttSVMFPlk7tmo24+if9tPmE3nw9gTCSEvQwZq5AiFFxj2Y2b9
PS+XsUGYUEvQfruDgSpdjpdemvZjV9d1udv8QdBR/qPQvZ6BAR1d5vtP9uOW
AOl/am2D8PHyjNFVixl4jldfcuJ+P3p/u3hLL2kQ7BVuS/sxe/HGfn99++p+
tDYxX7rCYBCGFtkIeN/uxTN2E3UBh3jo/ql5ctHlAXjXKPLX5k0Pbtitu8zc
YABD7ug0lF3pB7NHLgafBr4jS8Eoc5cQH0VEpKyriK99/jG8FdVbcE9h8FCB
CB+HV9t0FOez4OMImEgvakG3ADnWmrl87E9+pRgfy4KqqCnHS6PNWNmd83lE
io/uM/a4bLjMgqTV7x7N+dCMU/6bHmxQ42Pll7cplvNZ0PGgwHWmfjM2qIqk
7LHgY+3eDksxAyaEhOpbCFo0YXXUvAF2HB/VQ4/s8krpBb6v3T/jaw1oGmt/
PFmJJn5RcVezZye8qY6rKTKoRt1P62cGrqYxM/3vjku7O0FEvYUjJlyNpwam
FTur0Xj/GdU0INwJfVXtGSZlX/Ehb8/p+Ro0zvYWGPby6wDjoprIEu2vyLwy
cp7aReMWh2vZmsHtkGgoMW2n+hf0O2NkxbKl8ZyHVrJgZBuUyU4lNS39hPNn
wwz5QOK3vKouTEY0QWX2zuX5rDLse7ZwCTeYxshk3jopqybwfh3qsCKmDM0m
b8snPKOxbva+KGlp4nfvXS6+Z12GQW9bZgu/pFElMCb9+/NGcOdpzd3aUooK
fme2Wr2m0VkltMQ8qAHE5bOkLCs/otqVHB3TfBrX5raZ2tyrg4HbOsy4N8W4
TXrokfM34tsqco8lZVaBzlhhi39tHurNfmEy2k7jxqaX8lKbqmAV16Jwm0ke
bh/pkLtJ5rKArgcFF3IqoeZ46tOuuly8bJTEsO+m8eiRGJuG/AqYrlzsLtmQ
gyvjr/S2sMi8aSSz4unHMtBfbTu2vekdLsAFnjp84j8+x3B21RRDXlKTVkRr
Bg5qhbUakPkx/Fcu++yBYrjV/YA7ZJGBEtWv1PeReTNpvc1GwRiEpax+gacZ
6fhqyYGpzb9o9FxUpTH+6gP0rqQZ5ZmpGHnCsTV5hMYbJ652+ie/h6fTVyV1
vk3EUx++nZUic/Gp66qi695lwt/7NUuonBgc0p2YG0t4+UK5T9x3GaAX7FWy
PjcaJbOf5iiQ+fqpkXKGwrl0ePPI+CbfKQo3sx7Mm0d8mPjZm2XnLiSDy5Dx
0Z/OL3DSq4jtTeb3SLnZ8qUX4+DEwhfdby4FYWC8cWwt4amGXGeHSzGQ99PM
ZtblAEzx87QTJ76h5ej0eBYzEqJnpwp9YT1Bk6mXHFfCM4obIirZoZCW5XR+
JeWDmuln0hIIX5a9/kswFQiZO/Qef6I88cJlMg0Tvv2B+IbImsdQm/yYV1/j
hovb9u5k/Pfc8BJnxkitN6QNSOybVXcN1Z2Nxf/zW7eZJ1acj70NKGt70SX2
HPqXp/X+57ckjtjsiDc4BcxBkaoEAwusOXX23X9+q885a4mhw0EcdyrTM3TQ
BdveOw/+81u3l0+aXjG/ioqfvJyvm58Av8IftjzCW1Mfcv+t8sRCL+mXYqsv
wwXP4m3NhMtZOE17p/IQq+v2jLWo3ILB/OFFuYQzk19PJiwIwJBVIVT1Ag/w
e5nUYk/4mmshX2dJhKHb/ib6nsQDeHxQN38t4e3vZ8UtFn+J36pE/VvFH8Pg
I8doPtnnFOObW6ffj0a7GX9cAu77g3J4xNVjhHu9XOJe4vMK1y4/8KvWNxie
TONoN5D7u447JabhlYKfN6afFPOJgHP2Ai9tCG9XUYmecyMNFTYp//C8HQmt
5YXGzP+eS6a2jjloZGBdb13wza3RINAQ+rqZ+KolHYLJ/NVZeOvlUtZ31Vi4
VXlXx2aURt3hKzvWLMhB+8QNuy9KJYBY1ofV/4ivSmDWrnXu/oBh892cfQdS
Id17ro0HqSNfsZDifRkVaLz+wqELlTkwyHp8QaqLxuNjWiHpayrxMag4me/K
hSc3hltek3rkuc1cM5lQiUuUdIc1S3Jhx6/2vHRS1xmNocWmL6swrjShks7P
g9w+1VKHRhrjlFwSeu9/Rspzz64Fafmw1Ob3Xuty4tvKbXSXWNbgt/yfdrJB
RRC69OmGsDgauzvuydoPN+CcBWbXP6wphXGdnFyRGBrzFaxvH9jciPmSG5L/
OpXCHNh1wDmSRmG3GEVll0YsOLTcflNWKXgP+GTLh9Fo7PtoW/CfRrysDHNC
tpaBpk3jFeknNDa+2XDdeqwJqeZru8V3l4PKQbUzDi7EX9osenV+tAXxwYwk
llUlSAoJ7t2nQ6PN6P6Fvox25JX+E7ri+wUaqh8Gvn3Px6MBg6z0Nb3or61x
bBajHkozkzx0svn4NUrs/kX9XoxIMrvpIdAA5y/MYJZn8DGl690aObtedPNq
WD2yvAEa3ZsF8l/zMbomU8yI+J5tgrRSrWUDDLipVe0J4eMnjz2mjcSvXIzb
lmXU3ACp6ft8xp34GOU/y+5BLQNDIkUfn6pshJIUs5Xly/go4Z4kz7BlYfix
mybc183A5YQv2Wo/iGWfPUXHd3PwxYfsxbeOfANGzdt1JywHkbF4msF9aw4K
njhjMvvGN8j50fDZ9/Ag9siO+P69ysHHFYmqz559g7mNC55n6w/ioOJQuH8c
Bx28bTNDW77Bd6+8iuTVg6g2/ajS5X8c1HKd3a11uB08ph/cMf3nAHZ8uF/6
N5OLV7l57EX7O6A9b6HZ1esDaJVrYnhdsB/jqvrf1Gl9B6vjg+q153hYbh57
9ceuAaz8F+Cb6d4Ddw1ubVjswEOQiGp5e3gApfdn2ik/7oGJsd4nFsd4eJX9
I8nixABukpwV/fxFD1Drpl0p2ctD/9miJ3W8BlDOx1jzQl4PsBfrrNy2kocn
js7UCcYB7K1mXOj62QMHh51sSjr7cXnNsTlbNg5iE+y3++7QCzF1ln+26vdj
8/MteyamBlFMNbxywy4GzNVWqw/Y3o9OW1y5aaJ89NpUdX32IQZktHVaMTf2
o8ghA0mdRXxsvCg5l3GcAfcmngdflO3Hm2ZL2ybX8nG5T/R3t9sMuOXgW68+
2oefF0tkso/wcdfimS+vZzHg4v10zvE3fUil2SpbJfFRpez97ouyTGh1KJO3
F+rDTUmWvc/UaXxz4HS95QgTCuxHZf3GuCiZOl3CdxuNudJ3zBIFWXD5maR4
Bs3FOvnsKQtdGuud3gj8msMCV5OQZnYHFyv3ff8ZuZ/Gl8pGxVeVWGAT+Wf1
rHdc9Dz75HHxKRqfO34NAAsWqK+fprTBgYs6NzUvGJN54aOQVh8nlwUrk4Ou
/j3CxcNbhX3M/vs7gsDAbaqUBT4Rw524n4vvb45PaZO6NI+ImtlTy4JhGfEZ
W7Zx0eryialsMi+EUVdHSzksCBS8Ndo1n4uZDYbZ6u9pPE1xJvYvZgO3ujNy
8QcOhomqXzvbQqPAOdcZztfYEB81PfdeFgen/1gd6kP0Jv5cV5G0BxvuiRwU
H3jNwbWLJL55EX3Ctef0Sv3YECMQGZoYyMG2C5vfyzNoPPI2P2LaKzasbtBb
23OKgyM4L6yfR+MBpUsH9BrYkMTEl7KkHvoraPd5ZF6YnXpcrPw7G07oSzge
PcRBPf22ywvJXEDdm3Fbr48Nrt6JMwq3c/ByqYhb2RCNJnlmZ1UFKMhZNv/z
DnEOegfb89LGaNxq7KhVqkpB1b4ILZOZxHccXifeSfR74N6JPdKaFOgYz1xi
/Zf4KeGXW/uJ3juUj/64sIuCd3XiKxyJH20Tsb+fSPr/9bM8cSFLCpbmzDC1
b6cwp0E4/b8+c3RJvdduRwrc1V3Hj9RSaPSA1zhA+CdHy/uelyjwbJGXNiyj
8OmDO7+P/9cPdeqX5btS4OP1KnfzewrpHYcXvSN8PuuW9oAvBcuvvW2QTqOw
fLmUet9/z2GZMf1SQRTYaf1zmoilMCbrmdF//TlRLmC5TiQFKgWaT1uJn/V4
8sGe+Fmc1hjcapdIgb/qIo1UP+KPzQKv1RAefG9cwv0dBXqyBo5uHhQm5W/3
9iV8n6R4TTCSfJ3vr9jrQqGSm2CgPOFWOSozEz5T4LJb1LD6OPG19l6vRsk+
LMuIZeT2UHBivEMz2JRC8wJWnQLhFkWeWfEDFDhK+1Qf3kPh+nOrH64mfVUZ
o8f9RimQXXKM/1GNQhvXidefyX1p0RKh9sznwFljhRumk2ysODI934zcx4r1
s744AQc2/qnmcn6wcZd/2jVr0j+3sQ5MKe/jgFz5+SUuLDYKNb7+okPmx4du
3Cft5hwoSsipuvOFfF71oEl4P9m35R/y1zhxYG+2auneMDbuOCgpGkb67UXP
5T1uERzo0JB9luzHxj/BiSw3cm5nvxCPEXxDruMTuEfkLvGjEeaXtMk5X+rN
fOX+lgPCnx2N0h3ZaMHhpx9qIPGHzD194jMHopgC+96ps7EziKle9ZHGztlH
Pbr+cEDtm/u+l19ZSNGx53kRZO7Ibln78CAX4tSPvohCFnJQ5s5jMu+fNNj+
LNqKC7+slk+LyGLh4sodgWLEN0ynZ4tnnOLCn3FtBa/nLNwbldH4wodGwUUW
SvluXEg4MH+Z2AkWlm5XdZvjROP+u413biVywY2xfN2McSa+Hxku0iI+ZnhS
ZkviPy4If1A9WyjPxHG7y3+mkvm4stTaMTGhDzzN+8d/SjLxwMxUlbZY4uf0
dFLVMvrg2khVzQoRJg5i3UBgGB+DbS2DUt/3gY5CgpELn4FX75YfSvXh48/q
GvXnX/vgJkNjnJXPwCP54ZEux/k4v1r0ntyvPvB9vZnHPMRAmW5VhoMYHwOt
Fx37q0X8pVJyk/udXhxYuiZ02GgQizj0r0+f+8Hncn556bNupJmUR9JNHk7f
Htdn0sSDdbmH8yuD2rDJIuuMZSaFyxxuhfQ8GoTJrrZKuSd16JQcL1P6txv9
g7T2q/XxYY7e1PAj5zrcv4Qh2F1GeOY3N71BPjicWiwzZFKHAnkt9R2Pu5FB
yckc+MkHzfeSrtkL6tDqoNHsm7LdSJnmJBwc40PvyL/HizbWoujMt817dLsw
WTz3818RGvyWpe8U0q/Glkt/zzve6cSP1LAHU4kGYeVXBhGnP+HaGCfBNZw2
3Ou6wWncioZl+pNeT1Z/wls3N9XUpLQhozPvy1JbGmbqJofeGqjCir+m149d
bsOQ1gZXdQca1qp89NC5WIWac67tXD3Zih0C71uMz9Ag9vewlPf1StyMiqJZ
4q14abH/YaVrNHTig2dT98rRPVShIVijGd95vmo7+YiGCBerNzIRJWj7Mes1
XKpHkZPrTi3NoqFwhq2ajHkJ6hi/Ed2qWo/Dd3glXu9o+Nr35dzi+SVoaSvt
Jt1Xhz8vCV5h5tCwYKaW/YRXMX6Pe9f5yrYOM/8eafYuoOHh1TKlha1FOKP9
/M6QlzV4yE/N17yMhkbuIpeQK/m42HhxnfmBz2gi1zNbuYkGvbk3rv+j3qNr
dVP5n7JPqKDR6TrSTANdQAfZHXuP3ybOHry57RMOfxXQzG+lYfmY/6e5unlo
5RZRLbeyCq3vRwYpddBwUFCuTXxuDhosu9G+YKwcv66pLX3YS0PD+cg5PQmZ
WGi77P1ykrfVscaEuwM0bGtr7ehekomlgtmuUiS/wFMKUW8HaVDwar7S7peB
+//tuzJJ8hN4dLyzk0+Dg6fEMQ92GsbIuBssJvkxMjYpSvykofKW2o9k1yTi
a3vCnpH81ncp9giP0CArfsTfzj4RK6T+5DqQPJp0gn4PEP5wmtDVeXvfYI5O
4+B8ksfkwvMHqn7TsMZB1MZsQQKa7K2bWEDySEk8XGk3SsO1xBCloMQYfG4u
ps4geZS9P/9J9i8Nv886G0k+jcYksXNhnSTeG2u9B3II7/B/91WuLxLvhDyI
9ybxXjq7y2TXBA31e8JejriH4/oO1e0ZJN4I5pxvupM0THskFdRo8Bz90rSL
F5C4fn37PJlJuKtKuHySZCgKybglHSVx8cSD7aWmaOjdGZW/MykAUysdrzwj
cemfr+dVEn5CyVBrfv8TvHo93nEVWV933vz5xN/CxiH7kKd3HqK+dc2WKbK+
7Ah9xYRwfZ0FnTMX+qDKD5HCLLKO8lfrxT6E1zVzTl1P8sB22GFmRNa5omUw
nkm4okT3ivI7t/DGUe7naHK9ccarZU2Ev0+4Zh+UdAkr02Ne3iffC7R0dB8g
fGvEhTt5SXa4e5dKTTZ5/5eGj+xfwlduePzf/8cVTa7/7zWg6P//P+5/5Q+U
dA==
"]]},
Annotation[#, "Charting`Private`Tag$87157#1"]& ]}, {}},
Axes->True,
DisplayFunction->Identity,
FaceGridsStyle->Automatic,
ImagePadding->Automatic,
Method->{"DefaultGraphicsInteraction" -> {"Version" -> 1.2, "TrackMousePosition" -> {True, False}, "Effects" -> {"Highlight" -> {"ratio" -> 2}, "HighlightPoint" -> {"ratio" -> 2}, "Droplines" -> {"freeformCursorMode" -> True, "placement" -> {"x" -> "All", "y" -> "None"}}}}},
PlotRange->{{-0.9999998592131705, 0.9999998782112116}, {-0.9999996658276197, 0.9999993650500513}, {-0.9999998830731719, 0.9999999999999918}},
PlotRangePadding->{{
Scaled[0.05],
Scaled[0.05]}, {
Scaled[0.05],
Scaled[0.05]}, {
Scaled[0.05],
Scaled[0.05]}},
Ticks->{Automatic, Automatic, Automatic}]\), {0, 1, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/3c47a8b5e547b466.png) |
| Out[1]= | 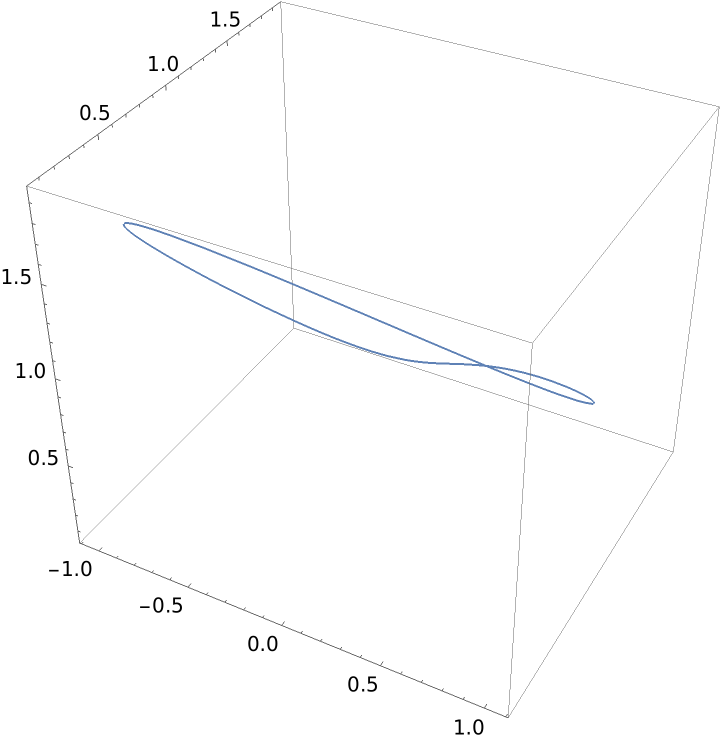 |
Project a polyhedron:
| In[2]:= |
| Out[2]= | 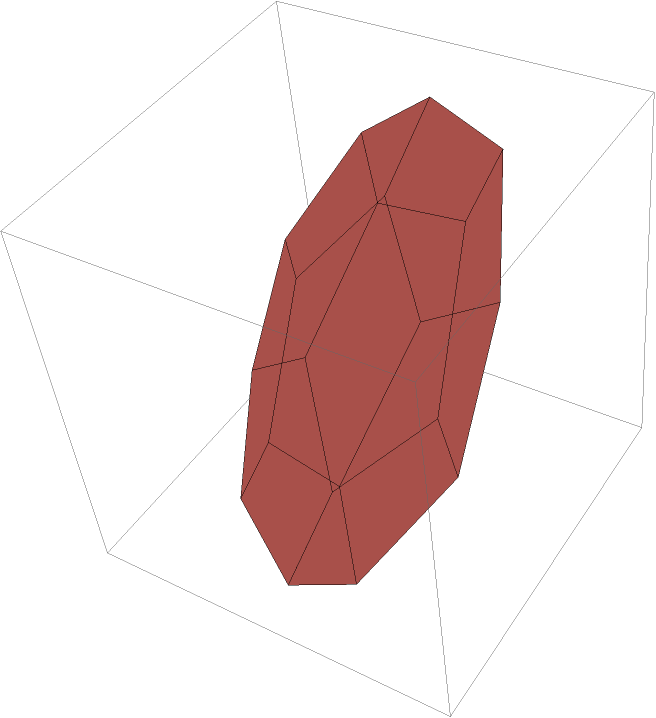 |
Project a surface:
| In[3]:= |
| Out[3]= | 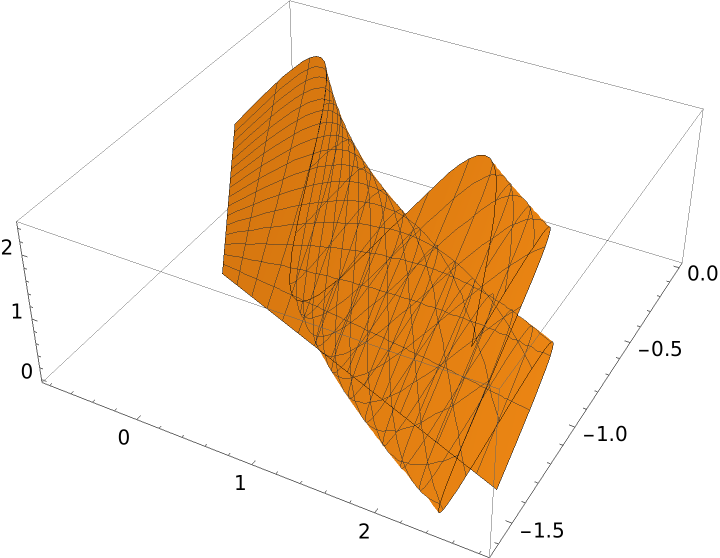 |
A curve not defined at some ranges:
| In[4]:= |
| Out[4]= | 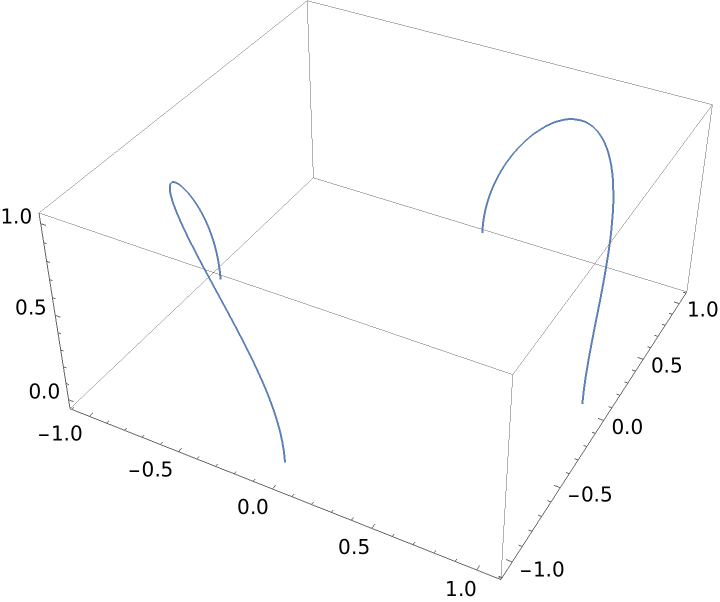 |
Show it with a projection:
| In[5]:= |
| Out[5]= | 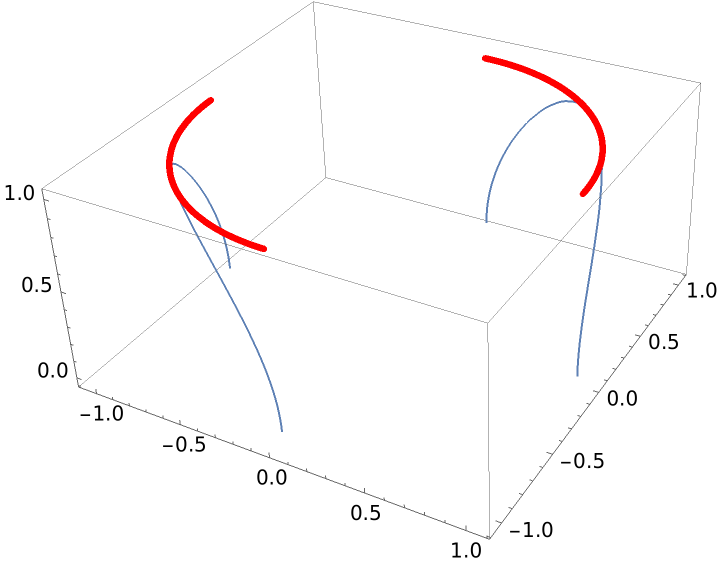 |
Define a graphic using a callout wrapper and show it along with its projection:
| In[6]:= | ![ParametricPlot3D[
Callout[{Sin[u], Sin[2 u], Cos[u]}, "original curve"], {u, 0, 2 Pi}];
Show[%, ResourceFunction["ProjectGraphics3D"][%, {0, 0, 1}, PlotStyle -> {Red, Thickness[.01]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/653f80f631e2fc3c.png) |
| Out[7]= | 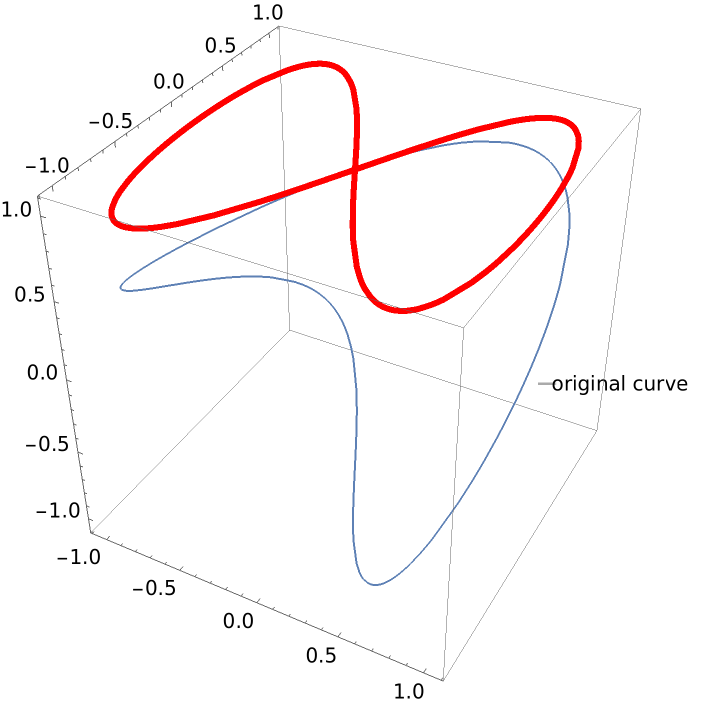 |
Show the correspondence between points in the helix and its projection:
| In[8]:= | ![helix = Entity["SpaceCurve", "Helix"]["ParametricEquations"][1, 1][
t]; points = Table[ResourceFunction["ProjectGraphics3D"][ Graphics3D[
Point[{Cos[t], Sin[t], t}]], {{1, 0, 0}, {0, 1, 1}}, {0, 0, 0}, {0, 0, 0}][[1, 1]], {t, 0, \[Pi], \[Pi]/12}]](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/63cc6e5eef36c5e0.png) |
| Out[9]= |  |
| In[10]:= | ![Show[gr, ResourceFunction["ProjectGraphics3D"][ gr, {{1, 0, 0}, {0, 1, 1}}, {0, 0, 0}, {0, 0, 0}, PlotStyle -> {Red, Thickness[.01]}], Graphics3D[{Arrow /@ N[Thread[{Table[helix, {t, 0, \[Pi], \[Pi]/12}], points}]], Opacity[.5], InfinitePlane[{{0, 0, 0}, {1, 0, 0}, {0, 1, 1}}]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/13ab87d49026dc6c.png) |
| Out[10]= | 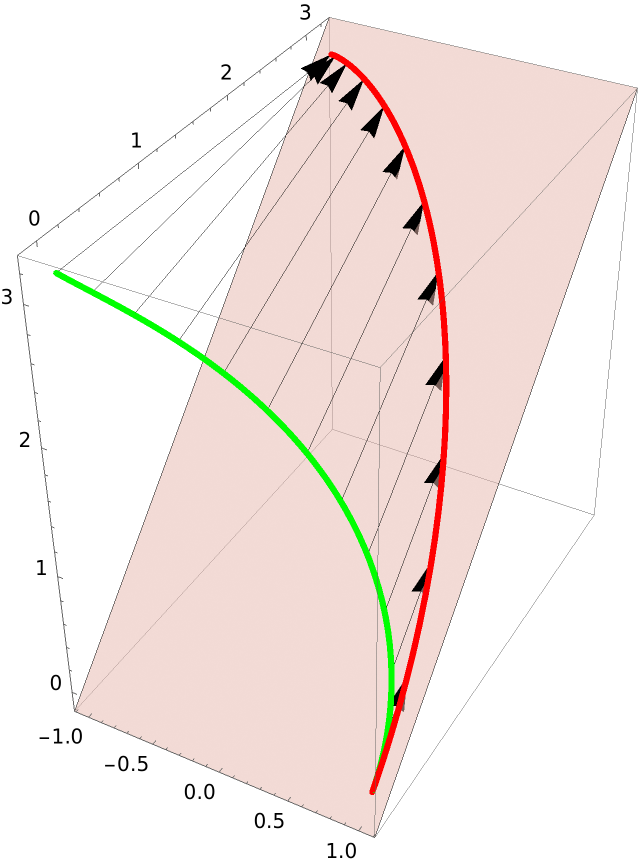 |
Project the curve in orthogonal planes:
| In[11]:= | ![Show[gr, ResourceFunction["ProjectGraphics3D"][ gr, # , {0, 0, 0}, PlotStyle -> {Red, Thickness[.01]}] & /@ {{{1, 0, 0}, {0, 1, 0}}, {{1, 0, 0}, {0, 0, 1}}, {{0, 1, 0}, {0, 0, 1}}}, Graphics3D[{Arrow[{{0, 0, 0}, #}] & /@ {{0, 1, 0}/2, {0, 0, 1}}, Opacity[.5], InfinitePlane[{{0, 0, 0}, {-1, 1, 0}, {1, 1, 0}}], InfinitePlane[{{0, 0, 0}, {-1, 0, 1}, {1, 0, 1}}], InfinitePlane[{{0, 0, 0}, {0, -1, 1}, {0, 1, 1}}]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/4b93b97a7fb80722.png) |
| Out[11]= | 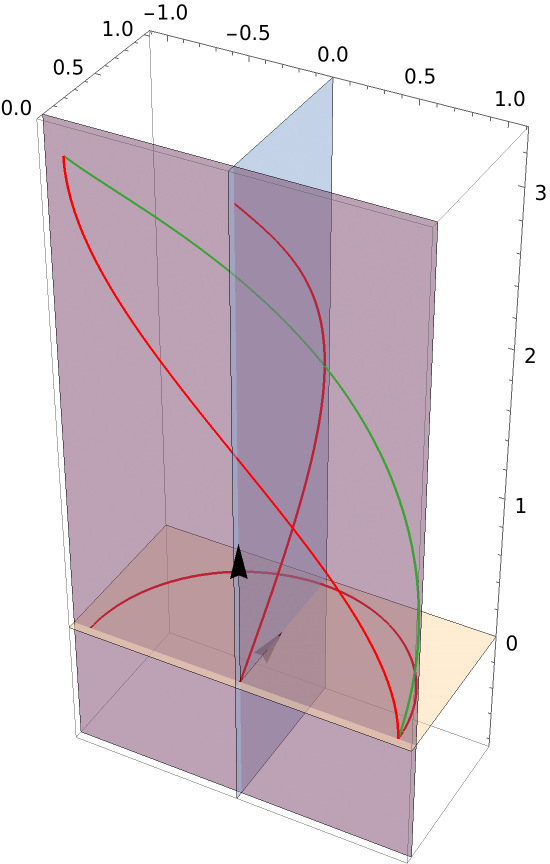 |
The rectifying plane:
| In[12]:= |
| Out[12]= |
The normal plane:
| In[13]:= |
| Out[13]= |
The osculating plane:
| In[14]:= |
| Out[14]= |
Show the projections of the curve in the normal and rectifying planes (the vectors are the tangent, normal and binormal vectors):
| In[15]:= | ![Manipulate[
Show[gr, ResourceFunction["ProjectGraphics3D"][ gr, #, helix /. t -> tf, PlotStyle -> Red] & /@ {rp[[2]], np[[2]], op[[2]]} /. t -> tf, Graphics3D[{{Arrowheads[.05], Blue, Arrow[{helix, helix + rp[[2, 1]]}], Arrow[{helix, helix + rp[[2, 2]]}],
Arrow[{helix, helix + np[[2, 1]]}]}, {Opacity[.5], rp, np, op}} /. t -> tf], PlotRange -> All], {{tf, 1}, 0, \[Pi]}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/5e374175806cd319.png) |
| Out[15]= | 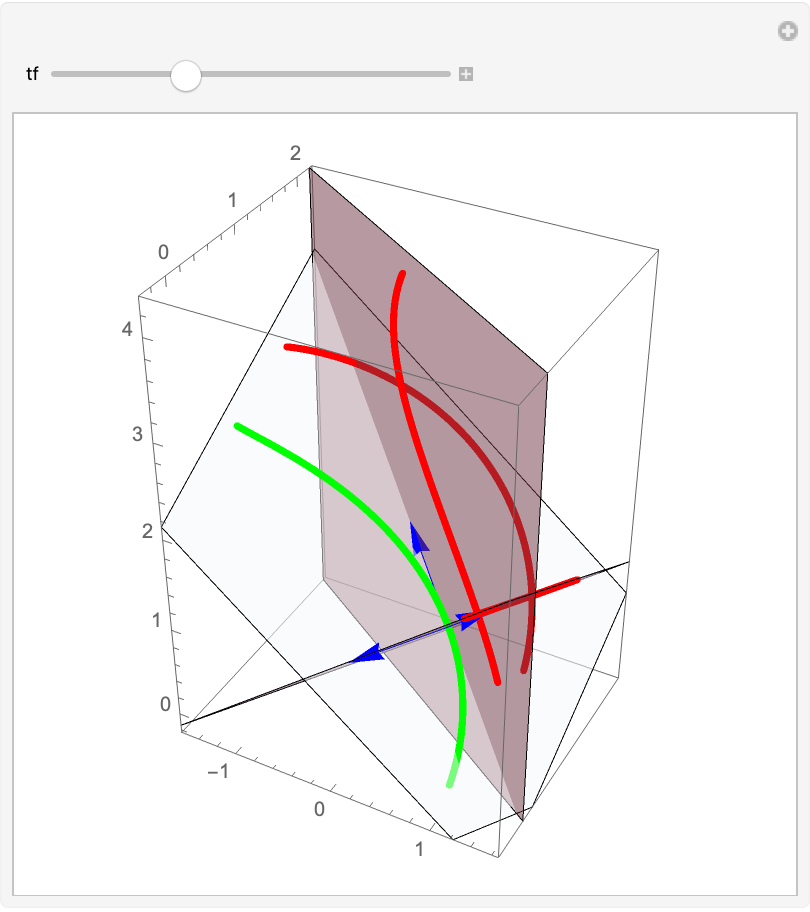 |
ProjectGraphics3D supports the same options as Graphics3D:
| In[16]:= |
| Out[16]= | 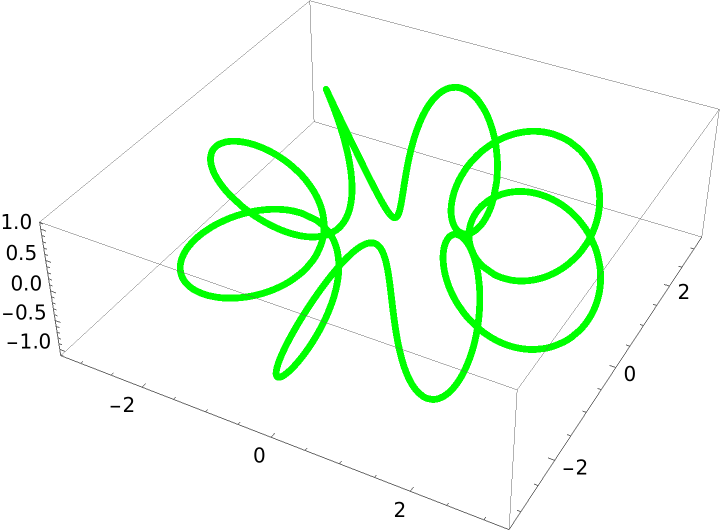 |
| In[17]:= | ![Show[ResourceFunction["ProjectGraphics3D"][%, {0, 1, 1}, PlotStyle -> {Red, Thickness[.01]}, FaceGrids -> All, FaceGridsStyle -> Directive[Orange, Dashed], PlotStyle -> {Red, Thickness[.01]}], %, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/02401e0fad00200e.png) |
| Out[17]= | 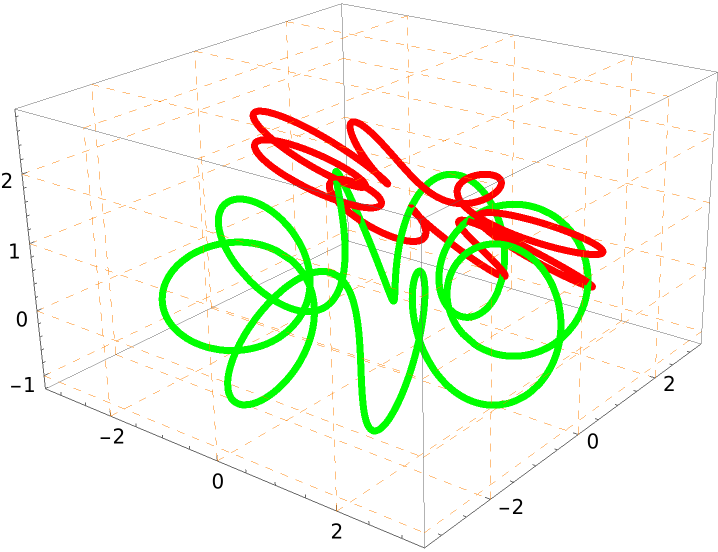 |
Get the equation for a helix:
| In[18]:= |
| Out[18]= |
Define a graphic output and compute its center:
| In[19]:= |
| Out[20]= |
Show the curve (green), its projection (red), and the plane of projection:
| In[21]:= | ![With[{p = {0, 0, 1}}, Show[gr, ResourceFunction["ProjectGraphics3D"][gr, p, PlotStyle -> {Red, Thickness[.01]}], Graphics3D[{Point[c], Arrow[{c, p}], Opacity[.5], InfinitePlane[{{1, 0, 0} + p, p, {0., -0.75221, 0.6589} + p}]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/56e64290097f0b20.png) |
| Out[21]= | 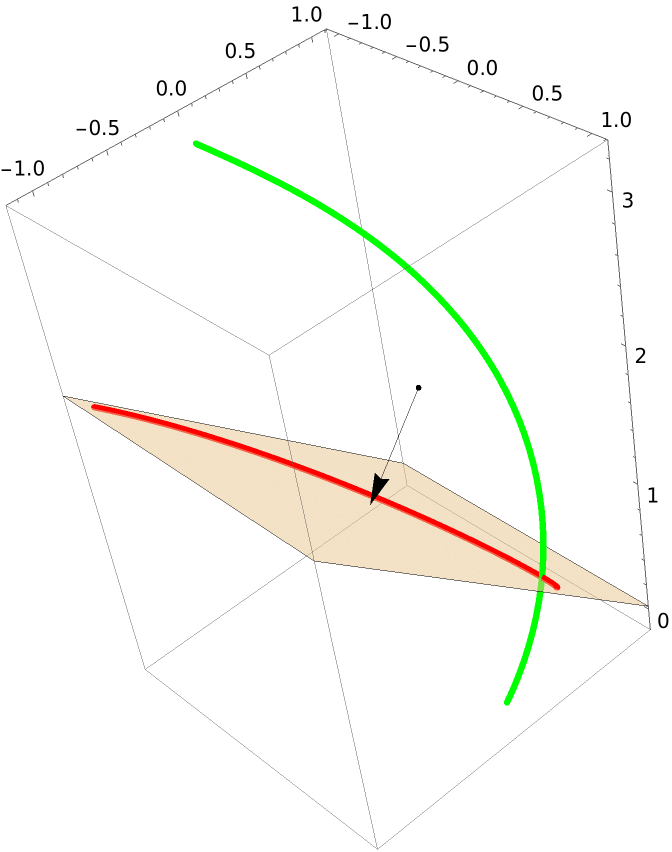 |
Hover the mouse over the curve:
| In[22]:= |
| In[23]:= |
| Out[23]= | 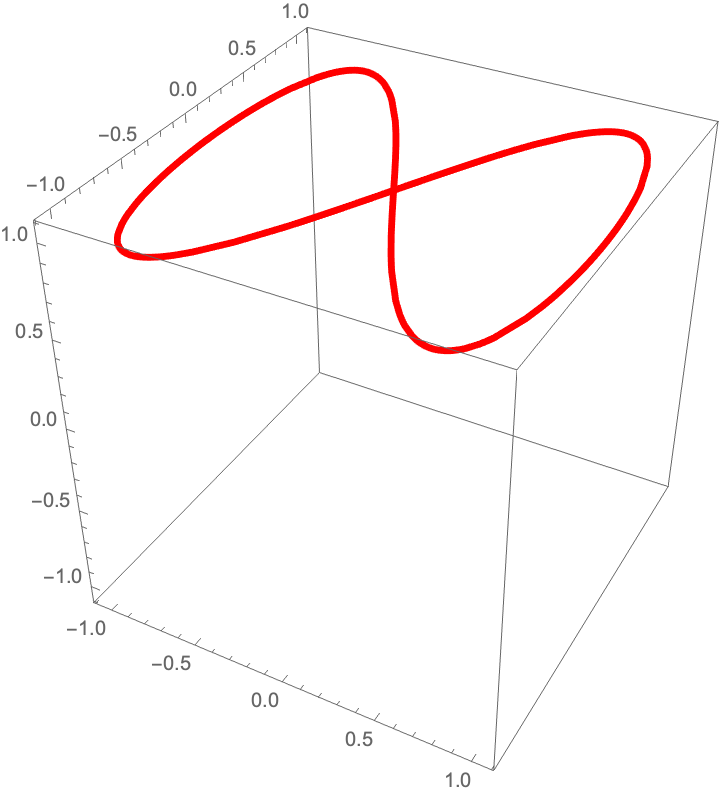 |
Move the spanning vectors and the location point:
| In[24]:= | ![helix = Entity["SpaceCurve", "Helix"]["ParametricEquations"][1, 1][
t];
gr = ParametricPlot3D[helix, {t, 0, \[Pi]}, PlotStyle -> {Green, Thickness[.01]}, PlotRange -> All];
c = Mean /@ AbsoluteOptions[gr, PlotRange][[1, 2]];](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/49bd976fdc470895.png) |
| In[25]:= | ![Manipulate[
Show[ResourceFunction["ProjectGraphics3D"][
gr, {{x, y, z}, {x1, y1, z1}}, {x2, y2, z2}, PlotStyle -> Red], gr,
Graphics3D[{Point[c], Arrow[{{0, 0, 0}, {x2, y2, z2}}], Arrow[{{x2, y2, z2}, # + {x2, y2, z2}}] & /@ {{x, y, z}, {x1, y1, z1}}, Opacity[.5],
InfinitePlane[{x2, y2, z2}, {{x, y, z}, {x1, y1, z1}}]}], PlotRange -> All],
{{x, 1}, -1, 1, ImageSize -> Tiny}, {{y, 0}, -1, 1, ImageSize -> Tiny}, {{z, 0}, -1, 1, ImageSize -> Tiny}, Delimiter,
{{x1, 0}, -1, 1, ImageSize -> Tiny}, {{y1, 1}, -1, 1, ImageSize -> Tiny}, {{z1, 0}, -1, 1, ImageSize -> Tiny}, Delimiter,
{{x2, 0}, -1, 1, ImageSize -> Tiny}, {{y2, 0}, -1, 1, ImageSize -> Tiny}, {{z2, 0}, -1, 1, ImageSize -> Tiny}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/559/5594f6ad-cf61-4462-b9e7-2bc5b390c970/5d80f53583c443c3.png) |
| Out[25]= | 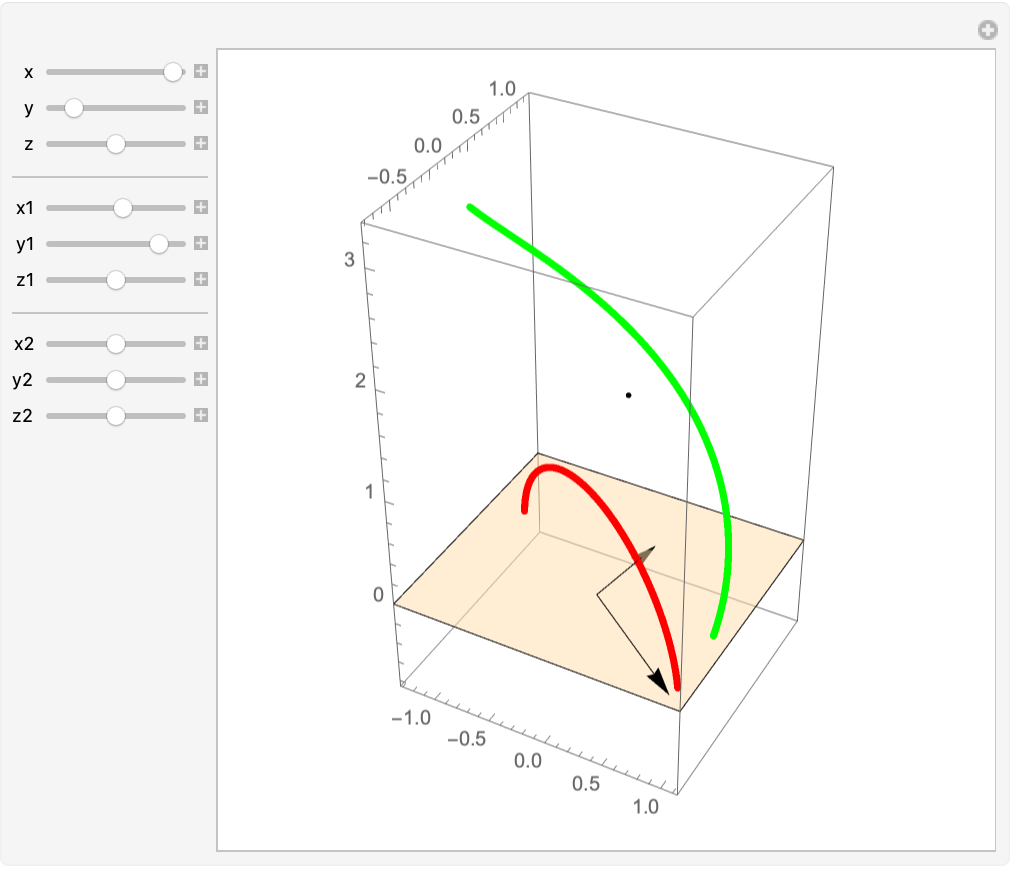 |
This work is licensed under a Creative Commons Attribution 4.0 International License