Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ProgressiveMaxPositions

Source Notebook

Find the positions of the largest elements so far in a list

Contributed by: Wolfram Staff (original work by Stephen Wolfram)

ResourceFunction["ProgressiveMaxPositions"][list]

gives the list of positions of the elements in list that are larger than any elements that appear before them.

Details

The elements corresponding to the positions returned by ResourceFunction["ProgressiveMaxPositions"] are sometimes referred to as high-water marks.

Examples

Basic Examples (1) 

Find the positions of elements that are larger than any of the ones that came before:

In[1]:=
ResourceFunction[ "ProgressiveMaxPositions"][{1, 1, 2, 5, 2, 2, 9, 1, 2, 11}]
Out[1]=

Applications (2) 

Find where progressively larger gaps between primes occur:

In[2]:=
ResourceFunction["ProgressiveMaxPositions"][ Differences[Array[Prime, 10^4]]]
Out[2]=

Compute the position of the head over 50 steps of Turing machine evolution:

In[3]:=
tm = TuringMachine[2506, {1, {{}, 0}}, 50]; hpos = tm[[All, 1, 3]]
Out[3]=

Find when the head is further to the right than ever before:

In[4]:=
hLeft = ResourceFunction["ProgressiveMaxPositions"][hpos]
Out[4]=

Find when the head is further to the left:

In[5]:=
hRight = ResourceFunction["ProgressiveMaxPositions"][-hpos]
Out[5]=

Show the compressed evolution of the Turing machine:

In[6]:=
With[{tc = tm[[Union[hLeft, hRight]]]}, ArrayPlot[ ArrayPad[tc[[All, 2]], {{0}, {1}}], {ColorRules -> {1 -> RGBColor[ 0.971, 0.6765, 0.09], _ -> White}, Epilog -> MapIndexed[ ResourceFunction["FiniteStateIndicatorIcon"][{#[[1, 2]] + 1/2, Length[tc] - First[#2] + 1/2}, {#[[1, 1]], 2}] &, tc]}]]
Out[6]=

Requirements

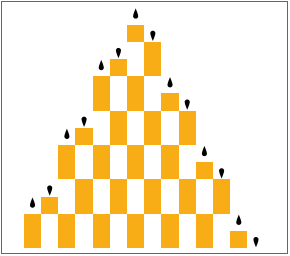
Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 14 September 2021
  • 1.0.0 – 10 December 2018

Related Resources

License Information