Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ProbNumObject

Source Notebook

PythonObject configuration for the Python package ProbNum

Contributed by: Igor Bakshee, with examples adapted from the ProbNum documentation.

ResourceFunction["ProbNumObject"][]

returns a configured PythonObject for the Python package ProbNum in a new Python session.

ResourceFunction["ProbNumObject"][session]

uses the specified running ExternalSessionObject session.

ResourceFunction["ProbNumObject"][…,"func"[args,opts]]

executes the function func with the specified arguments and options.

Details

The Python package Probabilistic Numerics (ProbNum) is a Python toolkit for solving numerical problems in linear algebra, optimization, quadrature and differential equations. The package solvers estimate both the solution of the numerical problem and its uncertainty, that is, the numerical error which arises from finite computational resources, discretization and stochastic input.
As of the ProbNum version v. 0.1.14, the available solvers include:
Linear solverssolve Ax=b for x
ODE solverssolve f(y(t),t) for y
Integral solverssolve for F
Lower level ProbNum objects include implementation of random variables and random processes, memory-efficient and lazy implementation of linear operators, and filtering and smoothing for probabilistic state-space models, mostly variants of Kalman filters.
ResourceFunction["ProbNumObject"] sets up a configuration of the resource function PythonObject that makes working with the Python package more convenient and returns the resulting Python object.
ResourceFunction["ProbNumObject"] makes the Python-side functions and objects accessible by new names that are closer to the usual Wolfram Language conventions.
For a Python object p, p["ToPythonName","wlname"] gives the name of the native Python function corresponding to the Wolfram Language name wlname and p["FromPythonName","pname"] gives the respective Wolfram Language name for the Python-side name pname. In the object p, both wlname and pname can be used interchangeably.
p["RenamingRules"] gives a list of all renaming rules in the form {"wlname1"→"pname1",…}.
p["FullInformation","Functions"] gives a list of the available functions and p["Information","func"] gives the signature of the specified function.
p["WebInformation"] gives a link to the ProbNum documentation that can be opened with SystemOpen.
Typically, the Wolfram Language signature of a ProbNum function closely resembles the Python-side signature in which Python-side objects are represented in the form of ResourceFunction["PythonObject"] with possible extensions suitable for the Wolfram Language.
In p["TimeSeriesRegressionProblem"[{t1,t2,…},obs,mods]], observations can be supplied as a Python object obs, defined on the time grid ti while possible values of measurement models mods include:
pthe same Python object p for all ti
{p1,p2,…}respective pi for ti
plista Python object representing a Python-side list of models
Additional utility functions are available in the form ResourceFunction["ProbNumObject"]["func"[args,opts]] or ResourceFunction["ProbNumObject"][session,"func"[…]], where session is a running ExternalSessionObject. The utility functions include:
"RNG"access the random number generator
“MeanPlots"plot mean solution values
"SamplePlots"plot ODE solution samples
"UncertaintyBandPlots"plot uncertainty bands
ResourceFunction["ProbNumObject"][session,"RNG"[seed]] seeds the default numpy random number generator in the running session, for reproducibility. ResourceFunction["ProbNumObject"][p,"RNG"[seed]] is the same as ResourceFunction["ProbNumObject"][p["Session"],"RNG"[seed]].
For a Python object solution representing an ODE solution, "MeanPlots"[solution,opts] gives a list of plots of mean values of the solution for each state variable. Accepts the options of ListLinePlot.
"SamplePlots"[rng,solution,nsampl,opts] gives a list of plots of samples of an ODE solution for each state using the random number generator seed rrng. Accepts the options of ListLinePlot. "SamplePlots"[rng,solution,nsampl,ns,opts] plots the samples on a subsampled grid, taking every ns-th point.
"UncertaintyBandPlots"[solution,opts] gives a list of plots of uncertainty bands of an ODE solution for each state. Accepts the options of ListLinePlot. "UncertaintyBandPlots"[solution,"meas",opts] plots the bands for the specified uncertainty measure "meas" with possible values "cov" representing the covariance or "std" representing the standard deviation. "UncertaintyBandPlots"[solution,"meas",band,opts] uses the specified numerical width of the band.
For sparse matrices, ResourceFunction["ProbNumObject"] automatically sets up Python object configuration using the resource function SciPyObject.

Examples

Basic Examples (3) 

Solve a linear matrix equation:

In[1]:=
a = {{7.5, 2., 1.}, {2., 2., 0.5}, {1., 0.5, 5.5}}; b = {1., 2., -3.};
In[2]:=
p = ResourceFunction["ProbNumObject"][]
Out[2]=
In[3]:=
solution = p["ProbabilisticLinearSolve"[a, b]] // Normal
Out[3]=

The multivariate Gaussian random variable corresponding to the solution:

In[4]:=
xRV = solution[[1]]
Out[4]=

The mean of the normal distribution equals the best guess for the solution of the linear system:

In[5]:=
xRV["mean"] // Normal // Normal
Out[5]=

The covariance matrix provides a measure of uncertainty:

In[6]:=
xRV["cov"]["ToDense"[]] // Normal // Normal
Out[6]=

In this case, the algorithm is very certain about the solution as the covariance matrix is virtually zero:

In[7]:=
Chop[%]
Out[7]=

Clean up by closing the Python session:

In[8]:=
DeleteObject[p["Session"]]

Deploy a Python function describing an ODE vector field in a Python session:

In[9]:=
session = StartExternalSession["Python"]
Out[9]=
In[10]:=
f = ResourceFunction["ToPythonFunction"][session, Function[{t, x}, 4 x (2 - x)]]
Out[10]=

Create a ProbNum Python object:

In[11]:=
p = ResourceFunction["ProbNumObject"][session]
Out[11]=

Solve the logistic ODE corresponding the field f with time running from t0 to tmax given the initial value vector y0:

In[12]:=
t0 = 0; tmax = 2; y0 = {0.001};
In[13]:=
solution = p["ProbabilisticSolveIVP"[f, t0, tmax, y0]]
Out[13]=

Obtain numerical values:

In[14]:=
solution["states"]["mean"] // Normal // Normal // Short
Out[14]=

Plot the solution:

In[15]:=
ResourceFunction["ProbNumObject"]["MeanPlots"[solution]]
Out[15]=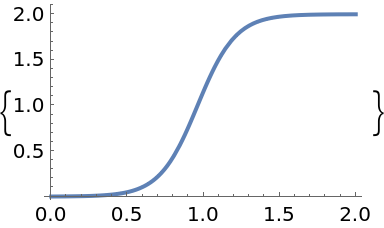

The uncertainty band around the solution is quite narrow indicating a high degree of certainty:

In[16]:=
ResourceFunction["ProbNumObject"][ "UncertaintyBandPlots"[solution, PlotStyle -> Automatic]]
Out[16]=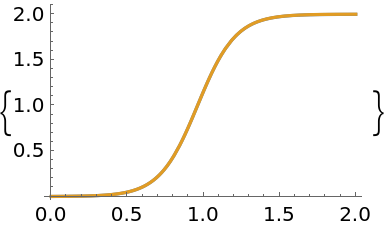
In[17]:=
DeleteObject[session]

Deploy a function in a Python session:

In[18]:=
session = StartExternalSession["Python"]
Out[18]=
In[19]:=
func = Function[x, 1/(x^3 + 1)]
Out[19]=
In[20]:=
f = ResourceFunction["ToPythonFunction"][session, func]
Out[20]=

Create a ProbNum Python object:

In[21]:=
p = ResourceFunction["ProbNumObject"][session]
Out[21]=
In[22]:=
inputDim = 1; domain = {0, 2};
In[23]:=
p["BayesianQuadrature"[f, inputDim, "Domain" -> domain]]
Out[23]=
In[24]:=
{res, bqinfo} = Normal[%]
Out[24]=

The mean value and standard deviation of the random variable represent the result of integration:

In[25]:=
res["mean.item()"]
Out[25]=
In[26]:=
res["std"]
Out[26]=

Additional information in bqinfo:

In[27]:=
bqinfo["Information"]
Out[27]=
In[28]:=
bqinfo["has_converged"]
Out[28]=

Compare with NIntegrate:

In[29]:=
NIntegrate[func[x], {x, 0, 2}]
Out[29]=

Clean up:

In[30]:=
DeleteObject[session]

Scope (23) 

Linear Algebra (11) 

Generate a random symmetric positive definite matrix with a given spectrum, seeding the random number generator for reproducibility:

In[31]:=
p = ResourceFunction["ProbNumObject"][]
Out[31]=
In[32]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[123]]
Out[32]=
In[33]:=
n = 25;
In[34]:=
spectrum = 10 Subdivide[0.5, 1, n - 1]^4
Out[34]=
In[35]:=
a = p["RandomSPDMatrix"[rng, n, "Spectrum" -> spectrum]]
Out[35]=

Define a random n⨯1 matrix:

In[36]:=
b = RandomReal[1, {n, 1}];

Visualize the linear system formed by the matrices:

In[37]:=
GraphicsRow[MatrixPlot /@ {Normal[a], b}]
Out[37]=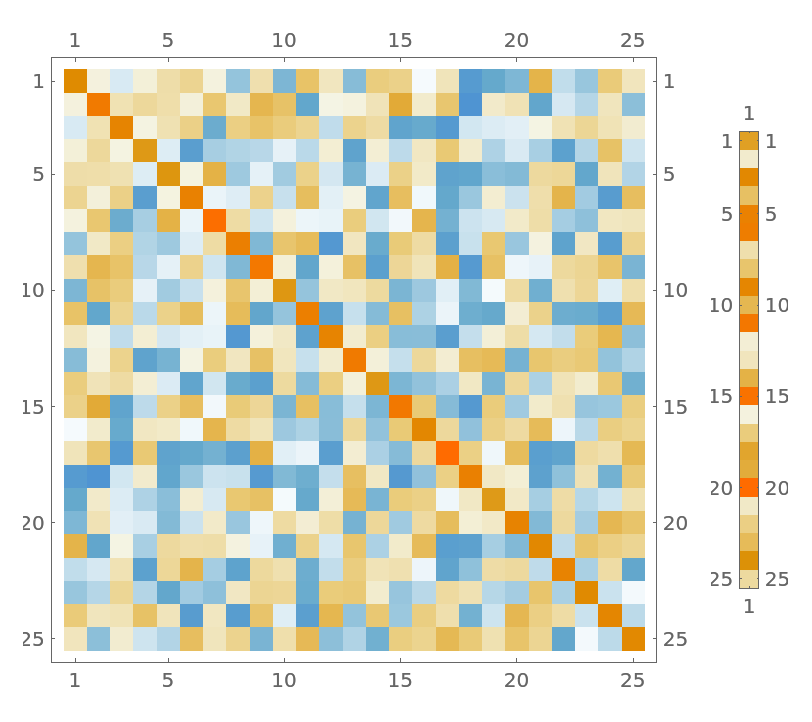

Solve the linear system a.x==b in a Bayesian framework using 10 iterations:

In[38]:=
{x, ah, ai, xinfo} = p["ProbabilisticLinearSolve"[a, b, MaxIterations -> 10]] // Normal
Out[38]=

The mean of the random variable x is the “best guess” for the solution:

In[39]:=
x["Mean"] // Normal
Out[39]=

Plot mean values of elements of the solution along with 68% credible intervals which capture per element distributions of x:

In[40]:=
ListPlot[ MapThread[ Around, {x["mean"] // Normal // Normal, x["std"] // Normal // Normal}], IntervalMarkers -> "Bars", PlotRange -> All]
Out[40]=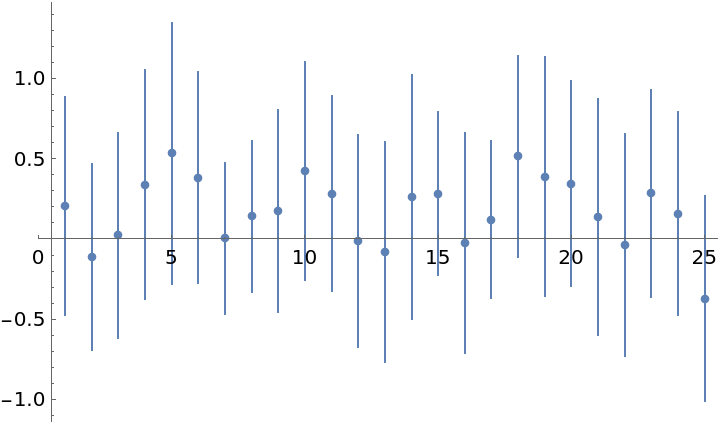

Samples from the normal distribution give possible solution vectors x1, x2, … which take into account cross correlations between the entries:

In[41]:=
Show[%, ListPlot[x["Sample"[rng, "Size" -> 10]] // Normal // Normal]]
Out[41]=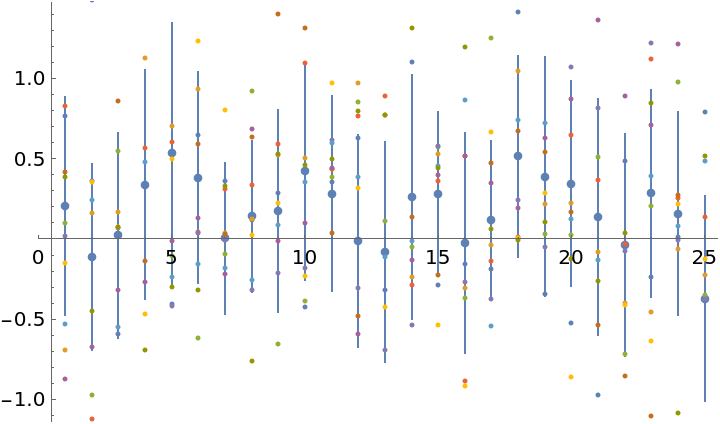

A more accurate solution can be obtained with more iterations or, for this system, with LinearSolve:

In[42]:=
xTrue = LinearSolve[Normal@Normal[a], Normal@Normal@b];

Even after 10 iterations, the ProbNum "best guess" solution is very close to the "true" solution:

In[43]:=
Show[%%, Prolog -> First@ListPlot[xTrue // Flatten, PlotStyle -> {{Red, PointSize[0.03]}}]]
Out[43]=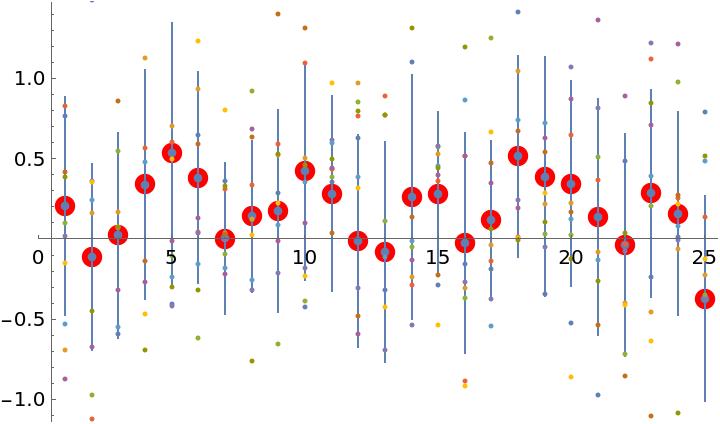

Maximal absolute and relative errors of the mean estimate:

In[44]:=
Max /@ {Abs[# - #2], Abs[# - #2]/Abs[# + #2]} & @@ {Normal[ Normal[x["Mean"]]], xTrue}
Out[44]=

The inverse of the matrix a looks close to its estimate ai. The latter maybe useful when obtaining the inverse directly is infeasible:

In[45]:=
GraphicsRow[ MatrixPlot /@ {ai["mean"]["ToDense"[]] // Normal, Inverse[a // Normal // Normal]}]
Out[45]=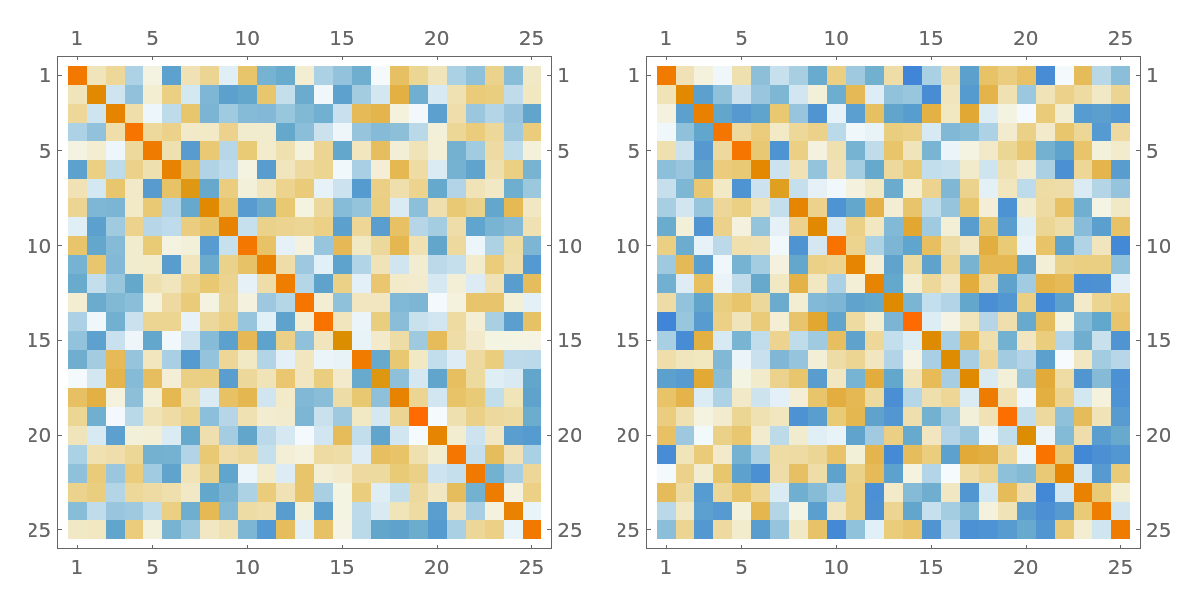
In[46]:=
DeleteObject[p["Session"]]

Ordinary Differential Equations (4) 

Filtering-based probabilistic ODE solver (7) 

Open a Python session:

In[47]:=
session = StartExternalSession["Python"]
Out[47]=
In[48]:=
p = ResourceFunction["ProbNumObject"][session]
Out[48]=

Define a vector field:

In[49]:=
f = ResourceFunction["ToPythonFunction"][session, Function[{t, x}, 4 x (2 - x)]]
Out[49]=

Solve an initial value problem (IVP) with a filtering-based probabilistic ODE solver using fixed steps:

In[50]:=
t0 = 0; tmax = 2; y0 = {0.001};
In[51]:=
solution = p["ProbabilisticSolveIVP"[f, t0, tmax, y0, "Step" -> 0.1, "Adaptive" -> False]]
Out[51]=

The mean of the discrete-time solution:

In[52]:=
solution["states"]["mean"] // Normal
Out[52]=

The time grid:

In[53]:=
solution["locations"] // Normal
Out[53]=

Plot the solution:

In[54]:=
ResourceFunction["ProbNumObject"]["MeanPlots"[solution]]
Out[54]=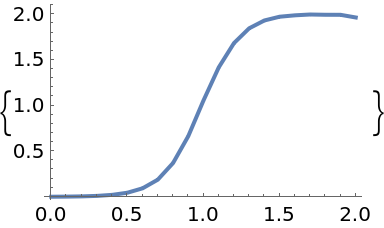

Construct and plot an interpolation corresponding to the continuous-time solution:

In[55]:=
Interpolation[ Transpose[{solution["locations"] // Normal // Normal, solution["states"]["mean"] // Normal // Normal}]]
Out[55]=
In[56]:=
Plot[%[x], {x, 0, 1.7}]
Out[56]=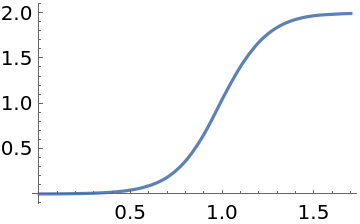
In[57]:=
DeleteObject[session]

Solve the same problem using the first-order extended Kalman filtering/smoothing:

In[58]:=
session = StartExternalSession["Python"];
In[59]:=
p = ResourceFunction["ProbNumObject"][session];

Vector field:

In[60]:=
f = ResourceFunction["ToPythonFunction"][session, Function[{t, x}, 4 x (2 - x)]]
Out[60]=

The Jacobian of the ODE vector field:

In[61]:=
df = ResourceFunction["ToPythonFunction"][session, Function[{t, x}, {4. - 8*x}], Method -> "np"]
Out[61]=

Solve the initial value problem:

In[62]:=
t0 = 0; tmax = 2; y0 = {0.001};
In[63]:=
solution = p["ProbabilisticSolveIVP"[f, t0, tmax, y0, "Df" -> df, Method -> "EK1", "AlgorithmOrder" -> 2, "Step" -> 0.1, "Adaptive" -> False]]
Out[63]=

Plot the solution:

In[64]:=
ResourceFunction["ProbNumObject"]["MeanPlots"[solution]]
Out[64]=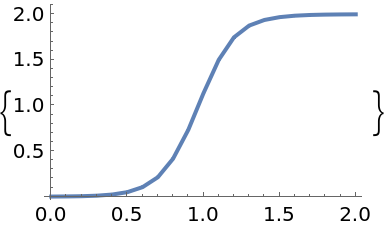

Clean up:

In[65]:=
DeleteObject[session]

Define the ODE for the Lotka-Volterra prey-predators problem:

In[66]:=
session = StartExternalSession["Python"];
In[67]:=
p = ResourceFunction["ProbNumObject"][session];
In[68]:=
f = ResourceFunction["ToPythonFunction"][session, Function[{t, y}, {0.5` y[[1]] - 0.05` y[[1]] y[[2]], -0.5` y[[2]] + 0.05` y[[1]] y[[2]]}], Method -> "np"]
Out[68]=
In[69]:=
df = ResourceFunction["ToPythonFunction"][session, Function[{t, y}, {{0.5` - 0.05` y[[2]], -0.05` y[[1]]}, {0.05` y[[2]], -0.5` + 0.05` y[[1]]}}], Method -> "np"]
Out[69]=

Solve with adaptive steps:

In[70]:=
t0 = 0; tmax = 20; y0 = {20, 20};
In[71]:=
solution = p["ProbabilisticSolveIVP"[f, t0, tmax, y0, "Df" -> df, Method -> "EK1", "AlgorithmOrder" -> 4]]
Out[71]=

Combine plots and notice smaller steps near solution peaks:

In[72]:=
plot[solution_] := Show[MapThread[ Legended[Show[# /. _RGBColor -> #2, Frame -> True], LineLegend[{#2}, {#3}]] &, {ResourceFunction["ProbNumObject"][ "MeanPlots"[solution, PlotLabel -> None]], {Darker[Green], Orange}, {"Prey", "Predators"}}], GridLines -> {solution["locations"] // Normal // Normal, Automatic}]
In[73]:=
plot[solution]
Out[73]=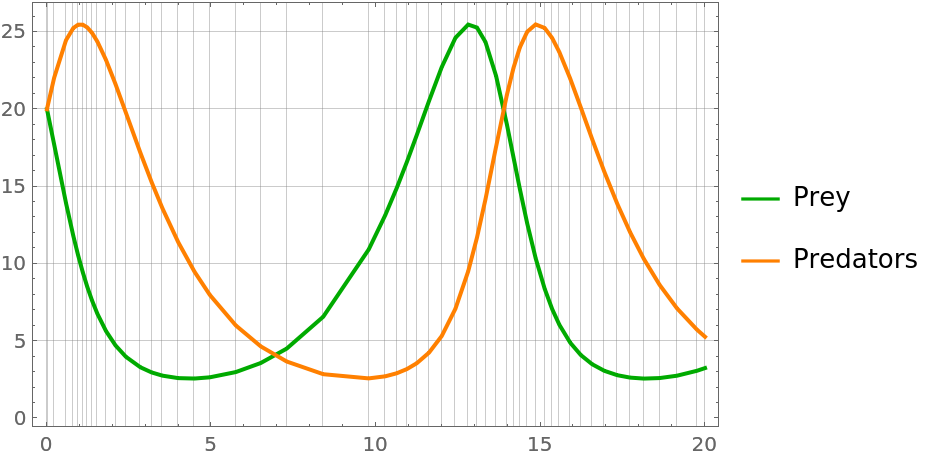

The higher-order filters takes fewer steps than the lower-order ones:

In[74]:=
GraphicsGrid@ Table[Show[ plot[p["ProbabilisticSolveIVP"[f, t0, tmax, y0, "Df" -> df, Method -> filter, "AlgorithmOrder" -> order]]] //. Legended[pl_, _] :> pl, PlotLabel -> StringTemplate["Order `order` with `filter`"][<|"order" -> order, "filter" -> filter|>]], {order, {2, 3}}, {filter, {"EK0", "EK1"}}]
Out[74]=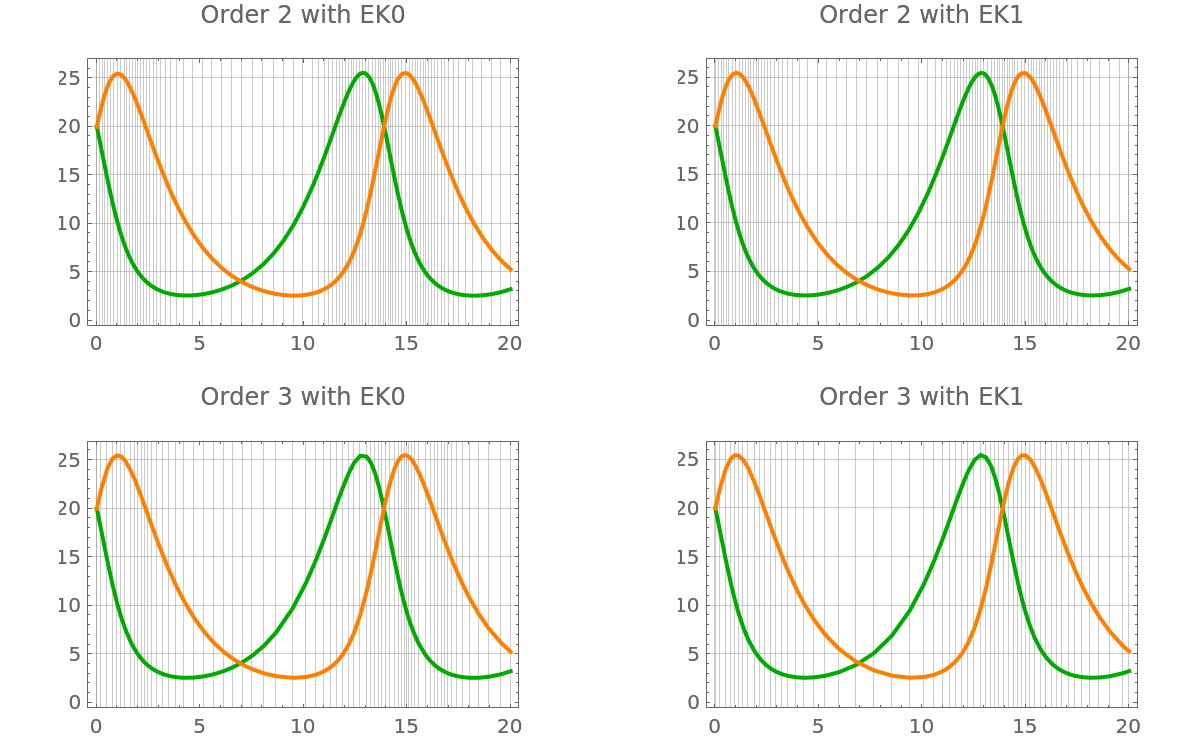
In[75]:=
DeleteObject[session]

To investigate uncertainties of the ODE solution, consider the same prey-predators problem:

In[76]:=
session = StartExternalSession["Python"];
In[77]:=
p = ResourceFunction["ProbNumObject"][session];
In[78]:=
f = ResourceFunction["ToPythonFunction"][session, Function[{t, y}, {0.5` y[[1]] - 0.05` y[[1]] y[[2]], -0.5` y[[2]] + 0.05` y[[1]] y[[2]]}], Method -> "np"];
In[79]:=
df = ResourceFunction["ToPythonFunction"][session, Function[{t, y}, {{0.5` - 0.05` y[[2]], -0.05` y[[1]]}, {0.05` y[[2]], -0.5` + 0.05` y[[1]]}}], Method -> "np"];

Obtain a low-resolution solution so that uncertainties are better visible:

In[80]:=
t0 = 0; tmax = 40; y0 = {20, 20};
In[81]:=
solution = p["ProbabilisticSolveIVP"[f, t0, tmax, y0, "Df" -> df, "AlgorithmOrder" -> 1, "Step" -> .5, "Adaptive" -> False, "diffusion_model" -> "dynamic"]]
Out[81]=

Prepare plots of uncertainty bands and a few samples from the solution:

In[82]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[1]]
Out[82]=
In[83]:=
ResourceFunction["ProbNumObject"]["UncertaintyBandPlots"[solution]];
In[84]:=
ResourceFunction["ProbNumObject"]["SamplePlots"[rng, solution, 5]];

Display the plots and notice that uncertainties are higher in valleys than in peaks; they also increase over time:

In[85]:=
MapThread[Show, {%%, %}]
Out[85]=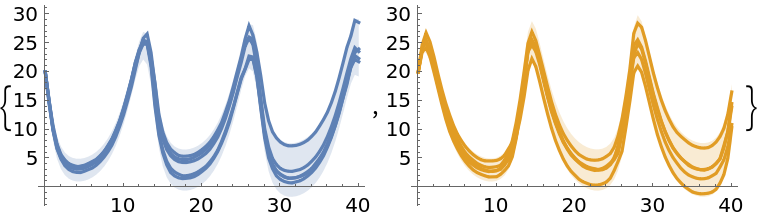
In[86]:=
DeleteObject[session]
Perturbation-based probabilistic ODE solver (5) 

Solve an initial value problem with a perturbation-based probabilistic ODE solver:

In[87]:=
session = StartExternalSession["Python"];
In[88]:=
f = ResourceFunction["ToPythonFunction"][session, Function[{t, x}, 4 x (1 - x)]]
Out[88]=
In[89]:=
p = ResourceFunction["ProbNumObject"][session]
Out[89]=
In[90]:=
t0 = 0; tmax = 1.5; y0 = {0.15};
In[91]:=
rng = ResourceFunction["ProbNumObject"][session, "RNG"[2]]
Out[91]=
In[92]:=
solution = p["PerturbationSolveIVP"[f, t0, tmax, y0, rng, "Step" -> 0.25, Method -> "RK23", "Adaptive" -> False]]
Out[92]=

Plot the solution:

In[93]:=
ResourceFunction["ProbNumObject"]["MeanPlots"[solution]]
Out[93]=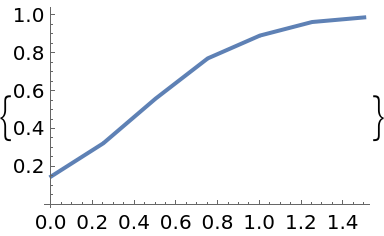

Each solution is the result of a randomly-perturbed call of an underlying Runge-Kutta solver. Therefore, the output is different for successive calls:

In[94]:=
Show[Table[ ResourceFunction["ProbNumObject"][ "MeanPlots"[ p["PerturbationSolveIVP"[f, t0, tmax, y0, rng, "Step" -> 0.25, Method -> "RK23", "Adaptive" -> False]]]], {5}]]
Out[94]=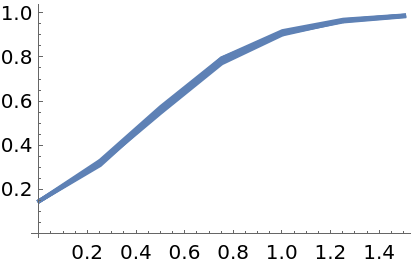

Solve the same equation, with an adaptive RK45 solver and uniformly perturbed steps:

In[95]:=
solution = p["PerturbationSolveIVP"[f, t0, tmax, y0, rng, "Perturbation" -> "step-uniform", "Atol" -> 10^-5, "Rtol" -> 10^-6, Method -> "RK45", "Adaptive" -> True]]
Out[95]=
In[96]:=
ResourceFunction["ProbNumObject"]["MeanPlots"[solution]]
Out[96]=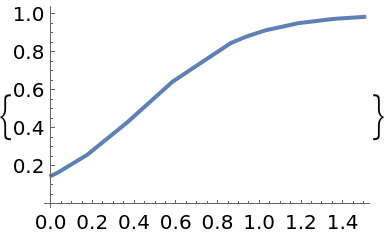

Clean up:

In[97]:=
DeleteObject[session]

Numerical Integration (2) 

Define a function and deploy it in a Python session:

In[98]:=
func = Function[x, Exp[Exp[-x]]]
Out[98]=
In[99]:=
session = StartExternalSession["Python"]
Out[99]=
In[100]:=
f = ResourceFunction["ToPythonFunction"][session, func]
Out[100]=

Create a ProbNum object:

In[101]:=
p = ResourceFunction["ProbNumObject"][session]
Out[101]=

Use the Bayesian Monte Carlo method to construct a a random variable, specifying the belief about the true value of the integral:

In[102]:=
inputDim = 1; domain = {0, 5};
In[103]:=
p["BayesianQuadrature"[f, inputDim, "Domain" -> domain]]
Out[103]=

The random variable and information about the integration:

In[104]:=
{res, bqinfo} = Normal[%]
Out[104]=

The mean value and standard deviation of the random variable representing the result of integration:

In[105]:=
res["mean.item()"]
Out[105]=
In[106]:=
res["std"]
Out[106]=

Samples of the variable:

In[107]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[1]]
Out[107]=
In[108]:=
res["Sample"[rng, "size" -> 500]]
Out[108]=
In[109]:=
Histogram[% // Normal // Normal]
Out[109]=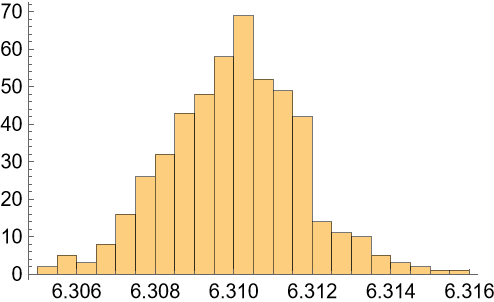

Compare with NIntegrate:

In[110]:=
NIntegrate[func[x], {x, 0, 5}]
Out[110]=

Clean up:

In[111]:=
DeleteObject[session]

Infer the value of an integral from a given set of nodes and function evaluations for the same problem:

In[112]:=
session = StartExternalSession["Python"]
Out[112]=
In[113]:=
p = ResourceFunction["ProbNumObject"][session]
Out[113]=
In[114]:=
nodes = List /@ Subdivide[0., 5., 100]; func = Function[x, Exp[Exp[-x]]]; vals = func[nodes];
In[115]:=
p["BayesianQuadratureFromData"[nodes, vals, "Domain" -> {0, 5}]]
Out[115]=
In[116]:=
{res, bqinfo} = Normal[%]
Out[116]=
In[117]:=
res["mean.item()"]
Out[117]=

Clean up:

In[118]:=
DeleteObject[p["Session"]]

Test Problems (6) 

Available test problems for probabilistic numerical methods:

In[119]:=
p = ResourceFunction["ProbNumObject"][]
Out[119]=
In[120]:=
zoo = p["problems"]["zoo"]
Out[120]=

Summary by module:

In[121]:=
Text[Grid[ Prepend[Table[{m, Grid[Module[{o = p[#1]}, {Hyperlink[#1, o["WebInformation"]], o["Information"]["Information"]}] & /@ zoo[m]["Information"]["Functions"], Alignment -> {{Right, Left}, Automatic}]}, {m, zoo["Information"][ "Modules"]}], (Style[#1, Bold] &) /@ {"Module", "Functions"}], Dividers -> Gray, Frame -> Gray, Spacings -> {Automatic, .8}, ItemStyle -> 14]]
Out[121]=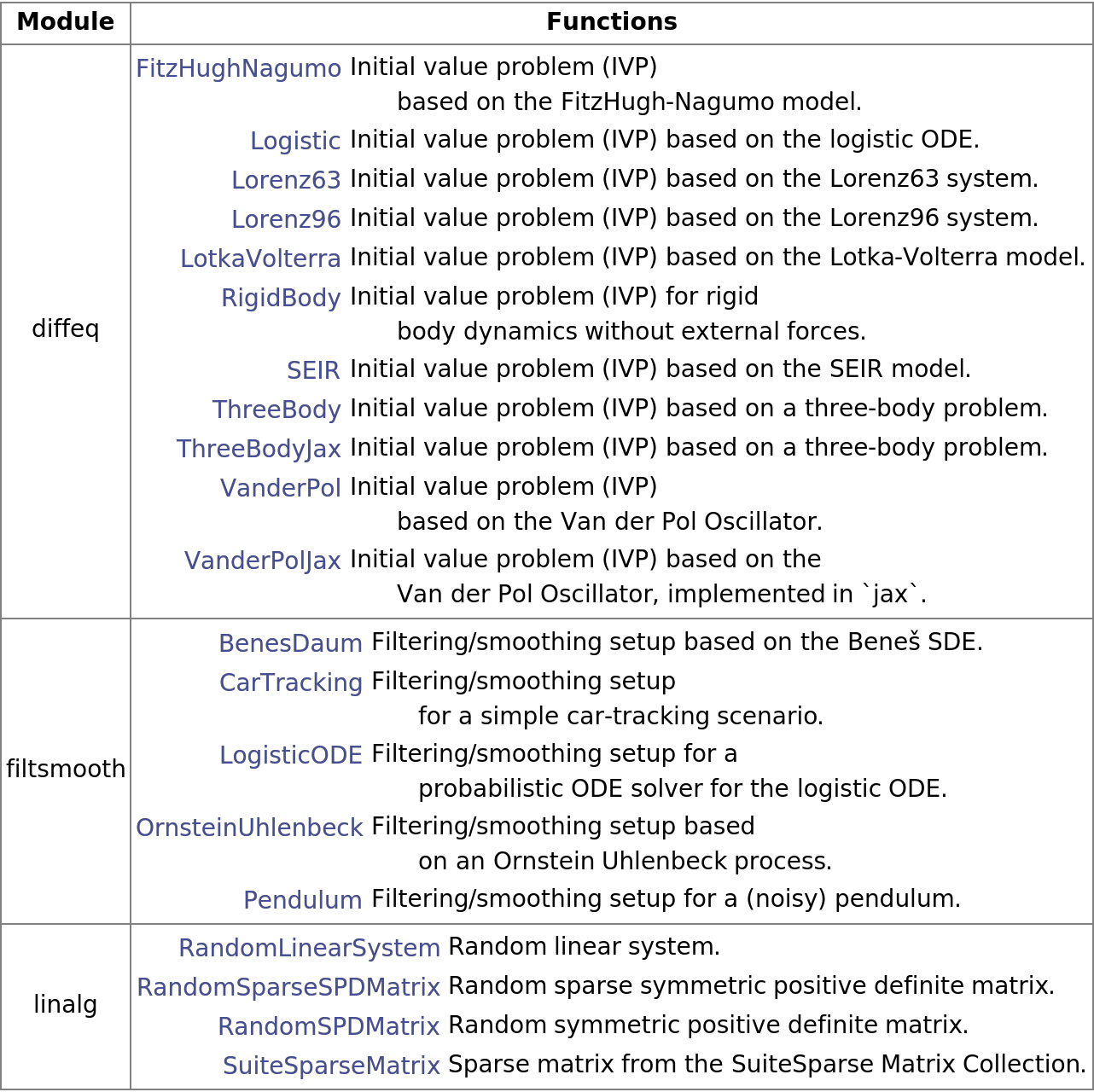
In[122]:=
DeleteObject[p["Session"]]
Initial Value Problems (5) 

Create a FitzHugh-Nagumo model with default parameters:

In[123]:=
p = ResourceFunction["ProbNumObject"][]
Out[123]=
In[124]:=
p["FitzHughNagumo"[]]
Out[124]=

Or supply optional parameters:

In[125]:=
ivp = p["FitzHughNagumo"["Tmax" -> 100, "Params" -> {0.2, 0.2, 0.6, 12.5}]]
Out[125]=

Find solution:

In[126]:=
solution = p["ProbabilisticSolveIVP"[ivp["f"], ivp["t0"], ivp["tmax"], ivp["y0"], "Atol" -> .2]]
Out[126]=

Samples from the solution:

In[127]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[1]]
Out[127]=
In[128]:=
samples = Show[ResourceFunction["ProbNumObject"][ "SamplePlots"[rng, solution, 10]]]
Out[128]=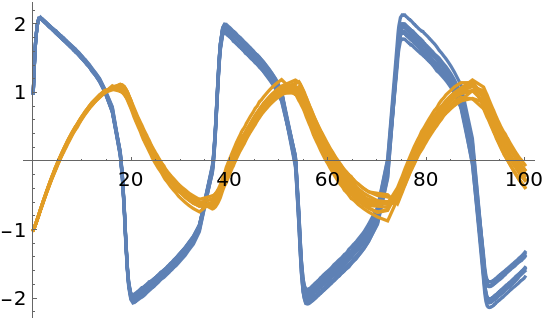

Plot together with mean values:

In[129]:=
Show[samples, ResourceFunction["ProbNumObject"]["MeanPlots"[solution]], Frame -> True, FrameLabel -> {"Time", "State variables"}, PlotLabel -> "FitzHugh-Nagumo model"]
Out[129]=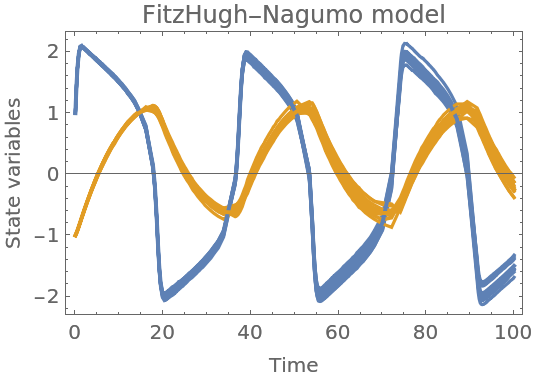
In[130]:=
DeleteObject[p["Session"]]

Create a model of the Lorenz63 system:

In[131]:=
p = ResourceFunction["ProbNumObject"][]
Out[131]=
In[132]:=
ivp = p["Lorenz63"[]]
Out[132]=

Find solution of the initial value problem:

In[133]:=
solution = p["ProbabilisticSolveIVP"[ivp["f"], ivp["t0"], ivp["tmax"], ivp["y0"], "Step" -> 1]]
Out[133]=

Plot the mean values:

In[134]:=
ResourceFunction["ProbNumObject"]["MeanPlots"[solution]]
Out[134]=

Numerical mean values:

In[135]:=
rvs = solution["states"]
Out[135]=
In[136]:=
means = rvs["mean"]
Out[136]=

Interpolate mean values:

In[137]:=
(locations = solution["locations"] // Normal // Normal) // Short
Out[137]=
In[138]:=
int = Interpolation[Transpose[{locations, #}]] & /@ Transpose[Normal[Normal[means]]]
Out[138]=
In[139]:=
ParametricPlot3D[#[t] & /@ int, {t, 0, 20}, PlotRange -> All]
Out[139]=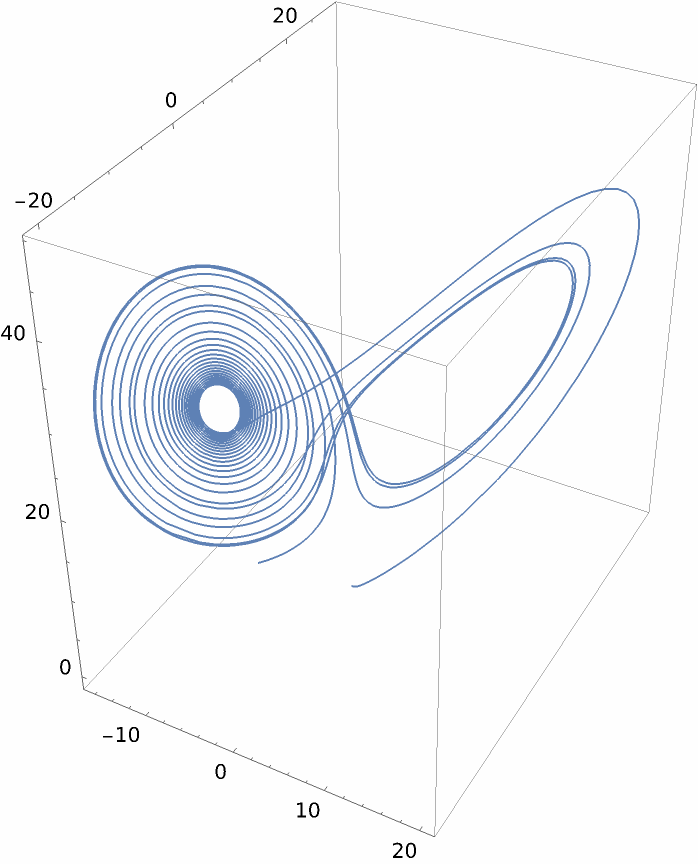
In[140]:=
DeleteObject[p["Session"]]
Random Symmetric Positive Definite Matrices (3) 

Create a random symmetric positive definite matrix:

In[141]:=
p = ResourceFunction["ProbNumObject"][]
Out[141]=
In[142]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[1]]
Out[142]=
In[143]:=
p["RandomSPDMatrix"[rng, 5]]
Out[143]=

Convert the object to a list of lists:

In[144]:=
Normal[%] // Normal
Out[144]=
Out[124]=
Out[145]=

Confirm that the matrix has the desired properties:

In[146]:=
SymmetricMatrixQ[%] && PositiveDefiniteMatrixQ[%]
Out[146]=
In[147]:=
DeleteObject[p["Session"]]

Create a random symmetric positive definite matrix with a predefined spectrum:

In[148]:=
p = ResourceFunction["ProbNumObject"][]
Out[148]=
In[149]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[1]]
Out[149]=
In[150]:=
n = 5;
In[151]:=
spectrum = 10 Subdivide[0.5, 1, n - 1]^4
Out[151]=
In[152]:=
p["RandomSPDMatrix"[rng, n, "Spectrum" -> spectrum]]
Out[152]=

Singular values of the matrix:

In[153]:=
SingularValueList[% // Normal // Normal]
Out[153]=
In[154]:=
% - Reverse[spectrum] // Chop
Out[154]=
In[155]:=
DeleteObject[p["Session"]]

Create a sparse random symmetric positive definite matrix:

In[156]:=
p = ResourceFunction["ProbNumObject"][]
Out[156]=
In[157]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[42]]
Out[157]=
In[158]:=
spd = p["RandomSparseSPDMatrix"[rng, 5, .1]]
Out[158]=

Convert the Python-side matrix to SparseArray:

In[159]:=
spdn = Normal[spd]
Out[159]=
In[160]:=
Normal[%] // TraditionalForm
Out[160]=

Confirm that the matrix has the desired properties:

In[161]:=
SymmetricMatrixQ[spdn] && PositiveDefiniteMatrixQ[spdn]
Out[161]=
In[162]:=
DeleteObject[p["Session"]]
SuiteSparse Matrices (4) 

Install the PythonPackage request if it's not installed on your system:

In[163]:=
session = StartExternalSession["Python"]
Out[163]=
In[164]:=
ResourceFunction["PythonPackageInstall"][session, "requests"]
Out[164]=

Obtain a sparse matrix from the SuiteSparse Matrix Collection:

In[165]:=
p = ResourceFunction["ProbNumObject"][session]
Out[165]=
In[166]:=
ssm = p["SuiteSparseMatrix"["ash85", "HB"]]
Out[166]=

Convert to SparseArray:

In[167]:=
sp = Normal[ssm]
Out[167]=
In[168]:=
MatrixPlot[sp]
Out[168]=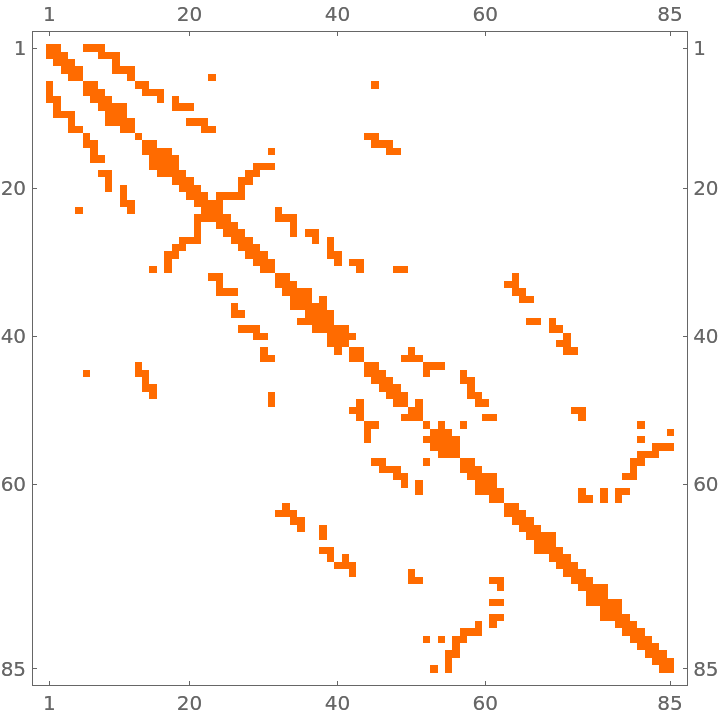

Compute the trace of the matrix on the Python side and in the Wolfram Language:

In[169]:=
ssm["Trace"[]]
Out[169]=
In[170]:=
Tr[sp]
Out[170]=
In[171]:=
DeleteObject[session]
Random Linear Systems (4) 

Define a unitary system matrix q:

In[172]:=
n = 5; a = RandomReal[1, {n, n}]; {q, r} = QRDecomposition[a]; q // TraditionalForm
Out[129]=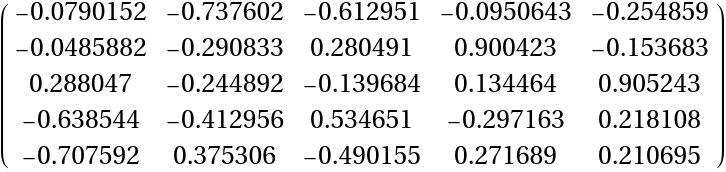
In[173]:=
UnitaryMatrixQ[q]
Out[173]=

Create a random linear state-space system with the given system matrix:

In[174]:=
p = ResourceFunction["ProbNumObject"][]
Out[174]=
In[175]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[42]]
Out[175]=
In[176]:=
ls = p["RandomLinearSystem"[rng, q]]
Out[176]=

The component matrices:

In[177]:=
{ls["A"], ls["B"]}
Out[177]=

Convert the Python object to the StateSpaceModel:

In[178]:=
Normal[ls]
Out[178]=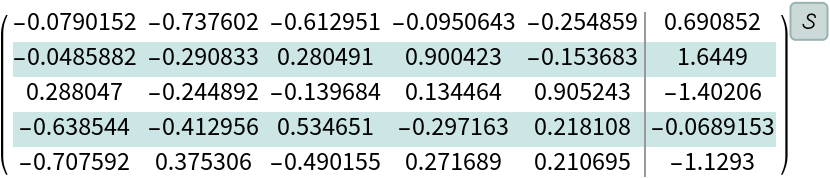
In[179]:=
DeleteObject[p["Session"]]

Create a linear system with a random symmetric positive-definite matrix:

In[180]:=
p = ResourceFunction["ProbNumObject"][]
Out[180]=
In[181]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[1]]
Out[181]=
In[182]:=
spd = p["RandomSPDMatrix"[rng, 5]]
Out[182]=
In[183]:=
ls = p["RandomLinearSystem"[rng, spd]]
Out[183]=

Convert to StateSpaceModel:

In[184]:=
Normal[ls]
Out[184]=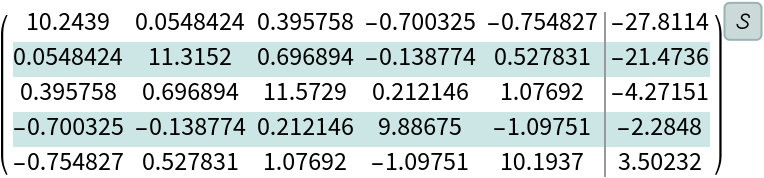
In[185]:=
DeleteObject[p["Session"]]

Use a sparse random symmetric positive-definite matrix as a system matrix:

In[186]:=
p = ResourceFunction["ProbNumObject"][]
Out[186]=
In[187]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[1]]
Out[187]=
In[188]:=
spd = p["RandomSparseSPDMatrix"[rng, 5, .1]]
Out[188]=
In[189]:=
ls = p["RandomLinearSystem"[rng, spd]]
Out[189]=

In the result, the given matrix a is sparse, and the matrix b is dense:

In[190]:=
Normal /@ {ls["A"], ls["B"]}
Out[190]=
In[191]:=
Normal[spd] == Normal@ls["A"]
Out[191]=
In[192]:=
DeleteObject[p["Session"]]

Applications (60) 

Linear Gaussian Filtering and Smoothing, Car Tracking  (17) 

Use Bayesian filtering and smoothing as a framework for efficient inference in state space models:

Model parameters:

In[193]:=
stateDimensions = 4; observationDimensions = 2;

Sampling period:

In[194]:=
deltaT = 0.2;

Linear transition operator:

In[195]:=
(dynamicsTransitionMatrix = IdentityMatrix[stateDimensions] + deltaT*DiagonalMatrix[{1, 1}, 2]) // MatrixForm
Out[195]=

Zero-valued force vector for affine transformations of the state:

In[196]:=
forceVector = ConstantArray[0., stateDimensions]
Out[196]=

Covariance matrix of the Gaussian process noise:

In[197]:=
(processNoiseMatrix = DiagonalMatrix[{1/3 deltaT^3, 1/3 deltaT^3, deltaT, deltaT}] + DiagonalMatrix[{deltaT^2/2, deltaT^2/2}, 2] + DiagonalMatrix[{deltaT^2/2, deltaT^2/2}, -2]) // MatrixForm
Out[197]=

Define a linear, time-invariant (LTI) discrete Gaussian state-space dynamics model:

In[198]:=
p = ResourceFunction["ProbNumObject"][]
Out[198]=
In[199]:=
noise = p[ "Normal"[ConstantArray[0., stateDimensions], processNoiseMatrix]]
Out[199]=
In[200]:=
dynamicsModel = p["LTIGaussian"["transition_matrix" -> dynamicsTransitionMatrix, "noise" -> noise]]
Out[200]=

A discrete LTI Gaussian measurement model:

In[201]:=
measurementMarginalVariance = 0.5;
In[202]:=
(measurementMatrix = IdentityMatrix[{observationDimensions, stateDimensions}]) // MatrixForm
Out[202]=
In[203]:=
(measurementNoiseMatrix = measurementMarginalVariance* IdentityMatrix[observationDimensions]) // MatrixForm
Out[203]=
In[204]:=
mnoise = p["Normal"[ConstantArray[0., observationDimensions], measurementNoiseMatrix]]
Out[204]=
In[205]:=
measurementModel = p["LTIGaussian"["TransitionMatrix" -> measurementMatrix, "Noise" -> mnoise]]
Out[205]=

An initial state random variable:

In[206]:=
mu0 = ConstantArray[0., stateDimensions]
Out[206]=
In[207]:=
sigma0 = 0.5*measurementMarginalVariance*IdentityMatrix[stateDimensions]
Out[207]=
In[208]:=
initialStateRv = p["Normal"[mu0, sigma0]]
Out[208]=

A memoryless prior process:

In[209]:=
priorProcess = p["MarkovProcess"[0., initialStateRv, dynamicsModel]]
Out[209]=

Generate data samples of latent states and noisy observations from the specified state space model:

In[210]:=
timeGrid = Range[0., 10., deltaT];
In[211]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[123]]
Out[211]=
In[212]:=
p["GenerateArtificialMeasurements"[rng, priorProcess, measurementModel, timeGrid]]
Out[212]=
In[213]:=
{latentStates, observations} = Normal[%]
Out[213]=
In[214]:=
regressionProblem = p["TimeSeriesRegressionProblem"[timeGrid, observations, measurementModel]]
Out[214]=

Create a Kalman filter:

In[215]:=
kalmanFilter = p["Kalman"[priorProcess]]
Out[215]=

Perform Kalman Filtering with a Rauch-Tung-Striebel smoothing:

In[216]:=
kalmanFilter["filtsmooth"[regressionProblem]]
Out[216]=
In[217]:=
{statePosterior, infoList} = Normal[%]
Out[217]=

To visualize the results, prepare plots of mean values from the state posterior object:

In[218]:=
means = ResourceFunction["ProbNumObject"][ "MeanPlots"[statePosterior, PlotRange -> All]];

Observation plots:

In[219]:=
obs = ListPlot[Transpose[{timeGrid, #}], PlotStyle -> {Red, Large}] & /@ Transpose[Normal@Normal[observations]];

Uncertainty bands:

In[220]:=
bands = ResourceFunction["ProbNumObject"][ "UncertaintyBandPlots"[statePosterior]];

Combine the plots:

In[221]:=
Grid@Partition[ Show[##2, PlotRange -> All, PlotLabel -> Subscript["x", #]] & @@@ Transpose[{Range[Length[means]], means, Join[obs, {{}, {}}], bands}], 2]
Out[221]=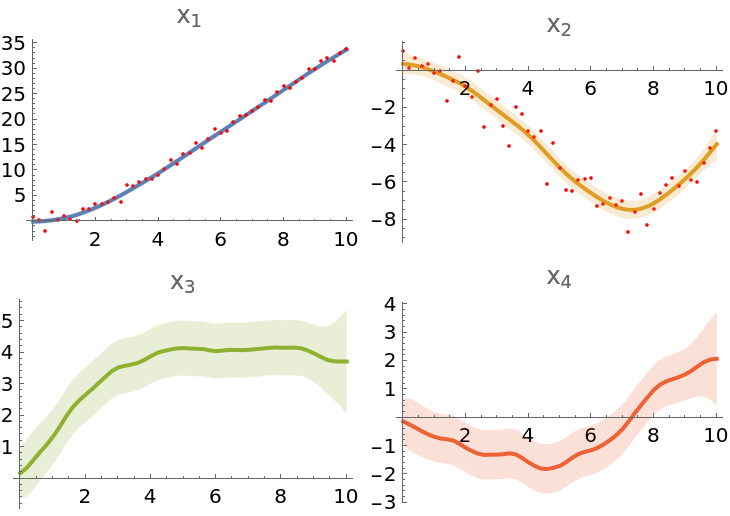
In[222]:=
DeleteObject[p["Session"]]

Nonlinear Gaussian Filtering and Smoothing, Pendulum (18) 

Use linearization techniques for Gaussian filtering and smoothing in more complex dynamical systems, such as a pendulum:

Acceleration due to gravity:

In[223]:=
g = 9.81;

Model parameters:

In[224]:=
stateDimensions = 2; observationDimensions = 1;

Sampling period:

In[225]:=
deltaT = 0.0075;

Define a dynamics transition function and its Jacobian, ignoring the time variable t for time-invariant models:

In[226]:=
session = StartExternalSession["Python"];
In[227]:=
p = ResourceFunction["ProbNumObject"][session]
Out[227]=
In[228]:=
dynamicsTransitionFunction = ResourceFunction["ToPythonFunction"][session, Function[{t, state}, {x1 + x2*deltaT, x2 - g*Sin[x1]*deltaT}] /. {x1 :> state[[1]], x2 :> state[[2]]}, Method -> "np"]
Out[228]=
In[229]:=
dynamicsTransitionJacobianFunction = ResourceFunction["ToPythonFunction"][session, Function[{t, state}, {{1, deltaT}, {-g * Cos[x1] * deltaT, 1.}}] /. {x1 :> state[[1]], x2 :> state[[2]]}, Method -> "np"]
Out[229]=

Diffusion matrix:

In[230]:=
dynamicsDiffusionMatrix = DiagonalMatrix[{deltaT^3/3, deltaT}] + DiagonalMatrix[{deltaT^2/2}, 1] + DiagonalMatrix[{deltaT^2/2}, -1]
Out[230]=
In[231]:=
noise = p[ "Normal"[ConstantArray[0., stateDimensions], dynamicsDiffusionMatrix]]
Out[231]=
In[232]:=
noiseFunction = ResourceFunction["ToPythonFunction"][session, Function[t, noise]]
Out[232]=

Create a discrete, non-linear Gaussian dynamics model:

In[233]:=
dynamicsModel = p["NonlinearGaussian"["InputDim" -> stateDimensions, "OutputDim" -> stateDimensions, "TransitionFunction" -> dynamicsTransitionFunction, "NoiseFunction" -> noiseFunction, "TransitionFunctionJacobian" -> dynamicsTransitionJacobianFunction]]
Out[233]=

Prepare functions that define nonlinear Gaussian measurements:

In[234]:=
measurementFunction = ResourceFunction["ToPythonFunction"][session, Function[{t, state}, {Sin[state[[1]]]}], Method -> "np"]
Out[234]=
In[235]:=
measurementJacobianFunction = ResourceFunction["ToPythonFunction"][session, Function[{t, state}, {{Cos[state[[1]]], 0.}}], Method -> "np"]
Out[235]=
In[236]:=
measurementVariance = 0.32^2
Out[236]=
In[237]:=
measurementCovarianceMatrix = measurementVariance*IdentityMatrix[observationDimensions]
Out[237]=
In[238]:=
measurementNoise = noise = p[ "Normal"[ConstantArray[0., observationDimensions], measurementCovarianceMatrix]]
Out[238]=
In[239]:=
measurementNoiseFunction = ResourceFunction["ToPythonFunction"][session, Function[t, measurementNoise]]
Out[239]=

Create discrete, non-linear Gaussian measurement model:

In[240]:=
measurementModel = p["NonlinearGaussian"["InputDim" -> stateDimensions, "OutputDim" -> observationDimensions, "TransitionFunction" -> measurementFunction, "NoiseFunction" -> measurementNoiseFunction, "TransitionFunctionJacobian" -> measurementJacobianFunction]]
Out[240]=

Initial state random variable:

In[241]:=
mu0 = ConstantArray[0., stateDimensions]
Out[241]=
In[242]:=
sigma0 = measurementVariance*IdentityMatrix[stateDimensions]
Out[242]=
In[243]:=
initialStateRv = p["Normal"[mu0, sigma0]]
Out[243]=

Linearize the model to create the Extended Kalman Filter (EKF):

In[244]:=
linearisedDynamicsModel = p["DiscreteEKFComponent"[dynamicsModel]]
Out[244]=
In[245]:=
priorProcess = p["MarkovProcess"[0., initialStateRv, linearisedDynamicsModel]]
Out[245]=
In[246]:=
kalmanFilter = p["Kalman"[priorProcess]]
Out[246]=

Generate data for the state-space model:

In[247]:=
timeGrid = Range[0., 5, deltaT];
In[248]:=
rng = ResourceFunction["ProbNumObject"][session, "RNG"[123]]
Out[248]=
In[249]:=
p["GenerateArtificialMeasurements"[rng, priorProcess, measurementModel, timeGrid]]
Out[249]=
In[250]:=
{latentStates, observations} = Normal[%]
Out[250]=
In[251]:=
regressionProblem = p["TimeSeriesRegressionProblem"[timeGrid, observations, p["DiscreteEKFComponent"[measurementModel]]]]
Out[251]=

Perform Kalman filtering with Rauch-Tung-Striebel smoothing:

In[252]:=
kalmanFilter["filtsmooth"[regressionProblem]]
Out[252]=
In[253]:=
{statePosterior, infoList} = Normal[%]
Out[253]=

Prepare mean value plots of the state posterior object:

In[254]:=
means = ResourceFunction["ProbNumObject"][ "MeanPlots"[statePosterior]];

Display a few samples from the state posterior on a subsampled grid, taking every fifth point for clarity:

In[255]:=
psamples = ResourceFunction["ProbNumObject"][ "SamplePlots"[rng, statePosterior, 4, 5]]
Out[255]=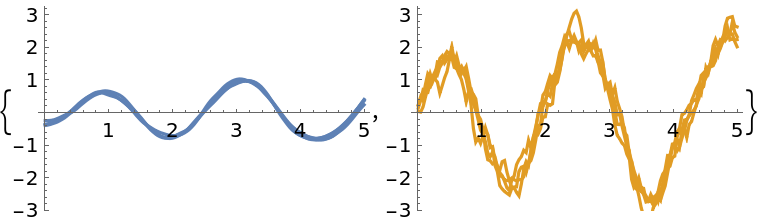

Prepare plots of uncertainty bands:

In[256]:=
bands = ResourceFunction["ProbNumObject"][ "UncertaintyBandPlots"[statePosterior]];

Observations:

In[257]:=
obs = ListPlot[Transpose[{timeGrid, #}], PlotStyle -> {Red, Large}] & /@ Transpose[Normal@Normal[observations]];

Combine the plots:

In[258]:=
GraphicsColumn[{Show[bands[[1]], psamples[[1]], means[[1]], obs, PlotRange -> All, PlotLabel -> Subscript[x, 1]], Show[bands[[2]], psamples[[2]], means[[2]], PlotLabel -> Subscript[x, 2]]}]
Out[258]=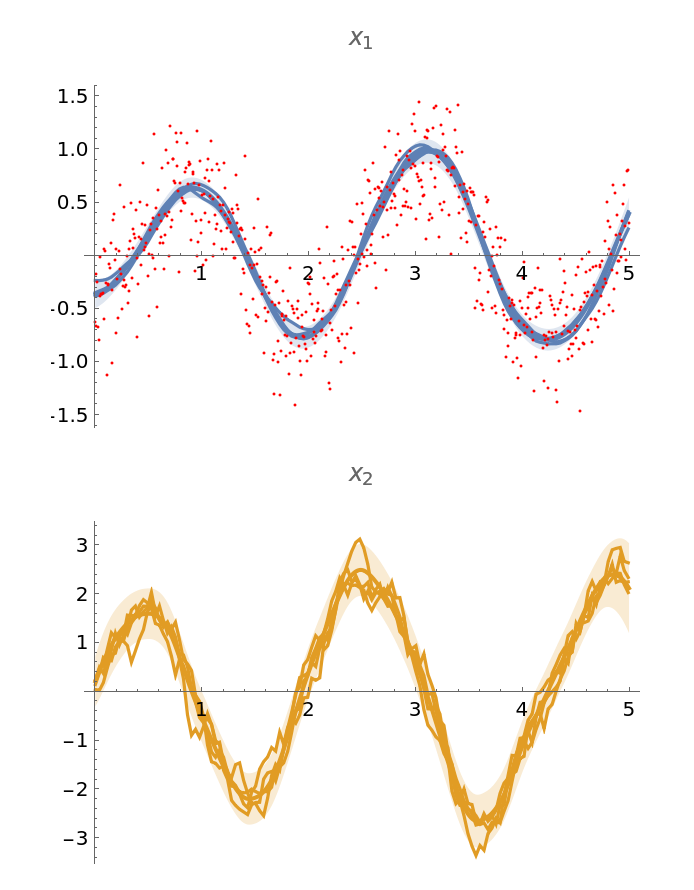
In[259]:=
DeleteObject[session]

Particle filtering (25) 

Use a set of particles (samples) to represent the posterior distribution of a stochastic process given noisy observations.

Pendulum (11) 

Create a pendulum model from scratch, as in the Nonlinear Gaussian Filtering and Smoothing example, or use a predefined test problem:

In[260]:=
p = ResourceFunction["ProbNumObject"][]
Out[260]=
In[261]:=
rng = ResourceFunction["ProbNumObject"][p, "RNG"[123]]
Out[261]=
In[262]:=
{regressionProblem, rpInfo} = Normal@p[ "Pendulum"[rng, "MeasurementVariance" -> 0.12^2, "Timespan" -> {0, 3.5}, "Step" -> 0.05]]
Out[262]=

Extract parameters needed to set up a particle filer, starting from the prior process:

In[263]:=
rpInfo // Normal
Out[263]=
In[264]:=
priorProcess = Normal["prior_process" /. %][[1]]
Out[264]=

Also get the dynamics model and the measurement model:

In[265]:=
dynamicsModel = priorProcess["transition"]
Out[265]=
In[266]:=
measurementModel = regressionProblem["measurement_models"]["__getitem__"[0]]
Out[266]=

Create a linearized the importance distribution from the extended Kalman filer:

In[267]:=
fromEKF = p["LinearizationImportanceDistribution"]["FromEKF"]
Out[267]=
In[268]:=
importanceDistribution = fromEKF[All][dynamicsModel]
Out[268]=

Define the number of particles:

In[269]:=
numParticles = 20;

Create a particle filter:

In[270]:=
pf = p["ParticleFilter"[ priorProcess, importanceDistribution, numParticles, rng]]
Out[270]=

Apply the filter and obtain the posterior distribution:

In[271]:=
pf["Filter"[regressionProblem]]
Out[271]=
In[272]:=
posterior = Normal[%] // First
Out[272]=

The states of posterior:

In[273]:=
states = posterior["States"]
Out[273]=

Plot the latent state together with the mode of the posterior distribution:

In[274]:=
latentState = Transpose[regressionProblem["solution"] // Normal // Normal][[1]];
In[275]:=
locations = regressionProblem["locations"] // Normal // Normal;
In[276]:=
lsplot = ListLinePlot[Transpose[{locations, latentState}], PlotStyle -> Thick];
In[277]:=
mode = Transpose[states["mode"] // Normal // Normal][[1]];
In[278]:=
Show[{lsplot}, ListPlot[Transpose[{locations, mode}], PlotStyle -> Red]]
Out[278]=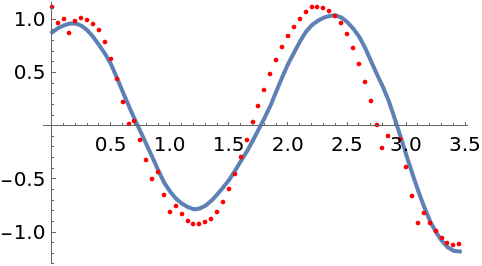

The true latent state is recovered fairly well. The root-mean-square error (RNSE) of the mode is also much smaller than the RMSE of the data:

In[279]:=
rmseMode = Norm[mode - latentState]
Out[279]=
In[280]:=
observations = regressionProblem["observations"] // Normal // Normal // Flatten;
In[281]:=
rmseData = Norm[Outer[# - #2 &, observations, latentState], "Frobenius"]
Out[281]=

Plot a few more particles, removing the unlikely ones by resampling the posterior. The distribution concentrates around the true state:

In[282]:=
resampledStates = states["resample"[rng]]
Out[282]=
In[283]:=
Show[lsplot, Table[ListPlot[ Transpose[{locations, Normal[resampledStates["support"] // Normal][[All, i, 1]]}], PlotStyle -> Orange], {i, numParticles}], Frame -> True, GridLines -> Automatic]
Out[283]=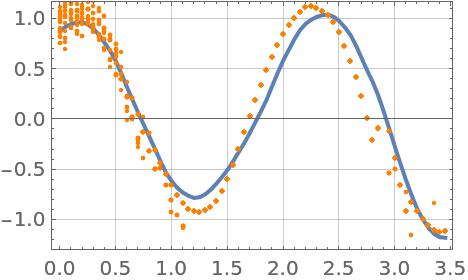
In[284]:=
DeleteObject[p["Session"]]
Solving ODEs (14) 

Set up a Bernoulli equation and its Jacobian:

In[285]:=
session = StartExternalSession["Python"]
Out[285]=
In[286]:=
bernRhs = ResourceFunction["ToPythonFunction"][session, Function[{t, x}, 1.5 (x - x^3)]]
Out[286]=
In[287]:=
bernJac = ResourceFunction["ToPythonFunction"][session, Function[{t, x}, {1.5 (1 - 3 x^2)}], Epilog -> "np.array"]
Out[287]=

Construct an initial value problem:

In[288]:=
p = ResourceFunction["ProbNumObject"][session]
Out[288]=
In[289]:=
{t0, tmax} = {0.0, 6.0}; y0 = {0.};
In[290]:=
bernoulli = p["InitialValueProblem"[bernRhs, t0, tmax, y0, "Df" -> bernJac]]
Out[290]=

Use integrator as a dynamics model:

In[291]:=
dynamicsModel = p["IntegratedWienerTransition"[2, 1, "ForwardImplementation" -> "sqrt"]]
Out[291]=

Add a small “evaluation variance" to the initial random variable:

In[292]:=
initmean = {0, 0, 0}; initcov = 0.0125*DiagonalMatrix[{1, 1.0, 1.0}];
In[293]:=
initialRv = p["Normal"[initmean, initcov, "CovarianceCholesky" -> Sqrt[initcov]]]
Out[293]=
In[294]:=
odePrior = p["MarkovProcess"[0., initialRv, dynamicsModel]]
Out[294]=

Construct an importance distribution using the extended Kalman filter:

In[295]:=
fromEKF = p["LinearizationImportanceDistribution"]["FromEKF"]
Out[295]=
In[296]:=
importance = fromEKF[All][dynamicsModel, "BackwardImplementation" -> "sqrt", "ForwardImplementation" -> "sqrt"]
Out[296]=

Create a particle filter:

In[297]:=
numParticles = 50;
In[298]:=
rng = ResourceFunction["ProbNumObject"][session, "RNG"[123]]
Out[298]=
In[299]:=
odePF = p["ParticleFilter"[odePrior, importance, numParticles, rng]]
Out[299]=

Define a grid of evenly spaced points:

In[300]:=
numLocs = 50;
In[301]:=
locations = Range[0, tmax, tmax/(50 - 1)] // N;

Information operator that measures the residual of an explicit ODE:

In[302]:=
infoOp = p["ODEResidual"[2, 1]]
Out[302]=

Make inference with an information operator using a first-order linearization of the ODE vector-field:

In[303]:=
ek1 = p["EK1"[]]
Out[303]=

Define a regression problem:

In[304]:=
regressionProblem = p["IVPToRegressionProblem"[ bernoulli, locations, infoOp, "ApproximateStrategy" -> ek1, "ExcludeInitialCondition" -> True, "ODEMeasurementVariance" -> 0.00001 ]]
Out[304]=

Find the ODE posterior:

In[305]:=
odePF["Filter"][All][regressionProblem]
Out[305]=
In[306]:=
odePosterior = Normal[%][[1]]
Out[306]=

Resample removing the unlikely particles:

In[307]:=
resampledStates = odePosterior["states"]["resample"[rng]]
Out[307]=

Plot the solution. Depending on the position of the initial particle, the trajectories deviate from the unstable equilibrium at 0 and approach either of the stable equilibria, +1 or -1:

In[308]:=
Show[Table[ ListPlot[ Transpose[{locations, Normal[resampledStates["support"] // Normal][[All, i, 1]]}], PlotMarkers -> {"OpenMarkers", Small}], {i, numParticles}], PlotRange -> All]
Out[308]=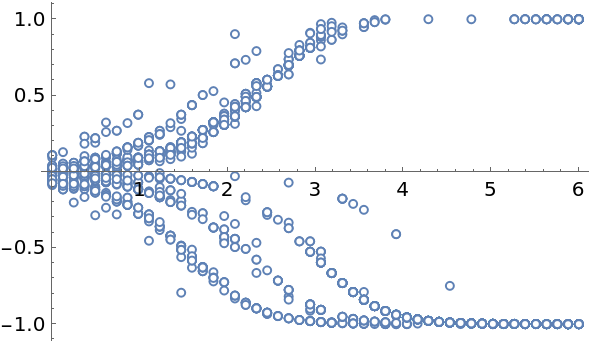

For comparison, solve the equation with DSolve:

In[309]:=
sol = DSolve[y'[t] == 1.5 (y[t] - y[t]^3), y, t]
Out[309]=
In[310]:=
Plot[Evaluate[Table[y[t] /. sol /. C[1] -> c, {c, {2, 5, 10}}]], {t, 0, 6}]
Out[310]=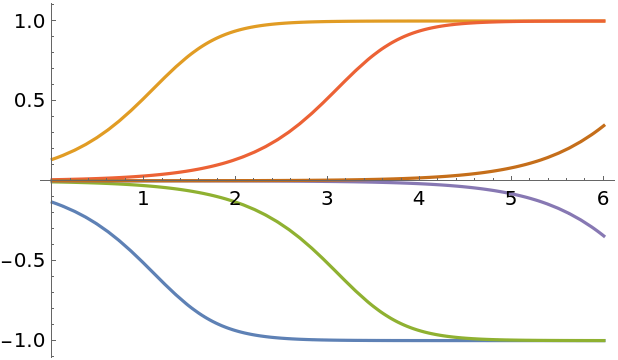
In[311]:=
DeleteObject[session]

Properties and Relations (4) 

ProbNumObject[…] gives the same result as the resource function PythonObject with a special configuration:

In[312]:=
session = StartExternalSession["Python"]
Out[312]=
In[313]:=
ResourceFunction["ProbNumObject"][session]
Out[313]=
In[314]:=
ResourceFunction["PythonObject"][session, "probnum", "Configuration" -> ResourceFunction["ProbNumObject"]]
Out[314]=
In[315]:=
DeleteObject[session]

Available functions:

In[316]:=
p = ResourceFunction["ProbNumObject"][]
Out[316]=
In[317]:=
p["FullInformation", "Functions"]
Out[317]=

Information on a function:

In[318]:=
p["Information", "ProbabilisticLinearSolve"]
Out[318]=

Search the web documentation for a function in your default browser:

In[319]:=
p["WebInformation", "ProbabilisticLinearSolve"] // SystemOpen
In[320]:=
DeleteObject[p["Session"]]

Find a Wolfram language name for a Python-side function:

In[321]:=
p = ResourceFunction["ProbNumObject"][]
Out[321]=
In[322]:=
p["FromPythonName", "problinsolve"]
Out[322]=

Or a Python name corresponding to a Wolfram-Language name:

In[323]:=
p["ToPythonName", %]
Out[323]=

The list of conversion rules:

In[324]:=
p["RenamingRules"] // Short
Out[324]=
In[325]:=
DeleteObject[p["Session"]]

Solve a linear matrix equation with LinearSolve:

In[326]:=
a = {{7.5, 2., 1.}, {2., 2., 0.5}, {1., 0.5, 5.5}}; b = {1., 2., -3.};
In[327]:=
x = LinearSolve[a, b]
Out[327]=

Solve the same equation with ProbNum:

In[328]:=
p = ResourceFunction["ProbNumObject"][]
Out[328]=
In[329]:=
solution = p["ProbabilisticLinearSolve"[a, b]] // Normal
Out[329]=

The multivariate Gaussian random variable corresponding to the solution:

In[330]:=
xRV = solution[[1]]
Out[330]=

The mean of the normal distribution equals the best guess for the solution of the linear system:

In[331]:=
xRV["mean"] // Normal // Normal
Out[331]=
In[332]:=
% == x
Out[332]=

The covariance matrix provides a measure of uncertainty:

In[333]:=
xRV["cov"]["ToDense"[]] // Normal // Normal
Out[333]=

In this case, the algorithm is very certain about the solution as the covariance matrix is virtually zero:

In[334]:=
Chop[%]
Out[334]=

Clean up by closing the Python session:

In[335]:=
DeleteObject[p["Session"]]

Neat Examples (2) 

Display the first few matrices from the SuiteSparse Matrix Collection:

In[336]:=
p = ResourceFunction["ProbNumObject"][]
Out[336]=
In[337]:=
first10 = {"1138_bus", "494_bus", "662_bus", "685_bus", "abb313", "arc130", "ash219", "ash292", "ash331", "ash608"};

Install the requests module, if it's not yet installed in your Python:

In[338]:=
ResourceFunction["PythonPackageInstall"][p["Session"], "requests"]
Out[338]=
In[339]:=
data = Function[m, Normal[m[#]] & /@ {"matid", "name", "group", "kind", "shape", "A"}] /@ (p["SuiteSparseMatrix"[#, "HB"]] & /@ Take[first10, 7]);
In[340]:=
Text@Grid[ Prepend[data /. sp_SparseArray :> MatrixPlot[sp], {"ID", "Name", "Group", "Kind", "Shape", ""}], Background -> {None, {Lighter[Yellow, .5], {White, Lighter[LightGreen, .5]}}}, Dividers -> Gray, ItemSize -> {{3, 7, 5, 10}}, Frame -> Gray, Spacings -> {Automatic, .8}, ItemStyle -> 14]
Out[340]=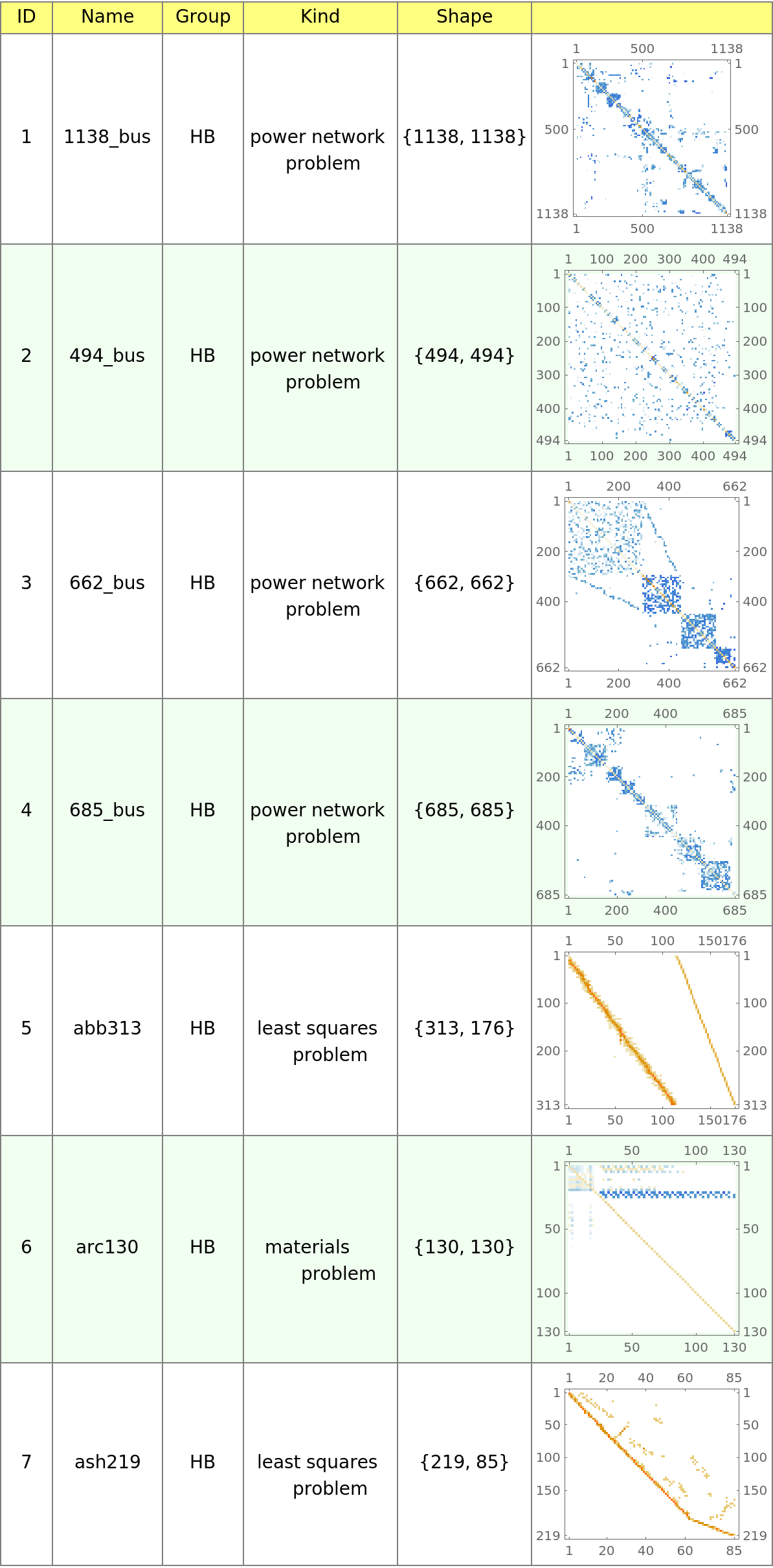
In[341]:=
DeleteObject[p["Session"]]

Version History

  • 1.1.0 – 24 June 2022
  • 1.0.0 – 01 April 2022

Source Metadata

  • Citation:

Related Resources

Author Notes

Signatures of LTIGaussian and NonlinearGaussian changed in ProbNum v. 0.1.17. If the related examples in the Applications section fail for you with:

… update your ProbNum to a more recent version. To check the version:

In[1]:=
p = ProbNumObject[]
In[2]:=
p["__version__"]
In[3]:=
DeleteObject[p["Session"]]

License Information