Function Repository Resource:

PrincipalAxisClustering

Source Notebook

Quickly cluster a point cloud by recursive separation

Contributed by: Richard Hennigan (Wolfram Research)

ResourceFunction["PrincipalAxisClustering"][{{p₁₁,p₁₂,…},{p₂₁,p₂₂,…},…}]

recursively partitions the given points into approximately equal-sized clusters along their principal axis.

ResourceFunction["PrincipalAxisClustering"][points,n]

partitions points into at most n clusters.

Details and Options

ResourceFunction["PrincipalAxisClustering"][points] is equivalent to ResourceFunction["PrincipalAxisClustering"][points,Automatic].

If n is a power of 2, the clusters will be approximately equal-sized.

ResourceFunction["PrincipalAxisClustering"] accepts a Method option, which decides how to separate points according to their projected values on the principal axis.

The value for Method can be one of the following:

Median

separate points into approximately equal-sized clusters

Mean

separate points at the center of mass

Examples

Basic Examples (3)

Cluster one-dimensional data:

In[1]:=

Out[1]=

Find exactly four clusters:

In[2]:=

Out[2]=

Cluster vectors of real values:

In[3]:=

Out[3]=

Scope (2)

Partition a 3D point cloud:

In[4]:=

Out[4]=

In[5]:=

Out[5]=

Cluster high-dimensional data:

In[6]:=

Out[6]=

Options (3)

Method (3)

With the default setting of Method→Median, clusters are likely to span across gaps:

In[7]:=

Out[7]=

In[8]:=

Out[8]=

Using Method→Mean can improve separation:

In[9]:=

Out[9]=

However, Mean will tend to produce unbalanced cluster sizes compared to Median:

In[10]:=

Out[10]=

In[11]:=

Out[11]=

Applications (2)

Downsample a large point cloud by choosing nicely spaced representative points:

In[12]:=

In[13]:=

Out[13]=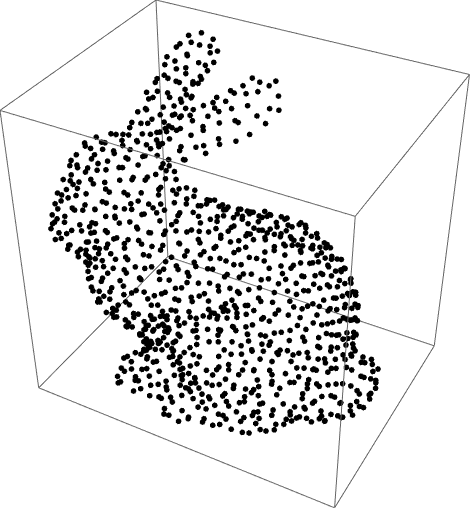

Compare to random sampling:

In[14]:=

Out[14]=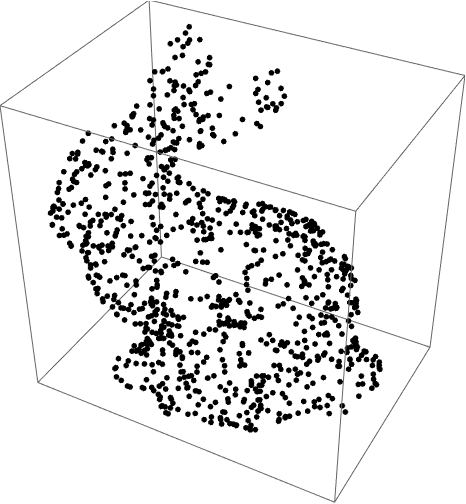

Properties and Relations (4)

The axis representing each cluster separation corresponds to the first component in PrincipalComponents:

In[15]:=

$points = N[Position[ImageData[\!$\* GraphicsBox[ TagBox[RasterBox[CompressedData[" 1:eJzd2UFOw0AMBdCYFUuuwC3YsmTbigO0IlRsgkiRELcnLCmZsf//zoQQqZWq jv8bO60StbfH193zVdd15+vpaXf4uB/Hw+f+ZnrxOJxfTkP/9DC896d+vDt+ L9tPj7fuDxxmrT1rS5om4sUJIFRtpolwdQ4IlIugwfWrgaS4Hhiu10DbEkiJ GwCJLWrVJon/HmSKFdBUEBVbg6aDmJgBUvcKUKWtDTI3J0jhL4+5kIrgsme/ NTjnsaef98jpCB5VrXmRhHTQy4BB13NiUDDkVYKwccS9YhQIAl4hDAPnMiEz tilvd3HS31ENrOaEF0ZBb1LzqTToNV/KRcHajyueaBwYab9Mlltfiiy23lZc dq7Z5Iaa5MUVPjwkqYgUKYEEKXo4qYMYmeEhZJIXJfO4qJhqthaDXh4ZB9t/ NXQS1GSR8DSSA7ckkp7+/1IbMZCYKsY6SBPr3I+4DNHjLuJkMOBd5GliAXDi aLDcjxtHgbXZBNJQsKJdvF9PiFjzXmlJJSOKzYDlVUhoVEzLjJGtuNzjCyxr GaM= "], {{0, 83}, {113, 0}}, {0, 1}, ColorFunction->GrayLevel], BoxForm`ImageTag["Bit", ColorSpace -> Automatic, Interleaving -> None], Selectable->False], BaseStyle->"ImageGraphics", ImageSizeRaw->{113, 83}, PlotRange->{{0, 113}, {0, 83}}]$], 1, {2}]];$

In[16]:=

Out[16]=

In[17]:=

Out[17]=

The principal axis can be obtained from the Eigenvectors of the Covariance matrix:

In[18]:=

Out[18]=

Visualize the axis over the original data:

In[19]:=

Out[19]=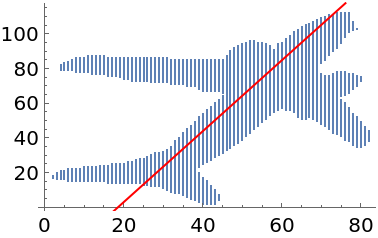

Projecting the standardized points onto the principal axis gives scalar values that indicate which cluster they belong to:

In[20]:=

Out[20]=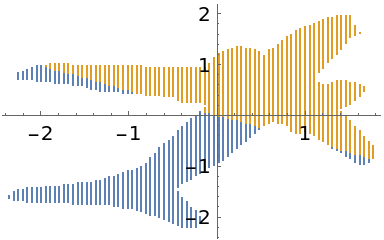

PrincipalAxisClustering finds clusters very quickly:

In[21]:=

Out[21]=

In[22]:=

Out[22]=

Compare to FindClusters:

In[23]:=

Out[23]=

PrincipalAxisClustering gives clusters that better represent the local point cloud density:

In[24]:=

Out[24]=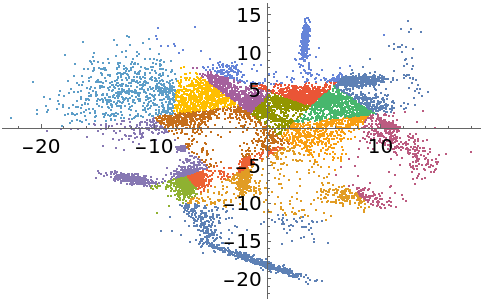

FindClusters represents better separation of the data:

In[25]:=

Out[25]=

PrincipalAxisClustering partitions points into non-overlapping convex regions:

In[26]:=

In[27]:=

Out[27]=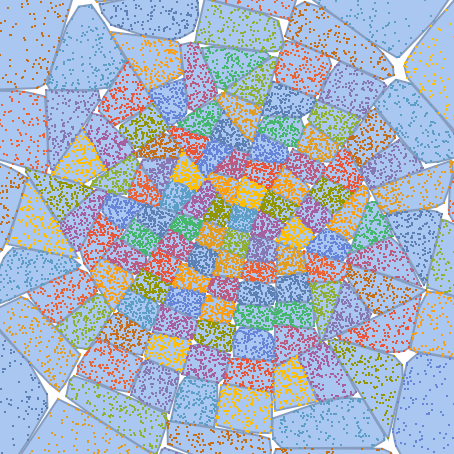

The number of clusters locally scales with the point cloud density:

In[28]:=

Out[28]=

In[29]:=

Out[29]=

Possible Issues (1)

If the number of requested clusters is not a power of 2, then cluster sizes will not be well balanced:

In[30]:=

In[31]:=

Out[31]=

In[32]:=

Out[32]=

Neat Examples (2)

Visualize the recursive nature of the clustering:

In[33]:=

$data = RandomReal[{-1, 1}, {10^4, 2}];$

In[34]:=

$plots = Table[ ListPlot[ResourceFunction["PrincipalAxisClustering"][data, 2^n], Sequence[ AspectRatio -> 1, Frame -> True, Axes -> False, FrameTicks -> None]], {n, 0, 5}];$

In[35]:=

Out[35]=

Partition a point cloud into clusters:

In[36]:=

Out[36]=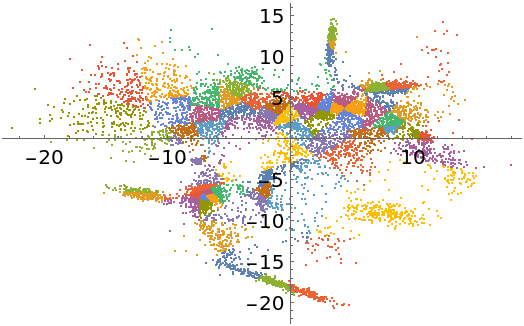

Remove some outliers from each cluster:

In[37]:=

$filterOutliers[cluster_, q_] := Module[{m, d, t}, m = Mean[cluster]; d = Norm[# - m] & /@ cluster; t = Quantile[d, 1 - q]; Pick[cluster, # < t & /@ d] ];$

In[38]:=

In[39]:=

$expand[cluster_, s_] := With[{m = Mean[cluster]}, m + s (# - m) & /@ cluster ];$

Construct a parameterized topological representation of the point cloud:

In[40]:=

Out[40]=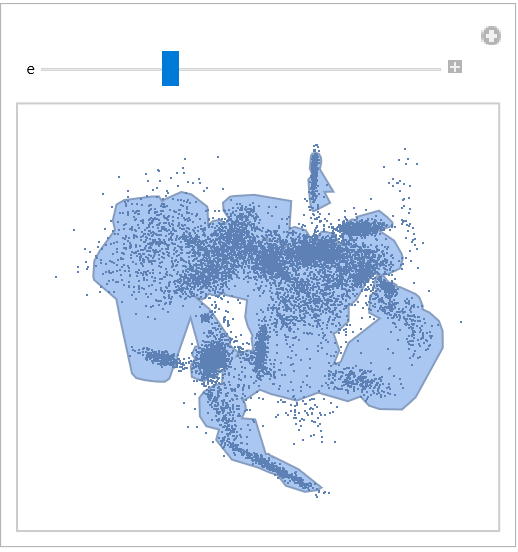

Version History

1.0.0 – 03 January 2022

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

PrincipalAxisClustering

Details and Options