Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the primorial
ResourceFunction["Primorial"][n] calculates the product of the primes up to n. |
Compute the primorial ![]() :
:
| In[1]:= |
| Out[1]= |
Compute a list of the first 15 primorials:
| In[2]:= |
| Out[2]= |
For non-positive numbers, the primorial is defined to be equal to 1:
| In[3]:= |
| Out[3]= |
Compare with the definition:
| In[4]:= |
| Out[4]= |
The resource function ChebyshevTheta is the logarithm of the primorial:
| In[5]:= |
| Out[5]= |
Evaluate the infinite primorial:
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= |
Compare the growth rate of the primorial to that of the factorial:
| In[8]:= | ![DiscretePlot[{ResourceFunction["Primorial"][n], Factorial[n]}, {n, 1, 50}, ScalingFunctions -> "Log", PlotLegends -> {"n#", "n!"}]](https://www.wolframcloud.com/obj/resourcesystem/images/1ba/1ba58f96-8745-419b-bb21-04c24efbf6e2/10245725a8634a12.png) |
| Out[8]= | 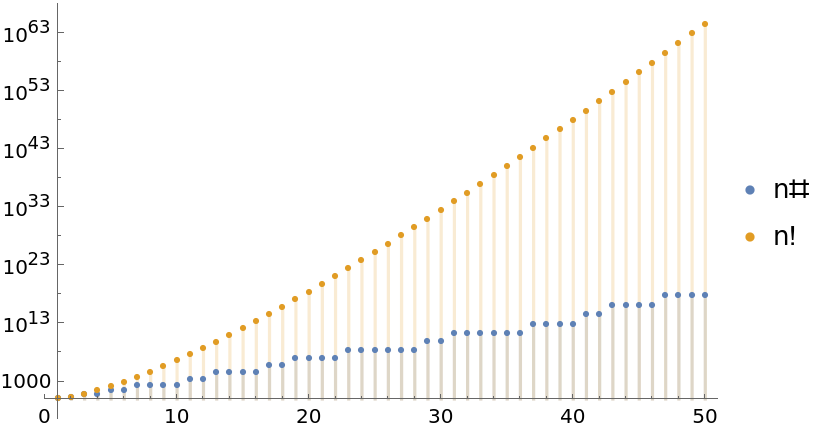 |
Plot the differences between the factorial and the primorial up to n:
| In[9]:= |
| Out[9]= | 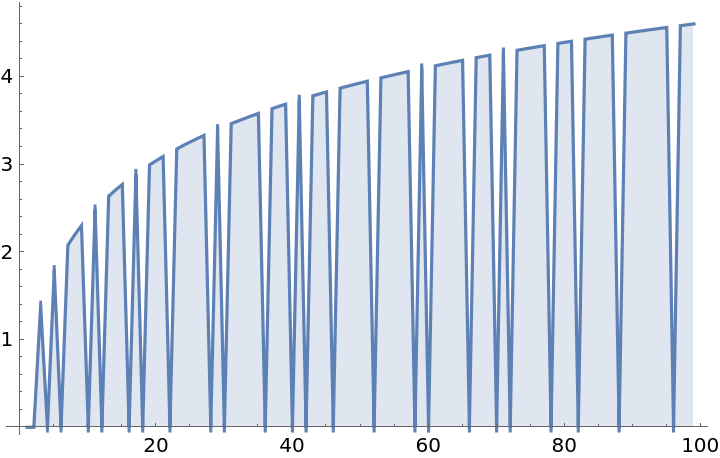 |
This work is licensed under a Creative Commons Attribution 4.0 International License