Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PowerTriangulation

Source Notebook

Generate the power triangulation of a set of circles

Contributed by: Jan Mangaldan

ResourceFunction["PowerTriangulation"][{c1,c2,…}]

gives a MeshRegion representing the power triangulation of the circles c1,c2, ….

Details

The circles ci can be Circle or Disk objects.
Point objects are treated as circles with zero radius.
A power triangulation is also known as Laguerre triangulation or Laguerre–Delaunay triangulation; it generalizes the Delaunay triangulation.
A power triangulation can be considered as a weighted Delaunay triangulation of the circles' centers, with the radii of the circles as weights.
A power triangulation consists of triangles (in 2D) and n-dimensional simplices (in nD).
An nD power triangulation has simplex cells defined by n+1 circle centers, such that the circumsphere for the same n+1 points contains no other circle centers from the original circles ci.
ResourceFunction["PowerTriangulation"] takes the same options as MeshRegion.

Examples

Basic Examples (2) 

Generate the power triangulation of a set of circles:

In[1]:=
circles = Table[Circle[RandomVariate[NormalDistribution[], 2], RandomReal[{0, 1/2}]], {10}]; \[ScriptCapitalR] = ResourceFunction["PowerTriangulation"][circles]
Out[1]=

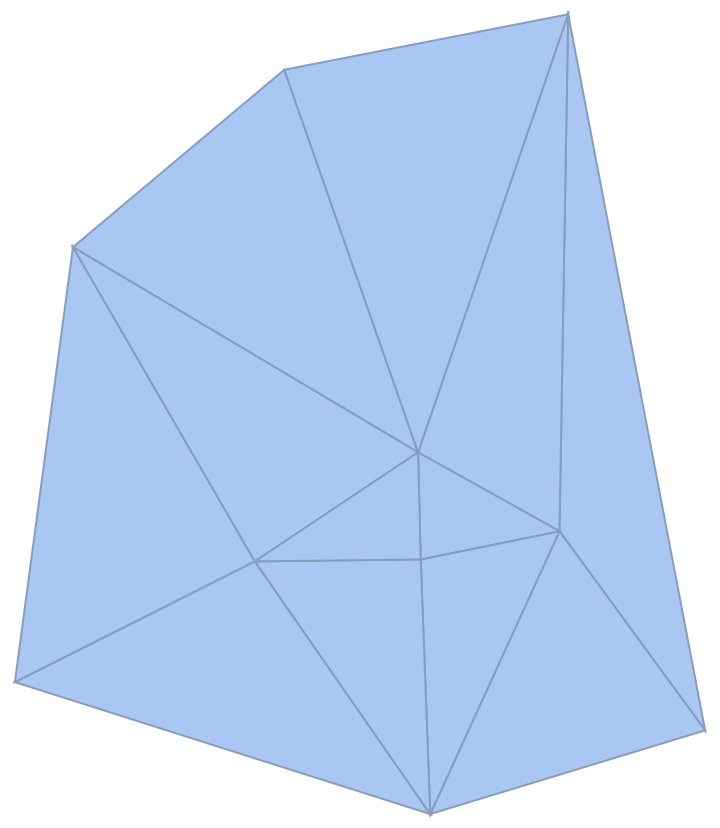
Show the power triangulation with the generating circles:

In[2]:=
Show[\[ScriptCapitalR], Graphics[{Orange, circles}]]
Out[2]=

Scope (2) 

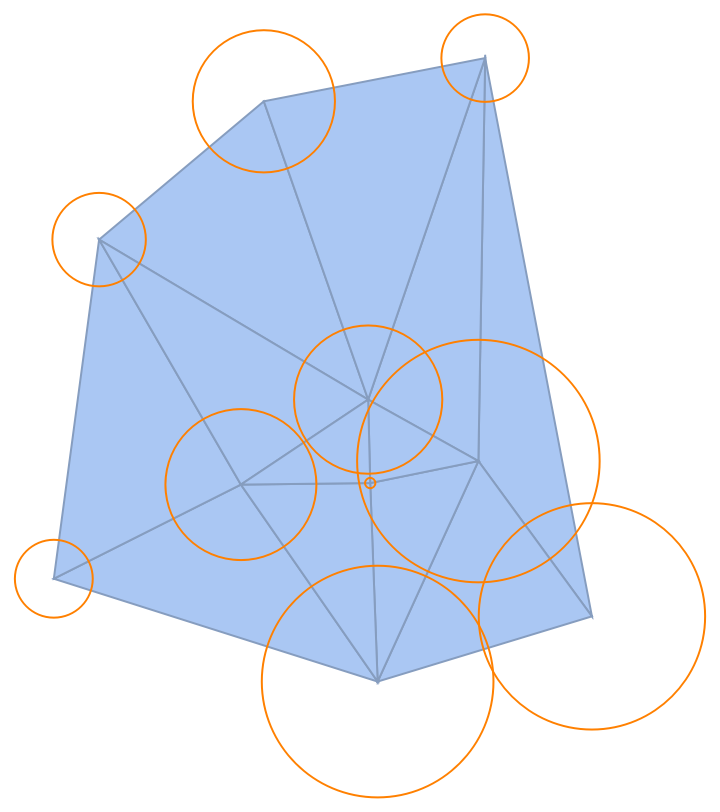
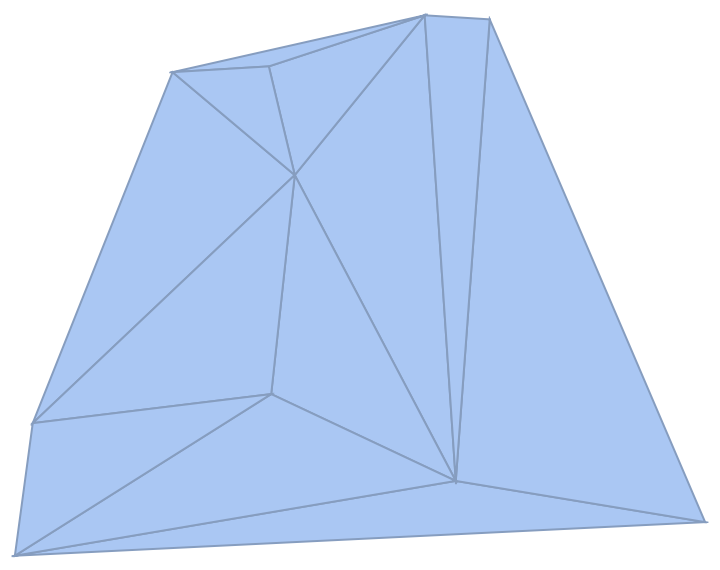
Create a power triangulation from a set of disks:

In[3]:=
cl = Table[Disk[RandomReal[{-2, 2}, {2}], RandomReal[{0, 1/4}]], {20}]; \[ScriptCapitalR] = ResourceFunction["PowerTriangulation"][cl]
Out[4]=

Basic properties:

In[5]:=
{RegionQ[\[ScriptCapitalR]], MeshRegionQ[\[ScriptCapitalR]]}
Out[5]=

Power triangulations are full dimensional:

In[6]:=
{RegionDimension[\[ScriptCapitalR]], RegionEmbeddingDimension[\[ScriptCapitalR]]}
Out[6]=

Power triangulations are bounded:

In[7]:=
{BoundedRegionQ[\[ScriptCapitalR]], RegionBounds[\[ScriptCapitalR]]}
Out[7]=

Find its area and centroid:

In[8]:=
{RegionMeasure[\[ScriptCapitalR]], RegionCentroid[\[ScriptCapitalR]]}
Out[8]=

Test for point membership or distance to the closest point in the region:

In[9]:=
RegionMember[\[ScriptCapitalR], {0.5, 0.5}]
Out[9]=
In[10]:=
{RegionDistance[\[ScriptCapitalR], {2, 2}], RegionNearest[\[ScriptCapitalR], {2, 2}]}
Out[10]=

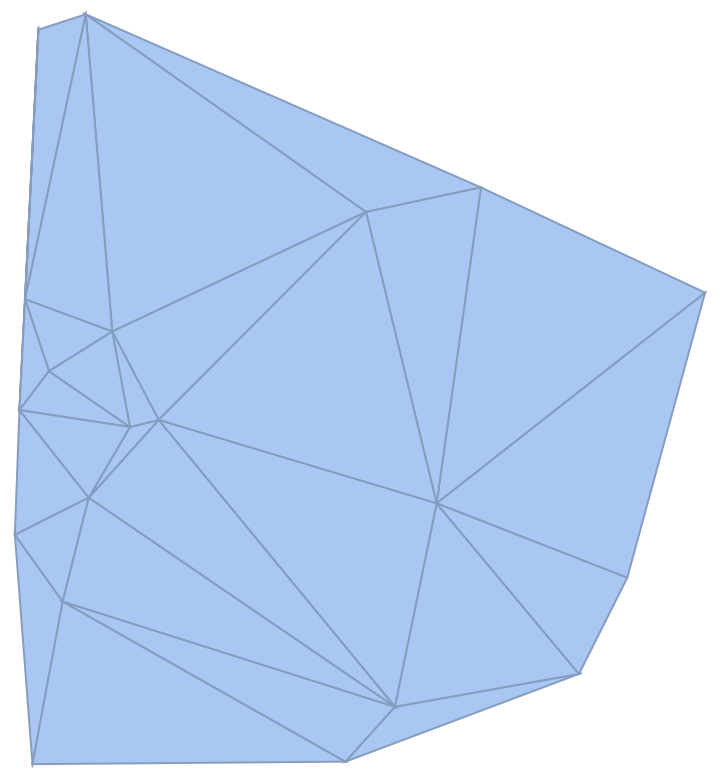
Generate the power triangulation of a mixture of Circle and Disk objects:

In[11]:=
cl = Table[ RandomChoice[{Circle, Disk}][ RandomVariate[NormalDistribution[], 2], RandomReal[{0, 1/2}]], {10}]; ResourceFunction["PowerTriangulation"][cl]
Out[11]=

Options (10) 

MeshCellHighlight (2) 

MeshCellHighlight allows you to specify highlighting for parts of a PowerTriangulation:

In[12]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellHighlight -> {{1, All} -> Red, {0, All} -> Black}]
Out[12]=

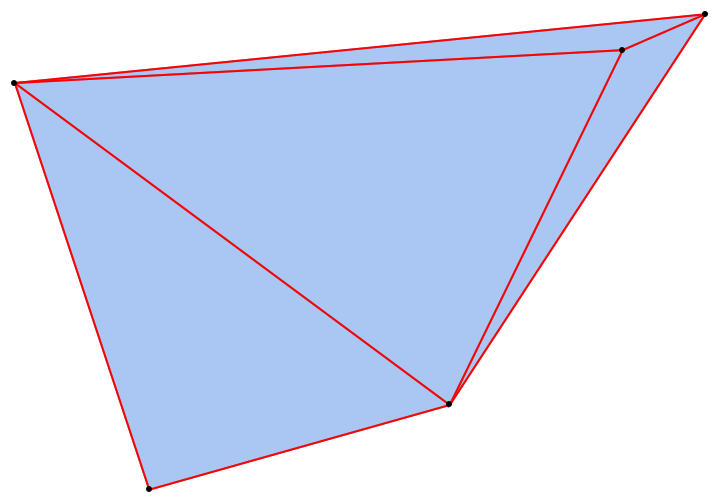
Individual cells can be highlighted using their cell index:

In[13]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellHighlight -> {{1, 1} -> {Thick, Red}, {1, 2} -> {Dashed, Black}}]
Out[13]=

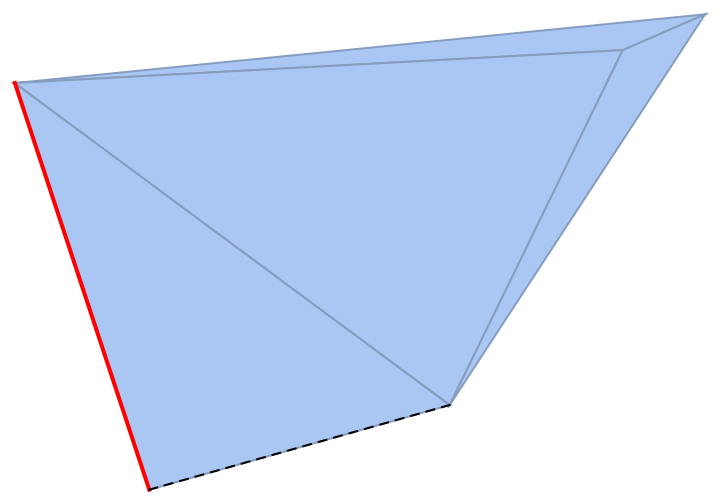
Or by the cell itself:

In[14]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellHighlight -> {Line[{1, 2}] -> {Thick, Red}, Line[{2, 3}] -> {Dashed, Black}}]
Out[14]=

MeshCellLabel (2) 

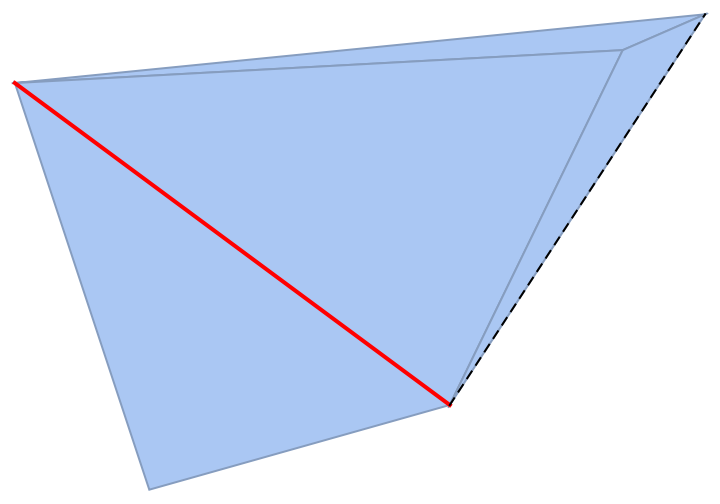
MeshCellLabel can be used to label parts of a PowerTriangulation:

In[15]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellLabel -> {0 -> "Index"}]
Out[15]=

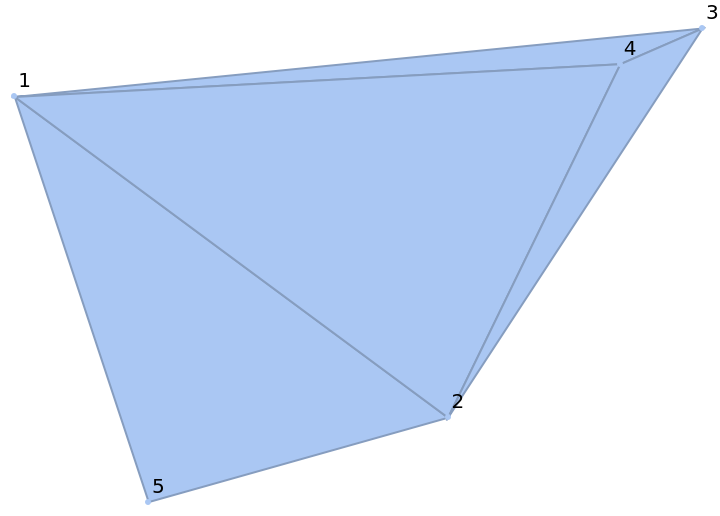
Individual cells can be labeled using their cell index:

In[16]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellLabel -> {{1, 1} -> "x", {1, 2} -> "y"}]
Out[16]=

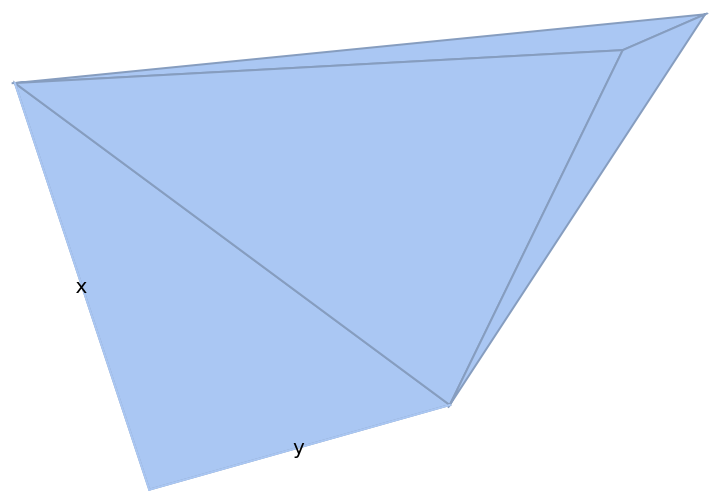
Or by the cell itself:

In[17]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellLabel -> {Line[{1, 3}] -> "x", Line[{1, 2}] -> "y"}]
Out[17]=

MeshCellMarker (2) 

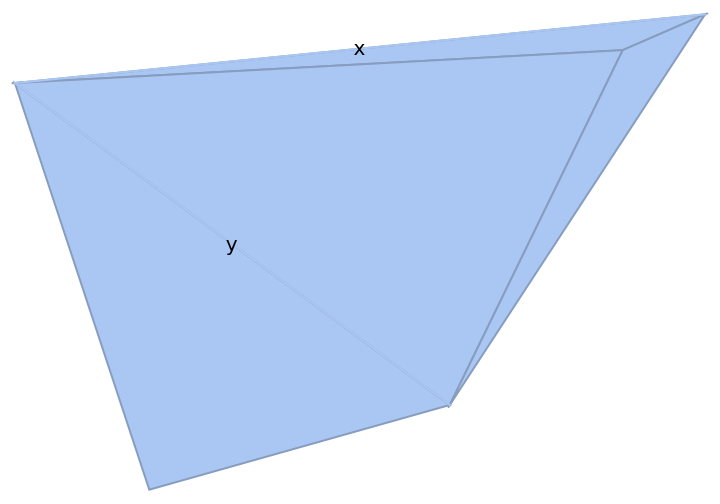
MeshCellMarker can be used to assign values to parts of a PowerTriangulation:

In[18]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellMarker -> {{0, 1} -> 1, {0, 2} -> 2, {0, 3} -> 3, {0, 4} -> 4, {0, 5} -> 5}]
Out[18]=

Use MeshCellLabel to show the markers:

In[19]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellMarker -> {{0, 1} -> 1, {0, 2} -> 2, {0, 3} -> 3, {0, 4} -> 4, {0, 5} -> 5}, MeshCellLabel -> {0 -> "Marker"}]
Out[19]=

MeshCellStyle (2) 

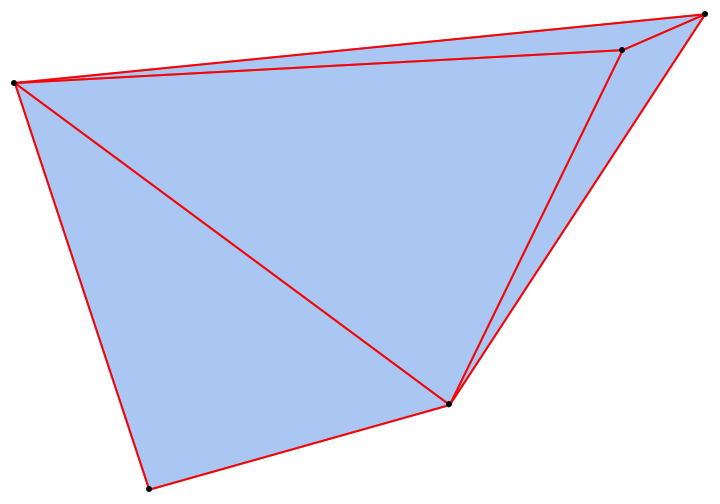
MeshCellStyle allows you to specify styling for parts of a PowerTriangulation:

In[20]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellStyle -> {{1, All} -> Red, {0, All} -> Black}]
Out[20]=

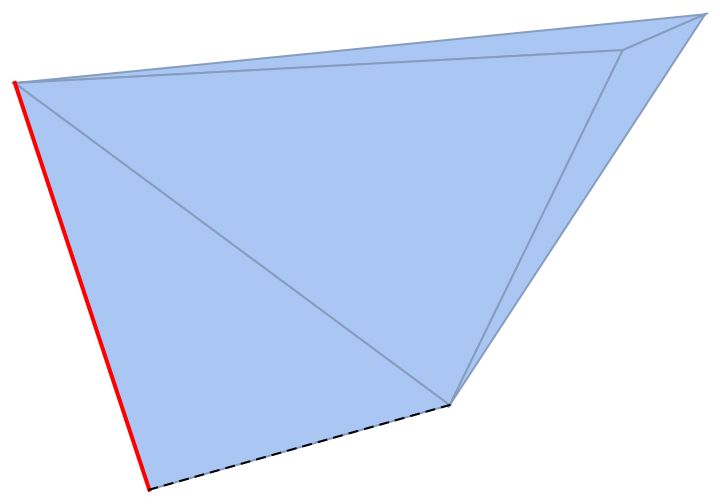
Individual cells can be highlighted using their cell index:

In[21]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellStyle -> {{1, 1} -> {Thick, Red}, {1, 2} -> {Dashed, Black}}]
Out[21]=

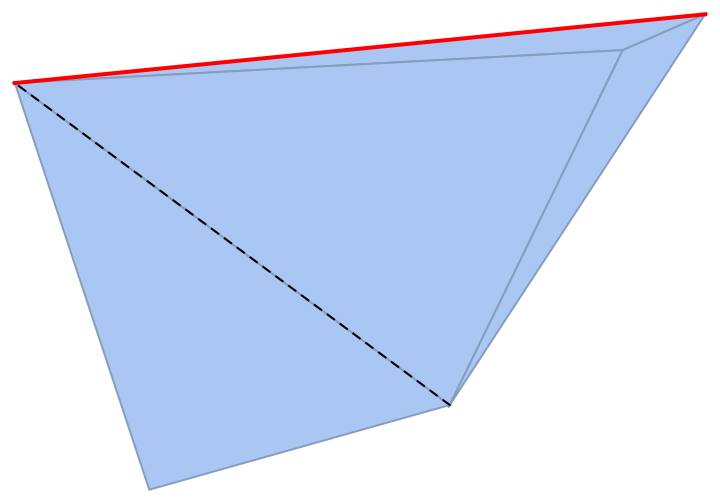
Or by the cell itself:

In[22]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {5}], MeshCellStyle -> {Line[{1, 3}] -> {Thick, Red}, Line[{1, 2}] -> {Dashed, Black}}]
Out[22]=

PlotTheme (2) 

Use a theme with grid lines and a legend:

In[23]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {10}], PlotTheme -> "Detailed"]
Out[23]=

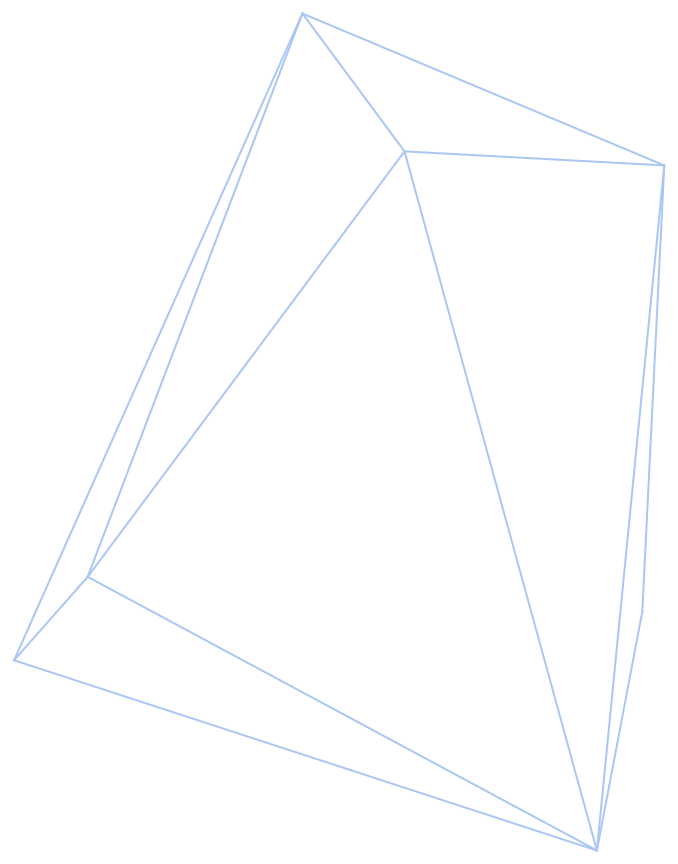
Use a theme to draw a wireframe:

In[24]:=
ResourceFunction["PowerTriangulation"][ Table[Disk[RandomReal[1, 2], RandomReal[]], {10}], PlotTheme -> "Lines"]
Out[24]=

Properties and Relations (4) 

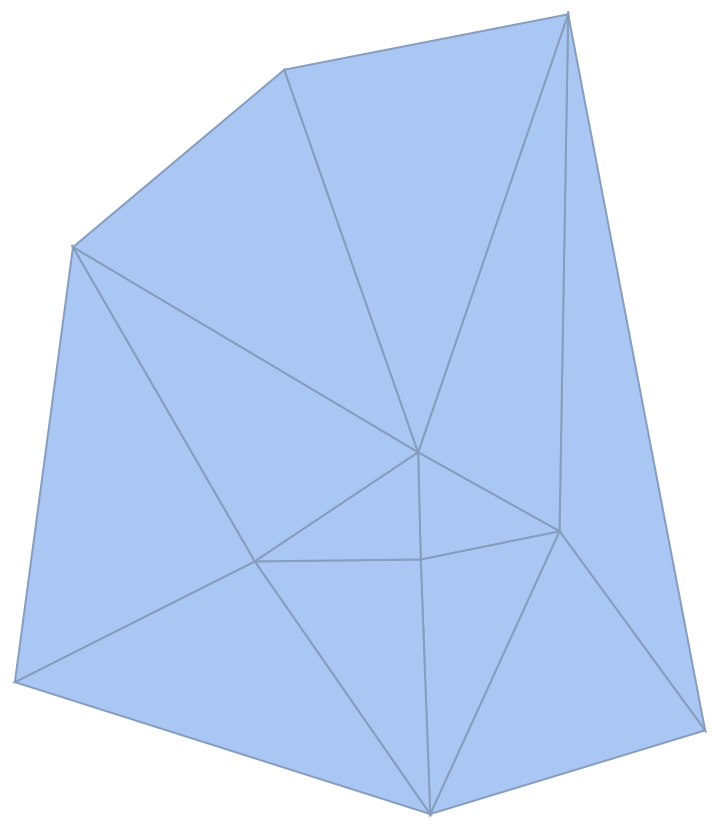
The output of PowerTriangulation is always a full-dimensional MeshRegion:

In[25]:=
circles = Table[Circle[RandomVariate[NormalDistribution[], 2], RandomReal[{0, 1/2}]], {10}]; ResourceFunction["PowerTriangulation"][circles]
Out[25]=
In[26]:=
{MeshRegionQ[%], RegionDimension[%]}
Out[26]=

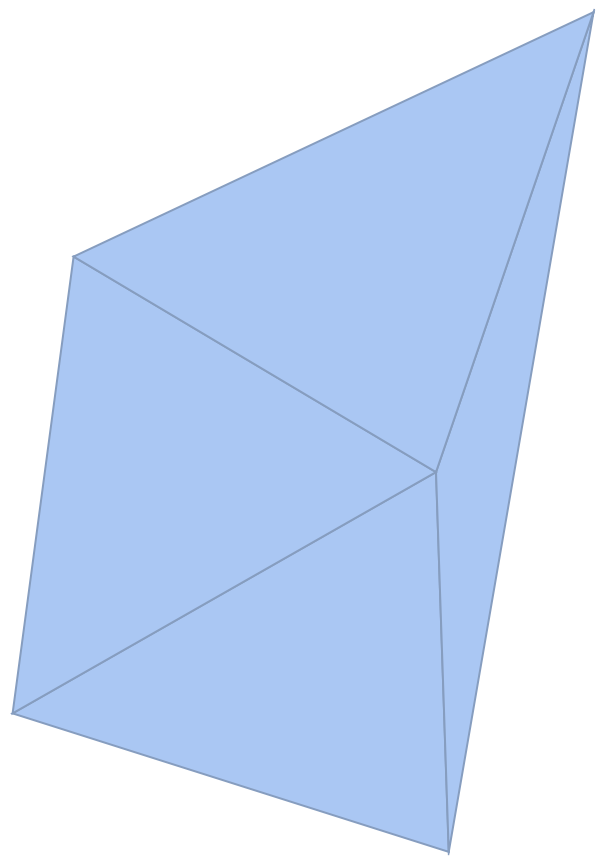
The circumcircle for each triangle in a power triangulation contains no other circles' centers:

In[27]:=
circles = Table[Circle[RandomVariate[NormalDistribution[], 2], RandomReal[{0, 1/2}]], {5}]; \[ScriptCapitalR] = ResourceFunction["PowerTriangulation"][circles]
Out[27]=

Find circumcircles for all triangles:

In[28]:=
circum = Circumsphere @@@ Normal@GraphicsComplex[MeshCoordinates[\[ScriptCapitalR]], MeshCells[\[ScriptCapitalR], 2]];

Plot the circumcircles as disks:

In[29]:=
Show[HighlightMesh[\[ScriptCapitalR], Style[0, PointSize[Large]]], Graphics[{Orange, circum}], PlotRange -> 2]
Out[29]=

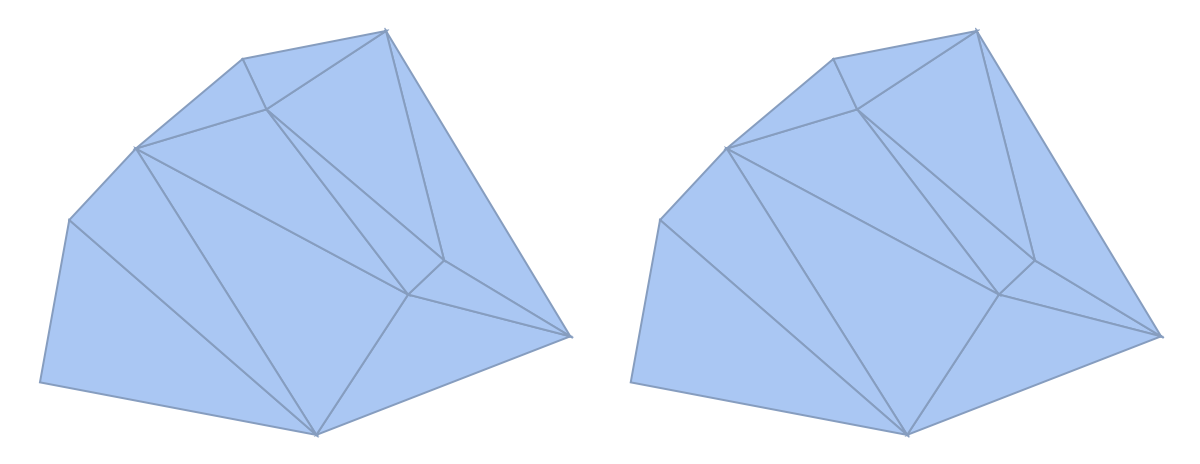
The power triangulation of a set of circles all having the same radii is equivalent to the DelaunayMesh of the circles' centers:

In[30]:=
circles = Table[Circle[RandomVariate[NormalDistribution[], 2], 0.4], {10}]; GraphicsRow[{ResourceFunction["PowerTriangulation"][circles], DelaunayMesh[First /@ circles]}]
Out[30]=

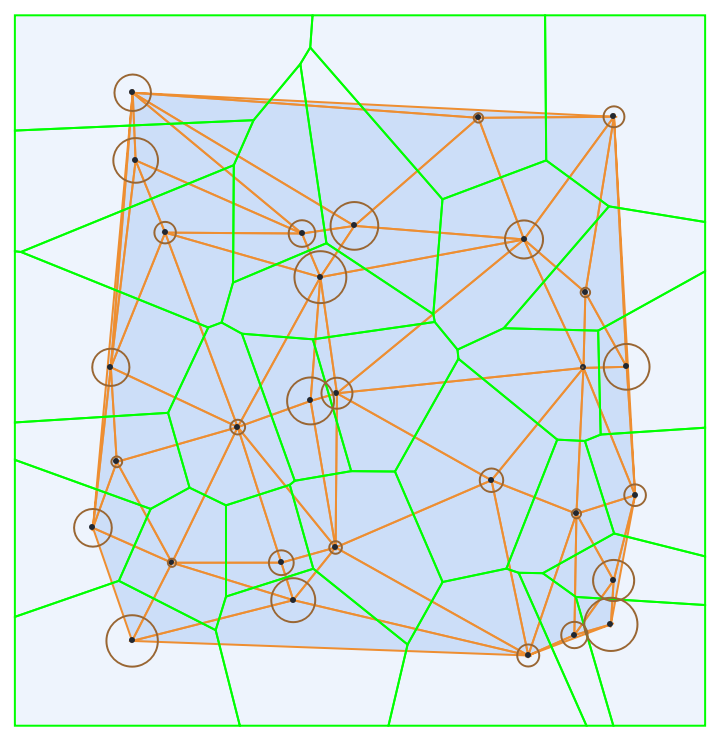
The resource function PowerDiagram is the dual of PowerTriangulation:

In[31]:=
circles = Table[Circle[RandomReal[{-7/2, 7/2}, 2], RandomReal[1/3]], {30}]; pt = HighlightMesh[ ResourceFunction["PowerTriangulation"][circles], {Style[0, Black], Style[1, Orange], Style[2, Opacity[0.5]]}]; pd = HighlightMesh[ ResourceFunction["PowerDiagram"][circles], {Style[1, Green], Style[2, Opacity[0.2]]}]; Show[pt, pd, Graphics[{Brown, circles}]]
Out[32]=

Version History

  • 1.0.0 – 18 January 2021

Source Metadata

  • Citation:
    • Aurenhammer F., Power Diagrams: Properties, Algorithms and Applications. SIAM Journal on Computing, vol. 16, no. 1, 78–96, 1987.
      DOI: 10.1137/0216006
    • Sugihara K., Three-dimensional convex hull as a fruitful source of diagrams. Theoretical Computer Science, vol. 35, no. 2, 325-337, 2000.
      DOI: 10.1016/S0304-3975(99)00202-9

Related Resources

Author Notes

The current implementation is only limited to the 2D case. An extension to 3D is left for a future update.

License Information