Basic Examples (1) 

Subdivide the range 10–10000 in 3 steps:

In[1]:=

Out[1]=

Scope (3) 

With two arguments, the start of the sequence is assumed to be 1:

In[2]:=

Out[2]=

PowerSubdivide works on symbolic entries:

In[3]:=

Out[3]=

x_min can be larger than x_max:

In[4]:=

Out[4]=

Applications (1) 

PowerSubdivide gives points that are "logarithmically useful" for plotting on a logarithmic scale:

In[5]:=

Out[5]=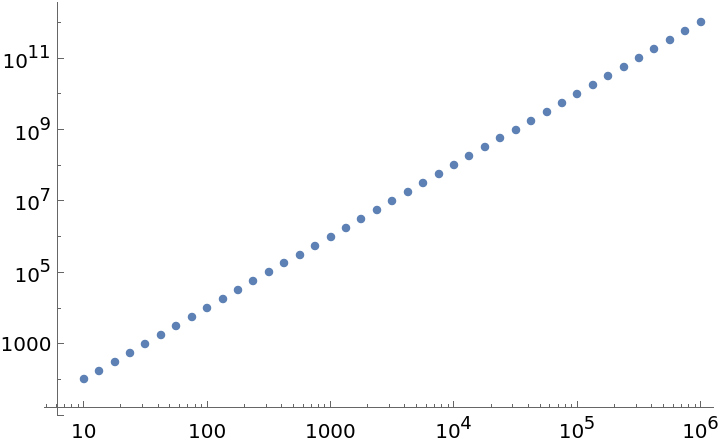

Properties and Relations (4) 

The ratio between subsequent values is constant:

In[6]:=

Out[6]=

PowerSubdivide is related to Subdivide:

In[7]:=

Out[7]=

Negative and positive end points results in intermediate values in the complex plane:

In[8]:=

Out[8]=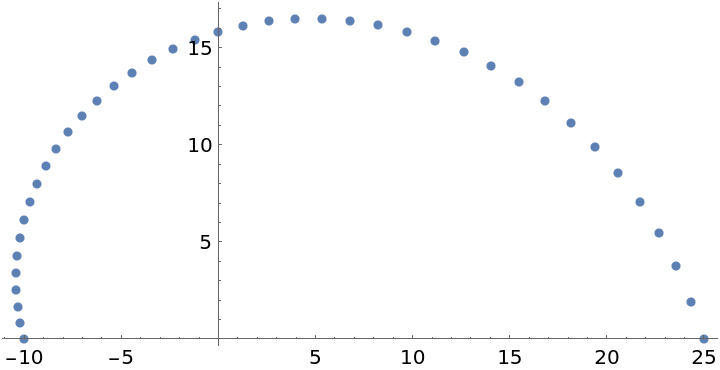

Calculate the geometric mean of two values:

In[9]:=

Out[9]=

Compare to the built-in function:

In[10]:=

Out[10]=

Possible Issues (3) 

If the start or end is a negative number, intermediate values might be complex numbers:

In[11]:=

Out[11]=

If both end points are negative real numbers, Chop might be needed to remove approximate zeros:

In[12]:=

Out[12]=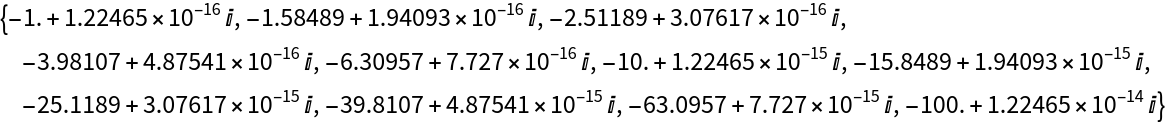

In[13]:=

Out[13]=

Because Log(0) equals -∞, all but the last entry will be 0:

In[14]:=

Out[14]=

Neat Examples (1) 

Connect pairs of random complex numbers:

In[15]:=

Out[16]=