Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the mean of a list of numbers all taken to some power
ResourceFunction["PowerMean"][y,n] represents an operator form of ResourceFunction["PowerMean"] that can be applied to x. | |
ResourceFunction["PowerMean"][y] represents an operator form of ResourceFunction["PowerMean"] that, when applied to x, computes the mean at the top level. | |
ResourceFunction["PowerMean"][] represents an operator form of ResourceFunction["PowerMean"] that, when applied to x, takes the mean of the squares. |
Compute the mean of the squares of a list:
| In[1]:= |
| Out[1]= |
Compute the sum of the cubes of a list with symbolic parts:
| In[2]:= |
| Out[2]= |
Compute the mean of the cubes of a symbolic array:
| In[3]:= |
| Out[3]= |
Create an operator that when confronted with an expression computes the mean of its square roots:
| In[4]:= |
| Out[4]= |
The power may be complex, as may the list:
| In[5]:= |
| Out[5]= |
The level specification can affect the results when the data has more than one dimension:
| In[6]:= |
| Out[6]= |
The default is to apply at level 1:
| In[7]:= |
| Out[7]= | 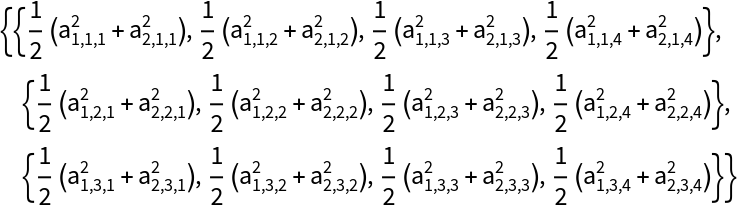 |
Apply the mean down to level 2:
| In[8]:= |
| Out[8]= | 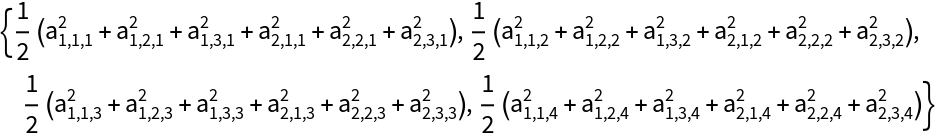 |
Apply the mean in the last two dimensions:
| In[9]:= |
| Out[9]= |
Use PowerMean to conduct ordinary least squares linear regression by finding the values of two parameters a and b that minimize the mean of the squared distances between the actual value of the independent variable and a value that depends on a and b:
| In[10]:= |
| Out[10]= |
Use PowerMean to perform "Tikhonov" (ridge) regression:
| In[11]:= | ![Quiet@Minimize[{ResourceFunction["PowerMean"][2][
Map[5 # - 6 &][{3, 4, 5}] - Map[a *# + b &][{3, 4, 5}]], ResourceFunction["PowerMean"][2][{a, b}] < 29}, {a, b}] // N](https://www.wolframcloud.com/obj/resourcesystem/images/279/279db430-553d-4aef-b547-c6676b60c358/0e8ebffa2cee9a88.png) |
| Out[11]= |
Use PowerMean to perform "LASSO" regression:
| In[12]:= | ![Quiet@Minimize[{ResourceFunction["PowerMean"][2][
Map[5 # - 6 &][{3, 4, 5}] - Map[a *# + b &][{3, 4, 5}]], ResourceFunction["PowerMean"][1][Abs@{a, b}] < 5}, {a, b}] // N](https://www.wolframcloud.com/obj/resourcesystem/images/279/279db430-553d-4aef-b547-c6676b60c358/23f78bb0f9a0f5d9.png) |
| Out[12]= |
PowerMean[] is the same as the mean square of the results from the Norm function if the arguments it confronts are real-valued, but is not necessarily the same if the values it confronts are complex:
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
This work is licensed under a Creative Commons Attribution 4.0 International License