Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Determine if a set of coordinates is partially ordered
ResourceFunction["PosetQ"][poset] determines if the coordinates in poset are partially ordered. |
Test various posets:
| In[1]:= |  |
| In[2]:= |
| Out[3]= |
Test various non-posets:
| In[4]:= |
| Out[4]= |
For PosetQ, posets must be comprised of integers:
| In[5]:= |
| Out[5]= |
For PosetQ, posets represent locations of values in a Young tableau:
| In[6]:= |
| Out[7]= |  |
Here are the corresponding posets:
| In[8]:= |
| Out[9]= | 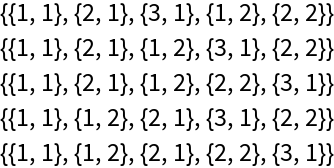 |
Happily, they are identified as posets:
| In[10]:= |
| Out[10]= |
Discounting n! problems, PosetQ can be used to find posets:
| In[11]:= |
| Out[11]= | 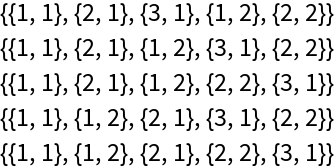 |
This function does not work with the posets used in HasseDiagram:
| In[12]:= |
| Out[12]= |
This is a valid partial ordering, but it is not coordinate based:
| In[13]:= |
| Out[13]= | 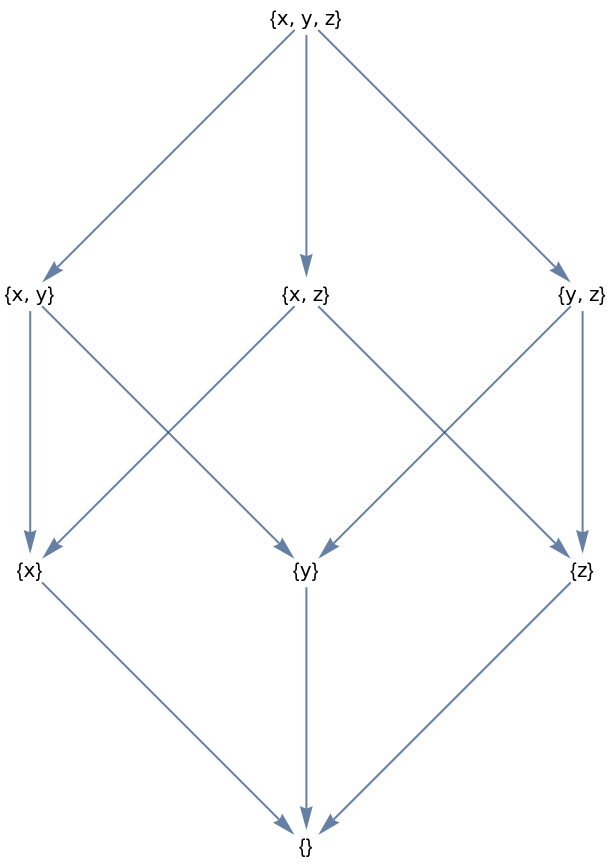 |
This work is licensed under a Creative Commons Attribution 4.0 International License