Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the Popov decomposition of a matrix of univariate polynomials
ResourceFunction["PopovDecomposition"][mat] computes the Popov decomposition of the matrix mat consisting of univariate polynomials. | |
ResourceFunction["PopovDecomposition"][mat,x] gives the Popov decomposition of the matrix mat regarded as univariate polynomials in the variable x. |
Compute the Popov decomposition for a 3×3 matrix of quartic polynomials:
| In[1]:= | ![{u, pop} = ResourceFunction[
"PopovDecomposition"][{{-8 + 5 x - 3 x^2 - 8 x^3 - 4 x^4, 2 + 4 x + 2 x^2 - 2 x^3 + 7 x^4, -1 - 10 x + 9 x^2 - 6 x^3 - 3 x^4}, {-2 + 5 x - 2 x^2 + 4 x^3 + 6 x^4, 4 + 5 x^2 - 8 x^3 - 5 x^4, 4 + 5 x - 3 x^2 - 6 x^3 - 6 x^4}, {-7 - 9 x + 8 x^2 + 9 x^3 + 2 x^4, 10 + x + 5 x^2 + 8 x^3 - 8 x^4, 4 + 5 x - 2 x^2 + x^3 - 9 x^4}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c6b/c6b83b72-0f96-4fe4-89a8-ac81b2a415c0/14785367fa80a7c5.png) |
| Out[1]= | 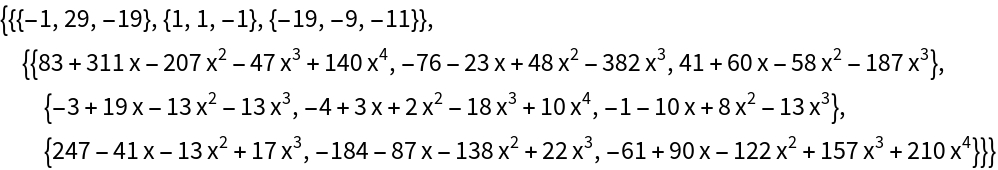 |
Check that the determinant is a constant:
| In[2]:= |
| Out[2]= |
Check that the necessary matrix identity is satisfied:
| In[3]:= |
| Out[3]= |
Check that the maximal degrees in each row move successively to the right:
| In[4]:= |
| Out[4]= |
Create a tool to generate a 3×3 matrix of quartic polynomials:
| In[5]:= |
If the input matrix does not have full row rank, there will be zero rows at the bottom of the Popov form (as many as the row rank deficiency):
| In[6]:= | ![SeedRandom[1111];
mat = randomMatrix[3, 2, 4, 10, x];
{u, pop} = ResourceFunction["PopovDecomposition"][mat]](https://www.wolframcloud.com/obj/resourcesystem/images/c6b/c6b83b72-0f96-4fe4-89a8-ac81b2a415c0/7e1cf93e794b58b7.png) |
| Out[3]= |  |
Generate a 3×3 matrix of quartic polynomials:
| In[7]:= | ![randomPoly[deg_, max_, x_] := RandomInteger[{-max, max}, deg + 1] . x^Range[0, deg]
randomMatrix[m_, n_, deg_, max_, x_] := Table[randomPoly[deg, max, x], {m}, {n}]
SeedRandom[1111];
mat = randomMatrix[3, 3, 4, 10, x];](https://www.wolframcloud.com/obj/resourcesystem/images/c6b/c6b83b72-0f96-4fe4-89a8-ac81b2a415c0/4c76656dd12be370.png) |
Compute the Popov decomposition over the integers modulo a prime:
| In[8]:= |
| Out[8]= | 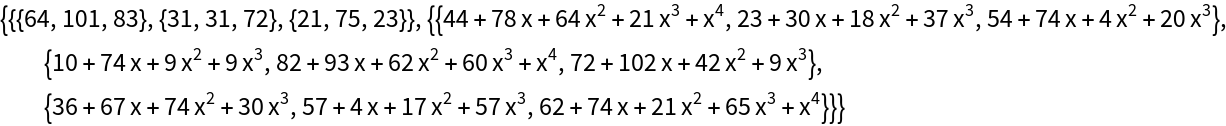 |
Check the necessary matrix identity:
| In[9]:= |
| Out[9]= |
This work is licensed under a Creative Commons Attribution 4.0 International License