Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the pooled variance of multiple lists of data
ResourceFunction["PooledVariance"][{l1,l2,…}] computes a weighted sum of the variances of each list li in which the weights are proportionate to the lengths of the constituent lists minus one. |
Compute the pooled variance of two lists of data, one of which has three values and variance of 4, and the other of which has four values and a variance of 15:
| In[1]:= |
| Out[1]= |
Compute the pooled variance of symbolic data, assuming that the elements of the data are real:
| In[2]:= |
| Out[2]= | 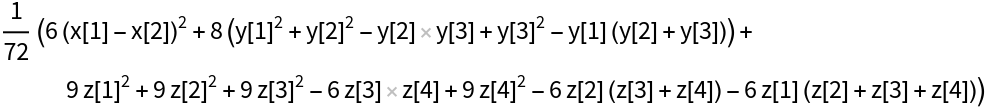 |
PooledVariance can work on collections of any finite length:
| In[3]:= |
| Out[3]= |
PooledVariance can work on complex values:
| In[4]:= |
| Out[4]= |
PooledVariance can work on symbolic values:
| In[5]:= |
| Out[5]= | 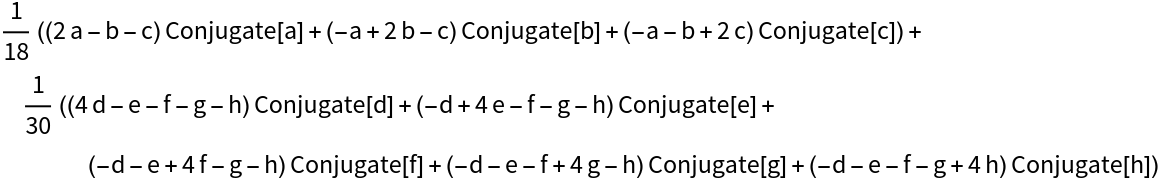 |
Compute Hedge’s g statistic, which makes use of the square root of a pooled variance to measure the effect size for the difference between means:
| In[6]:= | ![With[{data = {{2, 4, 6}, {3, 6, 9, 12}}}, Abs[{1, -1} . Mean /@ data/
Sqrt[ResourceFunction["PooledVariance"][data]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/ccf/ccf31a73-ecdf-4c85-858d-141245d6ff2c/09c4f48c2e93a4a2.png) |
| Out[6]= |
One can compute the pooled standard deviation by taking the square root of the pooled variance:
| In[7]:= |
| Out[7]= |
The same value can also be computed using the resource function PooledStandardDeviation:
| In[8]:= |
| Out[8]= |
The pooled variance of a collection is not the same as the variance of the flattened collection, even if the lengths of all the elements of the collection are the same:
| In[9]:= |
| Out[9]= |
PooledVariance will not evaluate unless each inner list has a length greater than 1:
| In[10]:= |
| Out[10]= |
This work is licensed under a Creative Commons Attribution 4.0 International License