Basic Examples (2)
Find an infeasibility certificate for the real system x2+y2=1 ∧ x4+y4≤1/4:
Verify that the matrices qi are positive semidefinite:
Verify the condition 1+∑i=1rsiγi==u1f1+…+ukfk:
Find an infeasibility certificate for the complex system x4+y4+z4=1 ∧ 2 x2 y2+z4=1 ∧ x≠y ∧ x≠-y:
Verify the condition u1f1+…+ukfk==g1e1·…·gmem:
We obtain a similar result by creating a new equation that forces both inequations to be False and removing the inequations:
Scope (6)
Infeasibility certificate for a real system of equations:
Verify correctness of the certificate:
Visualize the disjoint solution surfaces of the equations:
Infeasibility certificate for a real system of inequalities:
Verify correctness of the certificate:
Visualize the disjoint solution regions of the inequalities:
Infeasibility certificate for a real system of equations and inequalities:
Verify correctness of the certificate:
Visualize the disjoint solution sets of the equation and of the inequalities:
Find an infeasibility certificate for the complex system of equations:
Verify correctness of the certificate:
Find an infeasibility certificate for the complex system of equations and inequations:
Verify correctness of the certificate:
PolynomialSystemInfeasibilityCertificate returns unevaluated when it fails to find an infeasibility certificate:
In this case the system has solutions:
Applications (3)
Find an independently verifiable proof that surfaces x2+y2+z2=1 and x4+y4+z4=1/4 are disjoint:
Verify the proof:
Visualize the surfaces:
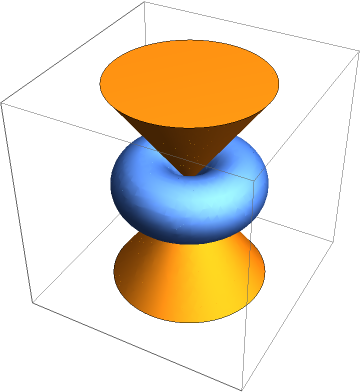
Find a proof that solids z2≥2 x2+2 y2 and 16 (x2+y2)≥(x2+y2+z2+2)2 are disjoint:
Verify the proof:
Visualize the solids:
Find a proof that x+y+z belongs to the radical of ⟨x3+y3+z3,(x+y)2 (x+z)2 (y+z)2⟩:
Verify that (x+y+z)e==u(x3+y3+z3)+v((x+y)2 (x+z)2 (y+z)2):
Properties and Relations (4)
PolynomialSystemInfeasibilityCertificate finds an independently verifiable certificate of infeasibility:
Verify correctness of the certificate:
FindInstance usually faster proves infeasibility, but does not provide a certificate:
You can also prove infeasibility using Resolve:
Possible Issues (3)
PolynomialSystemInfeasibilityCertificate may fail even if the problem is infeasible:
This shows that x2+y2-1=0∧-x3+2 y3-2-ε>=0 is infeasible for any ε>0:
For a larger value of ε PolynomialSystemInfeasibilityCertificate succeeds:
![ff = {x^2 + y^2 - 1};
gg = {1/4 - x^4 - y^4};
{tt, uu} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y}, Reals]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/0594af4869b1401d.png)

![ss = #[[2]] . #[[1]] . #[[2]] & /@ tt;
h = 1 + ss . ((Times @@ Part[gg, #[[3]]]) & /@ tt);
Expand[h - uu . ff]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/7e585f79843f8458.png)
![ff = {x^4 + y^4 + z^4 - 1, 2 x^2 y^2 + z^4 - 1};
gg = {x - y, x + y};
{uu, ee} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y, z}, Complexes]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/6f035eeb48c25501.png)
![ff = {x^2 + y^2 + z, z - 1};
gg = {};
{tt, uu} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y, z}, Reals];](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/0943cb391d206e02.png)
![ss = #[[2]] . #[[1]] . #[[2]] & /@ tt;
h = 1 + ss . ((Times @@ Part[gg, #[[3]]]) & /@ tt);
Expand[h - uu . ff]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/1a180bf068932e40.png)
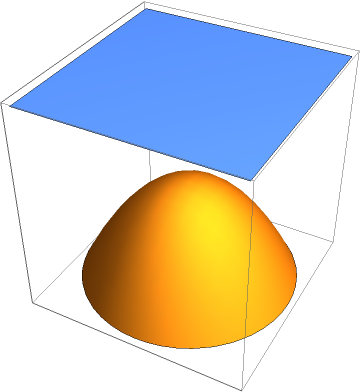
![ff = {};
gg = {1 - x^2 - y^2 - z^2, 1 - (x - 2)^4 - (y - 2)^4 - z^4};
{tt, uu} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y, z}, Reals];](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/5da8baabbde346f3.png)
![ss = #[[2]] . #[[1]] . #[[2]] & /@ tt;
h = 1 + ss . ((Times @@ Part[gg, #[[3]]]) & /@ tt);
Expand[h - uu . ff]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/1723fc5a0f476bcf.png)
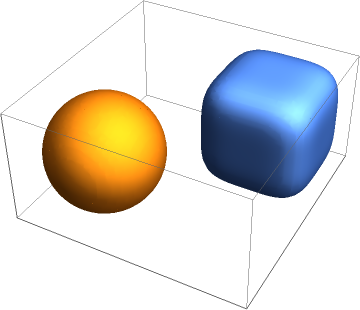
![ff = {x^2 + y^2 + z^2 - 1};
gg = {z^2 - 1/2, x^2 + y^2 - 2/3};
{tt, uu} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y, z}, Reals];](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/0b866a531a696a5a.png)
![ss = #[[2]] . #[[1]] . #[[2]] & /@ tt;
h = 1 + ss . ((Times @@ Part[gg, #[[3]]]) & /@ tt);
Expand[h - uu . ff]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/01105b6c79067682.png)
![Show[{ContourPlot3D[x^2 + y^2 + z^2 - 1 == 0, Sequence[{x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Ticks -> None, Mesh -> None]], RegionPlot3D[z^2 - 1/2 >= 0 && x^2 + y^2 - 2/3 >= 0, Sequence[{x, -1, 1}, {y, -1, 1}, {z, -1, 1}, PlotStyle -> Red, Ticks -> None, Mesh -> None]]}, ImageSize -> Small]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/33b108e679430343.png)

![ff = {x^2 - y, y^2 - z, x^4 - z + 1};
gg = {};
{uu, ee} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y, z}, Complexes]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/27f16202501b6438.png)
![ff = {(x^2 - y)^2, (y^2 - z)^3};
gg = {x^4 - z};
{uu, ee} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y, z}, Complexes]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/6ec5af584be229b4.png)
![ff = {x^2 + y^2 + z^2 - 1, x^4 + y^4 + z^4 - 1/4};
gg = {};
{tt, uu} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y, z}, Reals];](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/499011ca47d35e00.png)
![ss = #[[2]] . #[[1]] . #[[2]] & /@ tt;
h = 1 + ss . ((Times @@ Part[gg, #[[3]]]) & /@ tt);
Expand[h - uu . ff]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/1a6e9780c2c3e444.png)

![ff = {};
gg = {z^2 - 2 x^2 - 2 y^2, 16 (x^2 + y^2) - (x^2 + y^2 + z^2 + 2)^2};
{tt, uu} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y, z}, Reals];](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/5a82af0402294b01.png)
![ss = #[[2]] . #[[1]] . #[[2]] & /@ tt;
h = 1 + ss . ((Times @@ Part[gg, #[[3]]]) & /@ tt);
Expand[h - uu . ff]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/27a676a0a5edff2b.png)
![ff = {x^3 + y^3 + z^3, (x + y)^2 (x + z)^2 (y + z)^2};
g = x + y + z;
{{u, v}, {e}} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][
ff, {g}, {x, y, z}, Complexes]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/440ca87136a21527.png)
![ff = {x^8 + y^8 + z^8 - 1};
gg = {x^2 + y^2 - z^2, z - 99/100};
({tt, uu} = ResourceFunction["PolynomialSystemInfeasibilityCertificate"][ff, gg, {x, y, z}, Reals];) // AbsoluteTiming](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/68ee5c13e1d19336.png)
![ss = #[[2]] . #[[1]] . #[[2]] & /@ tt;
h = 1 + ss . ((Times @@ Part[gg, #[[3]]]) & /@ tt);
Expand[h - uu . ff]](https://www.wolframcloud.com/obj/resourcesystem/images/180/180da867-e35b-4237-bfb4-c0cfb47883ee/14160264a459b1e5.png)