Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PolynomialApproximation

Source Notebook

Approximate a function with a polynomial

Contributed by: Sander Huisman

ResourceFunction["PolynomialApproximation"][f,{x,xmin,xmax},n, "type"]

finds an nth order polynomial of a given type that approximates the function f for x∈[xmin,xmax].

Details

Supported values of "type" include:
"Taylor"Taylor expansion around (xmin+xmax)/2
"Equispaced"Polynomial going through n+1 points equispaced between xmin and xmax
"Chebyshev"Polynomial going through n+1 Chebyshev nodes
"Remez"Iteratively optimize the nodes starting with Chebyshev nodes
{“Remez”, m}Remez with m iterations

Examples

Basic Examples (5) 

Find the second-order Taylor polynomial approximating the sine function:

In[1]:=
ResourceFunction["PolynomialApproximation"][ Sin[x], {x, 0.0, Pi/2}, 2, "Taylor"]
Out[1]=

Compare with the original function:

In[2]:=
Plot[Sin[x] - %, {x, 0, Pi/2}]
Out[2]=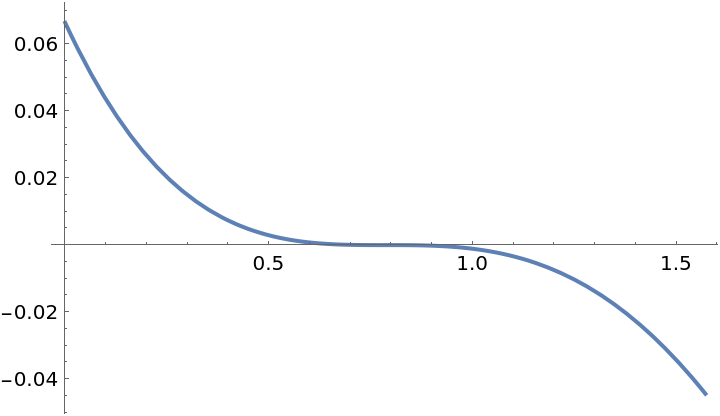

Use equispaced points to get a better approximation:

In[3]:=
f = Sin[x]; g = ResourceFunction["PolynomialApproximation"][f, {x, 0.0, Pi/2}, 2, "Equispaced"]; Plot[f - g, {x, 0, Pi/2}]
Out[5]=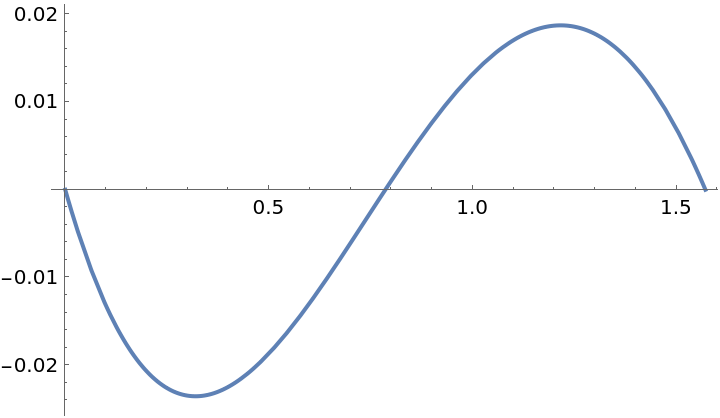

Use Chebyshev points to get an even better approximation:

In[6]:=
f = Sin[x]; g = ResourceFunction["PolynomialApproximation"][f, {x, 0.0, Pi/2}, 2, "Chebyshev"]; Plot[f - g, {x, 0, Pi/2}]
Out[8]=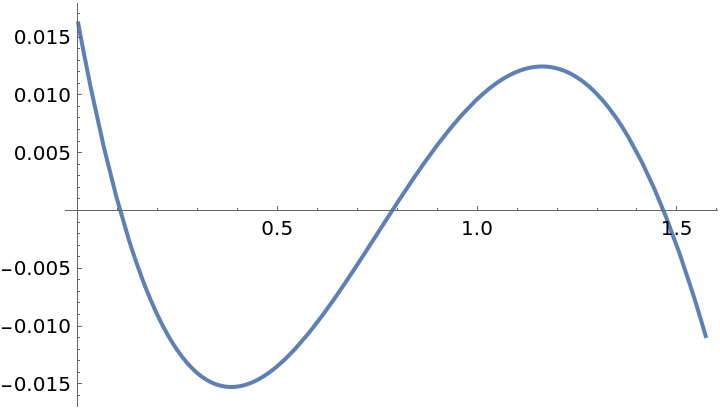

The polynomial produced by the Remez method yields a nearly-optimal approximation:

In[9]:=
f = Sin[x]; g = ResourceFunction["PolynomialApproximation"][f, {x, 0.0, Pi/2}, 2, "Remez"]; Plot[f - g, {x, 0, Pi/2}]
Out[11]=

Scope (1) 

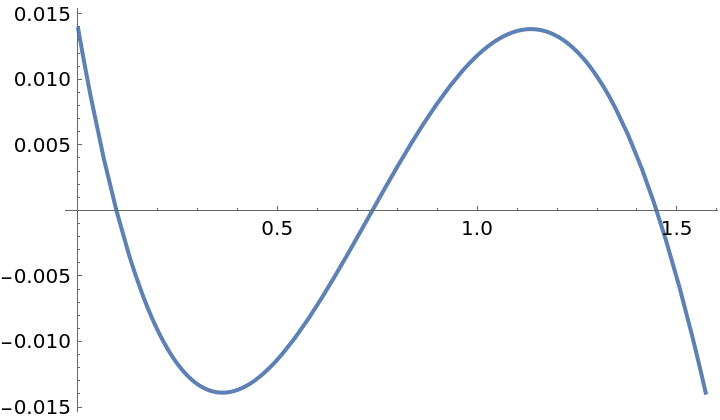Perform 6 iterations for the Remez method, and then compare the error:

In[12]:=
f = BesselJ[0, x]; g = ResourceFunction["PolynomialApproximation"][f, {x, 0.0, 3}, 5, {"Remez", 6}]; Plot[f - g, {x, 0, 3}]
Out[14]=

Applications (2) 

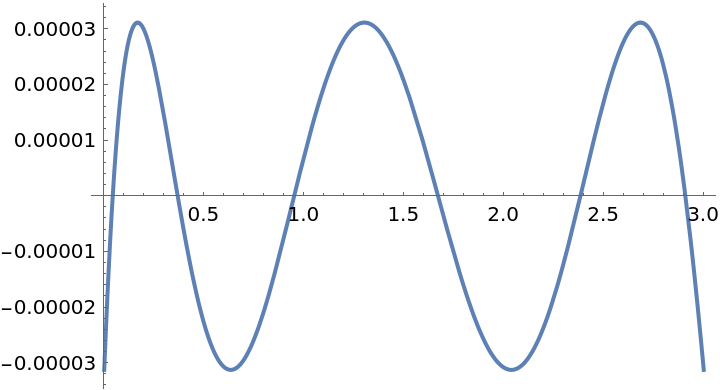Find a function that can approximate the cosine function for angles up to :

In[15]:=
f = Cos[x]; Plot[f, {x, 0, Pi/2}]
Out[16]=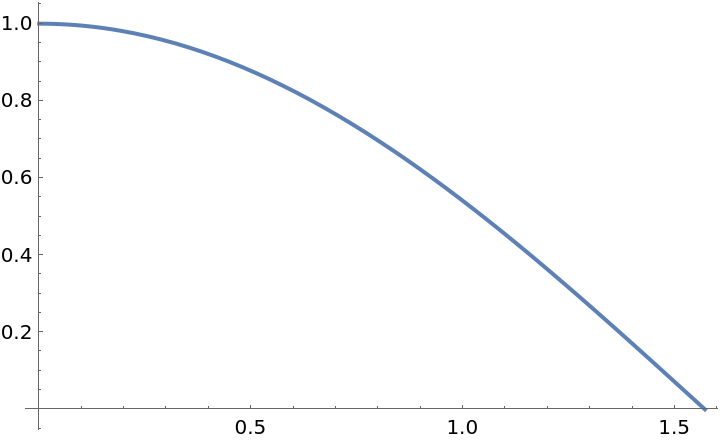

Calculate several orders and compare the maximum absolute error:

In[17]:=
gs = Table[ ResourceFunction["PolynomialApproximation"][f, {x, 0.0, Pi/2}, n, {"Remez", 8}] , {n, 2, 7} ]; LogPlot[Evaluate[Abs[(f - #)] & /@ gs], {x, 0, Pi/2}, PlotRange -> All, PlotLegends -> Range[2, 7], Frame -> True, PlotRangePadding -> {Scaled[.01], Scaled[.12]}, Axes -> False, PerformanceGoal -> "Speed"]
Out[18]=

Possible Issues (4) 

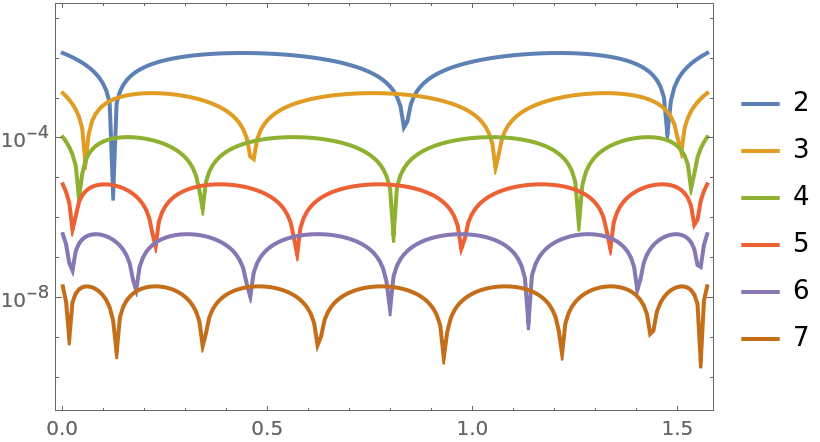The Remez method does not always converge:

In[19]:=
f = Cos[x]; g = ResourceFunction["PolynomialApproximation"][f, {x, 0.0, 3.0}, 3, {"Remez", 10}]; Plot[f - g, {x, 0, 3}]
Out[21]=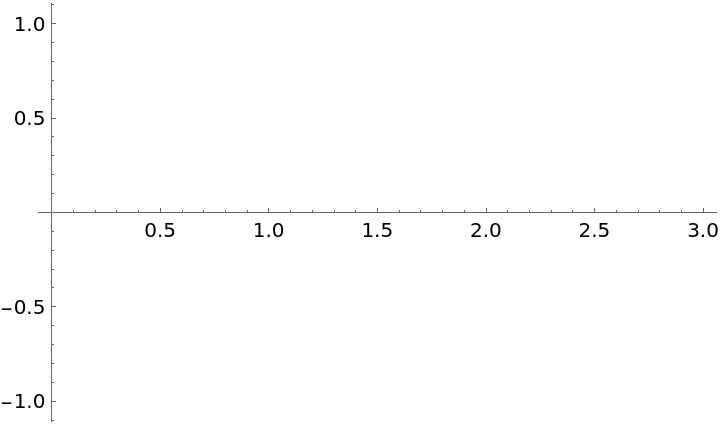

Higher order Remez might not converge to a good solution:

In[22]:=
f = Cos[x]; g = ResourceFunction["PolynomialApproximation"][f, {x, 0.0, 3}, 12, {"Remez", 20}]; Plot[f - g, {x, 0, 3}]
Out[24]=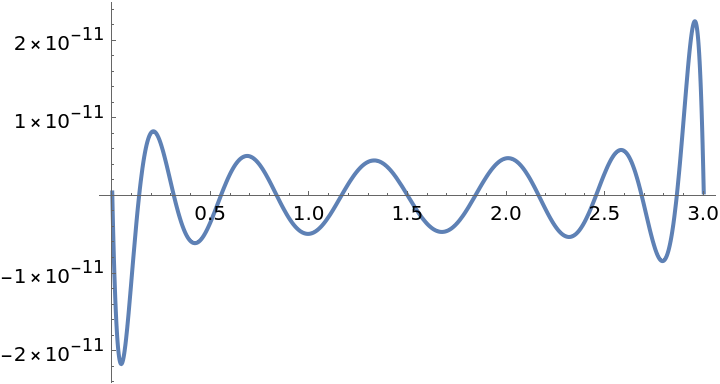

Higher order Remez might be prone to numerical errors:

In[25]:=
ResourceFunction["PolynomialApproximation"][ Cos[x], {x, 0.0, 3}, 16, "Remez"]
Out[25]=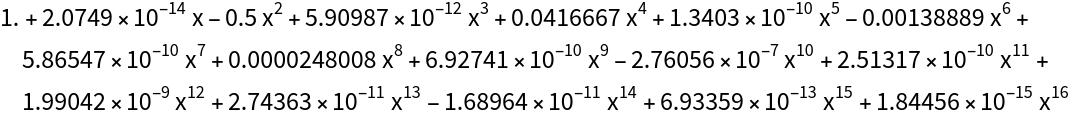

Functions that are not continuous can not be approximated very well:

In[26]:=
f = 1/(x - 1); g = ResourceFunction["PolynomialApproximation"][1/( x - 1), {x, 0.0, 3}, 5, "Equispaced"]; Plot[{f, g}, {x, 0, 3}]
Out[28]=

Neat Examples (3) 

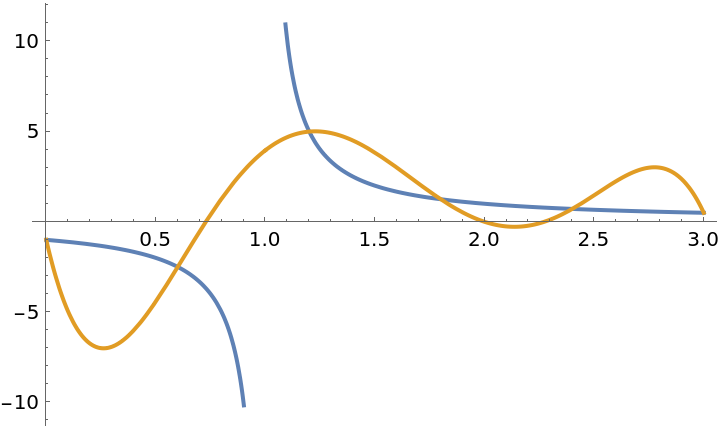Find a function that approximates a normal distribution:

In[29]:=
f = Exp[-x^2]; g = Quiet@ ResourceFunction["PolynomialApproximation"][f, {x, 0.0, 4}, 12, {"Remez", 8}]; Plot[f - g, {x, 0, 4}]
Out[31]=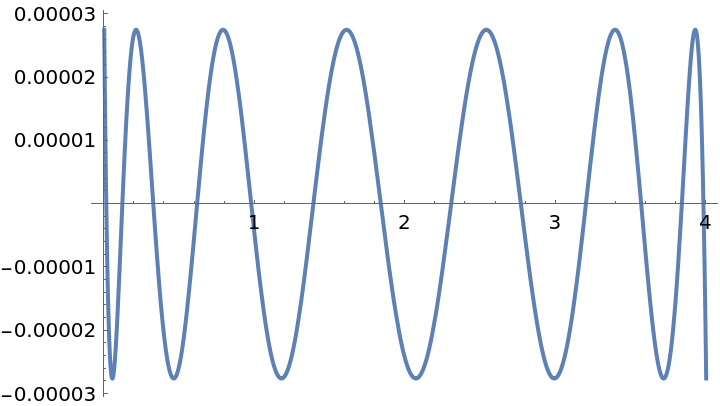

Find the maximum error:

In[32]:=
Quiet@Max[ First@FindMaximum[Abs[f - g], {x, #, 0, 4}] & /@ Subdivide[0, 4, 40]]
Out[32]=

Compare that to the Chebyshev case:

In[33]:=
f = Exp[-x^2]; g = Quiet@ ResourceFunction["PolynomialApproximation"][f, {x, 0.0, 4}, 12, "Chebyshev"]; Plot[f - g, {x, 0, 4}]
Out[34]=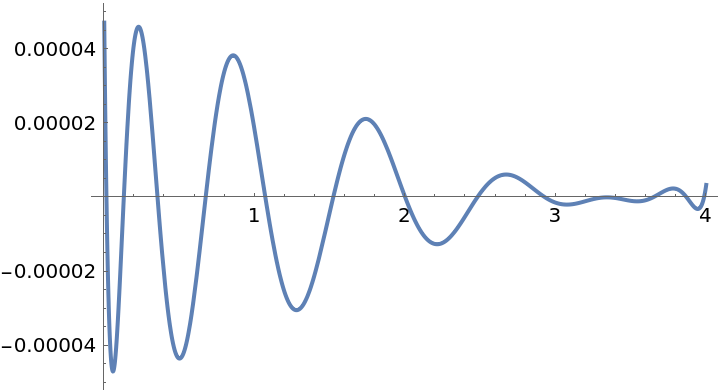
In[35]:=
Quiet@Max[ First@FindMaximum[Abs[f - g], {x, #, 0, 4}] & /@ Subdivide[0, 4, 40]]
Out[35]=

Publisher

SHuisman

Requirements

Wolfram Language 13.2 (December 2022) or above

Version History

  • 1.0.0 – 11 August 2023

Source Metadata

  • Citation:
    • Fraser W., "A Survey of Methods of Computing Minimax and Near-Minimax Polynomial Approximations for Functions of a Single Independent Variable." Journal of the ACM, vol. 12, no. 3, 295-314, 1965.
      DOI: 10.1145/321281.321282

Related Resources

Author Notes

Remez can be a bit 'unstable' as it numerically needs to find local maxima. I try to make sure these are unique, but can be hard to compare them considering numerical issues. Pade could be added using the existing function PadeApproximant, but can also be combined with Chebyshev points and Remez method for more complicated, more accurate approximations.

License Information