Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PolyhedronCanonicalForm

Source Notebook

Generate the canonical form of a convex polyhedron

Contributed by: Wolfram Staff (original content by George W. Hart)

ResourceFunction["PolyhedronCanonicalForm"][poly]

gives the canonical form of the convex polyhedron poly.

Details and Options

A convex polyhedron in canonical form is a polyhedron whose faces are all flat and whose edges are all tangent to the unit sphere centered at the origin, with the origin being the centroid of the points of tangency.
ResourceFunction["PolyhedronCanonicalForm"] accepts the following options:
MaxIterations100maximum number of iterations to use
ToleranceAutomatictolerance to be used for internal comparisons
WorkingPrecisionMachinePrecisionthe precision used in internal computations

Examples

Basic Examples (2) 

The tetrahedrally stellated icosahedron:

In[1]:=
tsi = Polyhedron[{{-1, GoldenRatio, 0}, {1, GoldenRatio, 0}, {-1, -GoldenRatio, 0}, {1, -GoldenRatio, 0}, {0, 1, -GoldenRatio}, {0, -1, -GoldenRatio}, {0, 1, GoldenRatio}, {0, -1, GoldenRatio}, {-GoldenRatio, 0, -1}, {-GoldenRatio, 0, 1}, {GoldenRatio, 0, -1}, {GoldenRatio, 0, 1}, {Rational[1, 5] (1 + 3 GoldenRatio), Rational[1, 5] (1 + 3 GoldenRatio), Rational[1, 5] (1 + 3 GoldenRatio)}, {Rational[1, 5] ( 1 + 3 GoldenRatio), Rational[1, 5] (-1 - 3 GoldenRatio), Rational[1, 5] (-1 - 3 GoldenRatio)}, {Rational[ 1, 5] (-1 - 3 GoldenRatio), Rational[1, 5] (1 + 3 GoldenRatio), Rational[1, 5] (-1 - 3 GoldenRatio)}, {Rational[ 1, 5] (-1 - 3 GoldenRatio), Rational[1, 5] (-1 - 3 GoldenRatio), Rational[1, 5] (1 + 3 GoldenRatio)}}, {{1, 2, 5, 15}, {1, 7, 13, 2}, {3, 4, 14, 6}, {3, 4, 8, 16}, {5, 6, 9, 15}, {5, 6, 14, 11}, {7, 8, 16, 10}, {7, 8, 12, 13}, {9, 10, 1, 15}, {9, 10, 16, 3}, {11, 12, 13, 2}, {11, 12, 4, 14}, {1, 7, 10}, {2, 5, 11}, {3, 6, 9}, {4, 8, 12}}];
In[2]:=
Graphics3D[tsi, Boxed -> False]
Out[2]=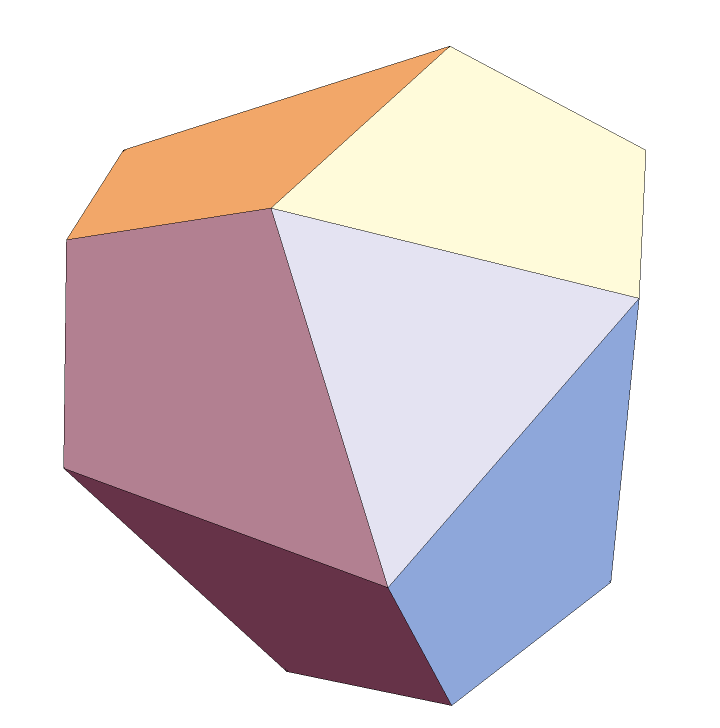

The canonical form of the polyhedron:

In[3]:=
cf = ResourceFunction["PolyhedronCanonicalForm"][tsi]
Out[3]=
In[4]:=
Graphics3D[cf, Boxed -> False]
Out[4]=

Scope (1) 

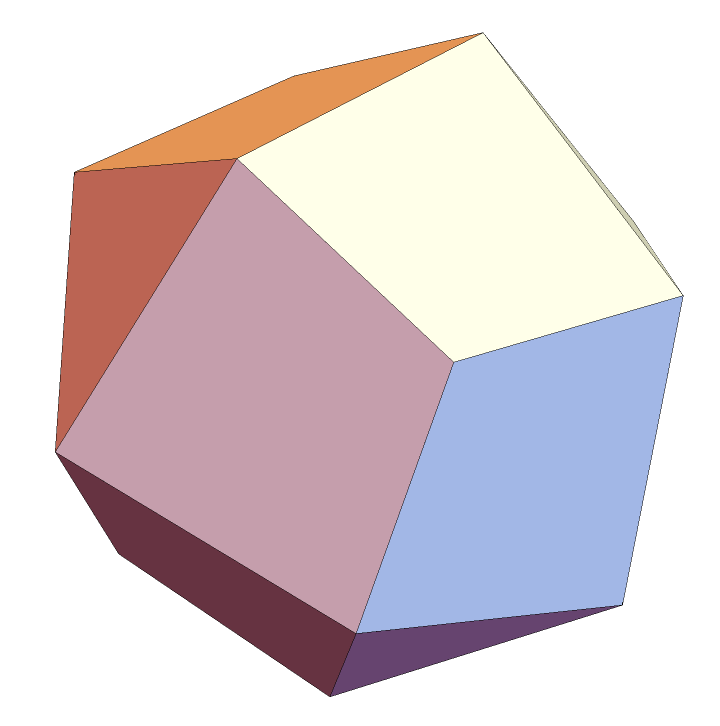PolyhedronCanonicalForm can be used on MeshRegion or BoundaryMeshRegion objects:

In[5]:=
ResourceFunction["PolyhedronCanonicalForm"][ PolyhedronData["Gyrobifastigium", "BoundaryMeshRegion"]]
Out[5]=

Options (3) 

MaxIterations (1) 

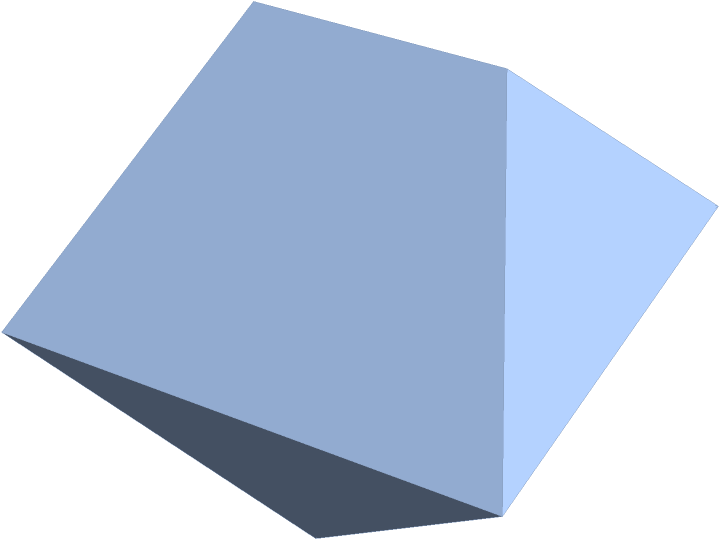Use a smaller number of iterations:

In[6]:=
ResourceFunction[ "PolyhedronCanonicalForm"][Polyhedron[{{-0.5, 0., 0.}, {0., -0.5, 1.5678618484651274`}, {0., 0.5, 1.5678618484651274`}, { 0., -0.644584273224155, 0.5783693583793041}, {0., 0.6445842732241549, 0.5783693583793041}, {0.5, 0., 0.}, {-0.644584273224155, 0., 0.9894924900858232}, { 0.6445842732241549, 0., 0.9894924900858232}}, {{2, 3, 7}, {3, 2, 8}, {4, 2, 7}, {2, 4, 8}, {6, 8, 4}, {4, 1, 6}, {7, 1, 4}, {3, 5, 7}, {8, 5, 3}, {5, 8, 6}, {5, 6, 1}, {5, 1, 7}}], MaxIterations -> 60]
Out[6]=

Tolerance (1) 

Use a looser tolerance:

In[7]:=
ResourceFunction[ "PolyhedronCanonicalForm"][Polyhedron[{{-0.5, 0., 0.}, {0., -0.5, 1.5678618484651274`}, {0., 0.5, 1.5678618484651274`}, { 0., -0.644584273224155, 0.5783693583793041}, {0., 0.6445842732241549, 0.5783693583793041}, {0.5, 0., 0.}, {-0.644584273224155, 0., 0.9894924900858232}, { 0.6445842732241549, 0., 0.9894924900858232}}, {{2, 3, 7}, {3, 2, 8}, {4, 2, 7}, {2, 4, 8}, {6, 8, 4}, {4, 1, 6}, {7, 1, 4}, {3, 5, 7}, {8, 5, 3}, {5, 8, 6}, {5, 6, 1}, {5, 1, 7}}], Tolerance -> 1.*^-5]
Out[7]=

WorkingPrecision (1) 

Use a higher precision setting in internal computations:

In[8]:=
ResourceFunction[ "PolyhedronCanonicalForm"][Polyhedron[{{-0.5, 0., 0.}, {0., -0.5, 1.5678618484651274`}, {0., 0.5, 1.5678618484651274`}, { 0., -0.644584273224155, 0.5783693583793041}, {0., 0.6445842732241549, 0.5783693583793041}, {0.5, 0., 0.}, {-0.644584273224155, 0., 0.9894924900858232}, { 0.6445842732241549, 0., 0.9894924900858232}}, {{2, 3, 7}, {3, 2, 8}, {4, 2, 7}, {2, 4, 8}, {6, 8, 4}, {4, 1, 6}, {7, 1, 4}, {3, 5, 7}, {8, 5, 3}, {5, 8, 6}, {5, 6, 1}, {5, 1, 7}}], WorkingPrecision -> 25]
Out[8]=

Applications (3) 

Define J. H. Conway's "hermaphrodite" polyhedron:

In[9]:=
conwayHermaphrodite[n_Integer] := Polyhedron[ Join[Table[{Cos[2 \[Pi] i/n], Sin[2 \[Pi] i/n], -1}, {i, n}], Table[{Cos[2 \[Pi] i/n], Sin[2 \[Pi] i/n], 0}, {i, n}], {{0, 0, 1}}], Join[{Range[n], {1, n + 1, 2 n, n}, {n + 1, 2 n, 2 n + 1}}, Table[{i, i + 1, n + i + 1, n + i}, {i, n - 1}], Table[{n + i, n + i + 1, 2 n + 1}, {i, n - 1}]]]
In[10]:=
Graphics3D[conwayHermaphrodite[7], Boxed -> False]
Out[10]=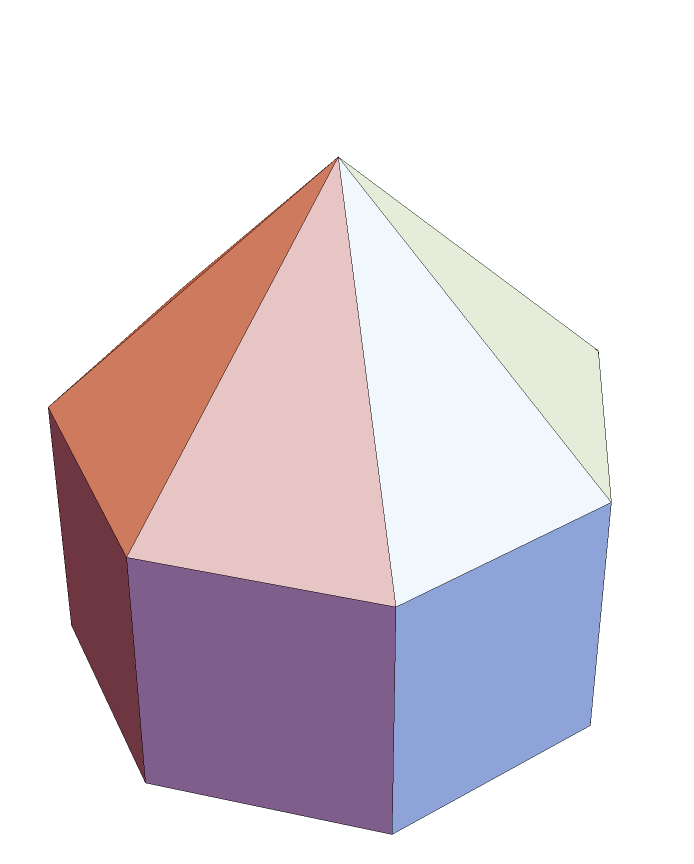

Visualize the canonical form:

In[11]:=
Graphics3D[ chcf = ResourceFunction["PolyhedronCanonicalForm"][ conwayHermaphrodite[7]], Boxed -> False]
Out[11]=

The canonical form is self-dual:

In[12]:=
Graphics3D[{{Blue, chcf}, {Yellow, GeometricTransformation[chcf, ScalingTransform[-{1, 1, 1}]]}}, Boxed -> False]
Out[12]=

Version History

  • 1.0.0 – 21 June 2021

Source Metadata

  • Citation:
    • Hart, G.W., "Calculating Canonical Polyhedra." Mathematica in Education and Research, vol. 6, no. 3, 5-10, 1997.

Related Resources

License Information