Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PolygonalDiagram

Source Notebook

Show an array of polygonal numbers

Contributed by: Wolfram Staff (original work by Eric W. Weisstein)

ResourceFunction["PolygonalDiagram"][n,m]

gives a regular polygon of n sides with m levels of numbers arranged in equally spaced points.

Details and Options

A polygonal number is an array of n successive natural numbers that can be arranged in a triangle, square, etc. for some values of n, depending on the sides of the polygon.
In general, any n-gonal number is equal to the sum of the (n-1)-gonal number of the same rank and the triangular number of the previous rank.
ResourceFunction["PolygonalDiagram"] accepts the same options as Graphics.

Examples

Basic Examples (1) 

Get a diagram with a triangle with four levels:

In[1]:=
ResourceFunction["PolygonalDiagram"][3, 4]
Out[1]=

Scope (2) 

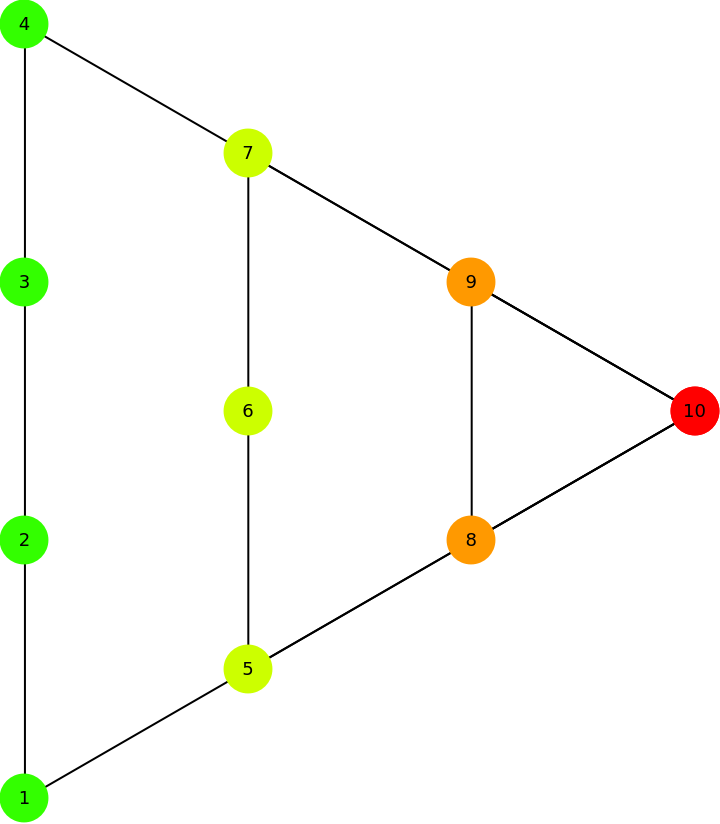
First five triangular numbers and their diagrams:

In[2]:=
Table[PolygonalNumber[n], {n, 5}]
Out[2]=
In[3]:=
GraphicsRow[Table[ResourceFunction["PolygonalDiagram"][3, k], {k, 5}], ImageSize -> {Automatic, 180}]
Out[3]=

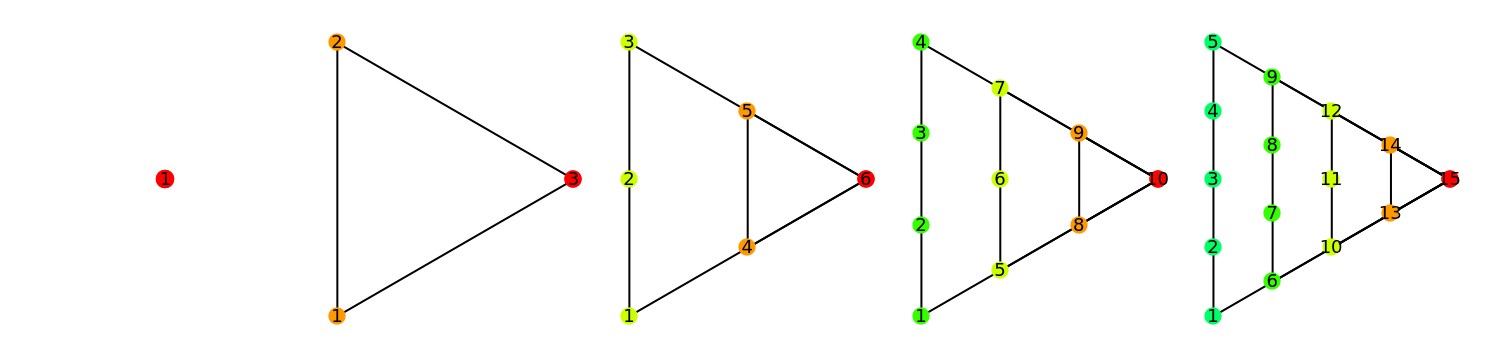
Four-level diagrams for various polygonal numbers:

In[4]:=
GraphicsRow[ Table[ResourceFunction["PolygonalDiagram"][j, 4], {j, 3, 7}], ImageSize -> {Automatic, 180}]
Out[4]=

Options (1) 

PlotLabel (1) 

Add a PlotLabel to the diagram:

In[5]:=
ResourceFunction["PolygonalDiagram"][3, 4, PlotLabel -> Automatic]
Out[5]=

Applications (1) 

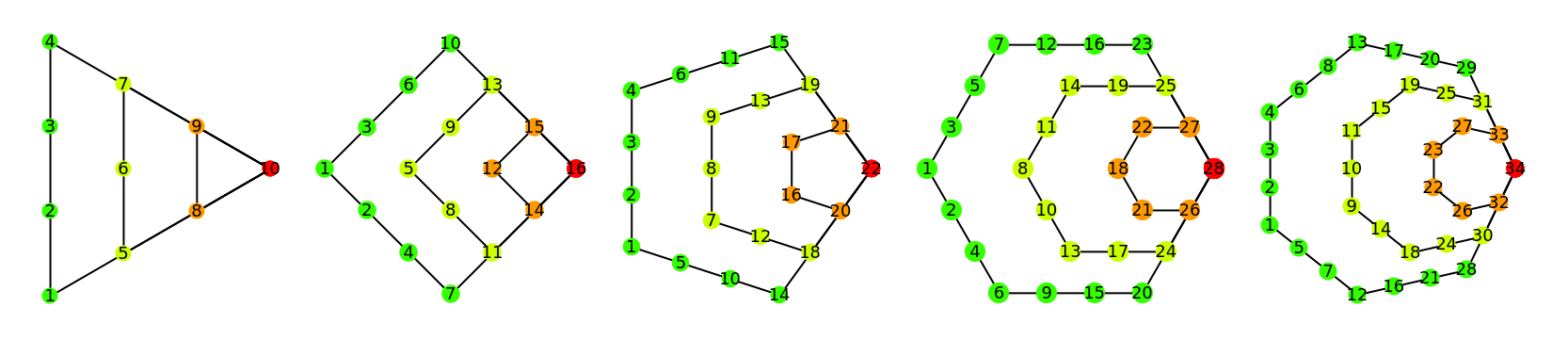
Demonstrate the addition of polygonal numbers:

In[6]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/54be2a52-c4d4-4438-9373-a80b9ab18094"]
Out[6]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 2.0.0 – 14 September 2021
  • 1.0.0 – 19 April 2019

License Information