Basic Examples (2) 

Compute an interpolation of vertex values at the center of a equilateral triangle:

In[1]:=

Out[1]=

Calculate the vertices of a pentagon:

In[2]:=

Out[2]=

Compute the value of a function at each vertex:

In[3]:=

In[4]:=

Out[4]=

Find the value of an interpolation of the values at a point within the polygon:

In[5]:=

Out[5]=

Scope (2) 

A triangle:

In[6]:=

Out[6]=

Define values at the triangle's vertices for a linear function:

In[7]:=

Out[7]=

Evaluate the interpolant at a single point:

In[8]:=

Out[8]=

Evaluate the interpolant at multiple points:

In[9]:=

Out[9]=

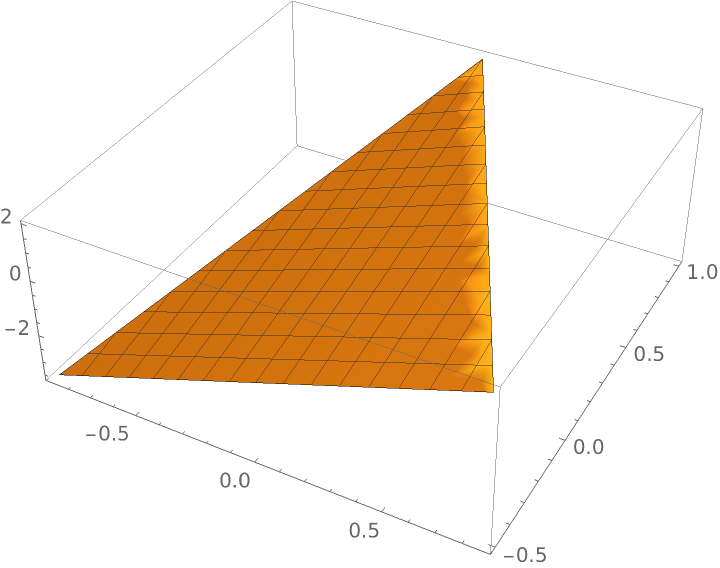
Plot the interpolant over the triangle:

In[10]:=

Out[10]=

A star-shaped Polygon:

In[11]:=

Values at the polygon's vertices:

In[12]:=

Evaluate the interpolant at a single point:

In[13]:=

Out[13]=

Evaluate the interpolant at multiple points:

In[14]:=

Out[14]=

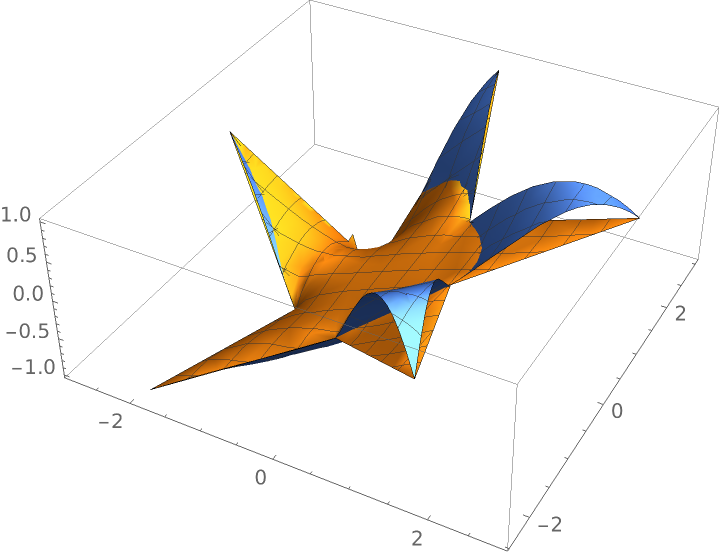
Plot the interpolant along with the original function over the star-shaped polygon:

In[15]:=

Out[15]=

Applications (3) 

Vertices for a bean-shaped polygon, and colors specified as RGB components:

In[16]:=

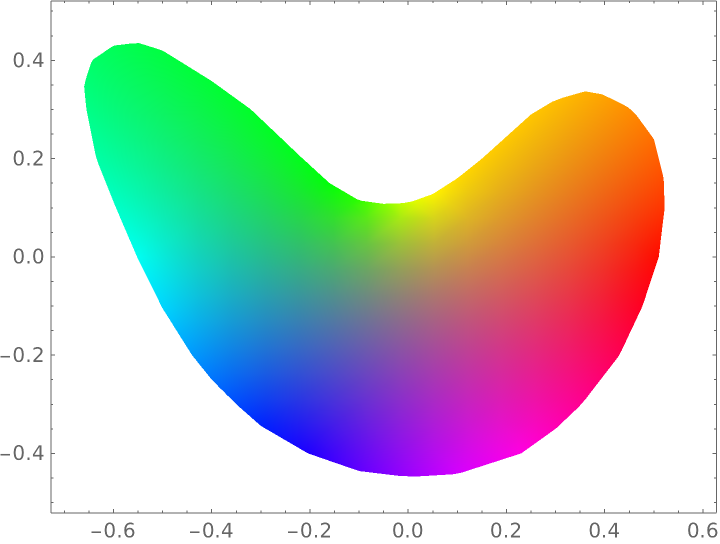
Visualize the polygon colored using PolygonInterpolation:

In[17]:=

Out[17]=

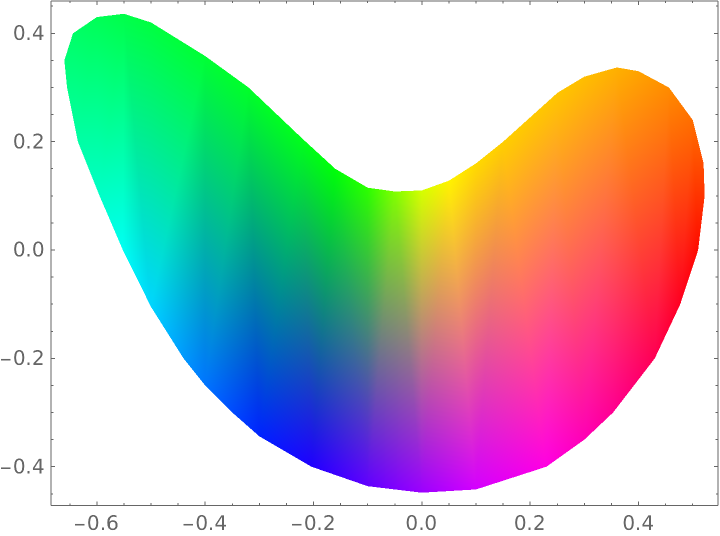
Compare with the result of using the VertexColors option of Polygon:

In[18]:=

Out[18]=

Neat Examples (4) 

Define a polygon using FindShortestTour over grid points:

In[19]:=

See the polygon:

In[20]:=

Out[20]=

Define an arbitrary function and map it over all the vertices:

In[21]:=

Out[21]=

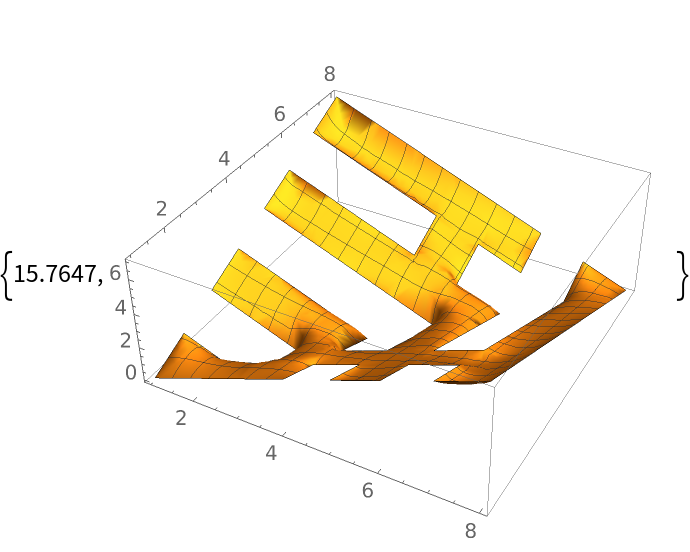
For 64 vertices, visualizing the results takes a few seconds:

In[22]:=

Out[22]=