Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PolygonFromBase

Source Notebook

Build a regular polygon on a given line segment

Contributed by: Ed Pegg Jr

ResourceFunction["PolygonFromBase"][base,n]

builds a regular n-gon on the line segment base.

Details

The polygon is constructed counterclockwise by keeping the interior to the left as one goes from initial to terminal point on the base segment.
Reversing the base reverses the orientation of the constructed polygon.

Examples

Basic Examples (2) 

Build an equilateral triangle on a base segment:

In[1]:=
base = {{0, 1}, {2, 3}}; poly = ResourceFunction["PolygonFromBase"][base, 3]
Out[2]=

Show the construction:

In[3]:=
Graphics[{Line[base], Green, Line[poly]}, ImageSize -> Small]
Out[3]=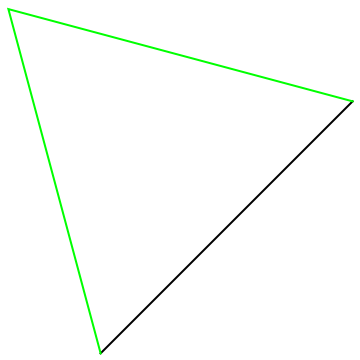

Build a series of polygons on a base:

In[4]:=
base = {{0, 0}, {1, 1}}; Graphics[{Line[base], Table[{Hue[n/13], Line[ResourceFunction["PolygonFromBase"][N[base], n]]}, {n, 3, 12}]}, ImageSize -> Small]
Out[5]=

Applications (1) 

Show the intersection giving the Fermat point:

In[6]:=
{x, y, z} = {{-0.18, -0.21}, {-0.53, -0.42}, {-0.38, 0.78}}; tris = ResourceFunction["PolygonFromBase"][#, 3] & /@ Partition[{x, y, z}, 2, 1, 1]; Graphics[{EdgeForm[Black], Green, Polygon[{x, y, z}], LightBlue, Polygon /@ tris, Red, Table[InfiniteLine[{{x, y, z}[[Mod[n + 2, 3, 1]]], tris[[n, 2]]}], {n, 1, 3}]}, ImageSize -> Small]
Out[7]=

Properties and Relations (1) 

Reversing the order of the points in the base segment gives a reflected polygon:

In[8]:=
n = 7; base = N@{{0, 1}, {2, 3}}; Graphics[{Line[base], {Green, Line[ResourceFunction["PolygonFromBase"][base, n]]}, {Blue, Line[ResourceFunction["PolygonFromBase"][Reverse[base], n]]}}, ImageSize -> Small]
Out[9]=

Neat Examples (2) 

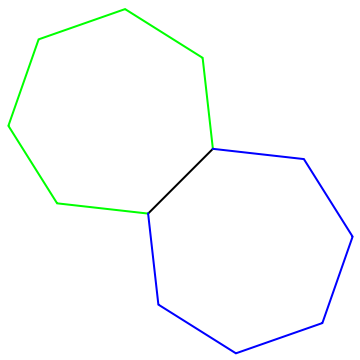Build a regular hexagon from an arbitrary triangle:

In[10]:=
{x, y, z} = RandomReal[{-1, 1}, {3, 2}]; g = Mean[{x, y, z}]; x1 = 2 x - g; x2 = 2 g - x1; y1 = 2 y - g; y2 = 2 g - y1; z1 = 2 z - g; z2 = 2 g - z1; tris = ResourceFunction["PolygonFromBase"][#, 3] & /@ Partition[{x1, y2, z1, x2, y1, z2}, 2, 1, 1]; Graphics[{EdgeForm[Black], Opacity[.4], White, Polygon[#[[2]] & /@ tris], Polygon[{x1, y2, z1, x2, y1, z2}], LightBlue, Polygon /@ tris, Polygon[{x, y, z}], Black, Line[{g, #}] & /@ {x1, y2, z1, x2, y1, z2}}]
Out[11]=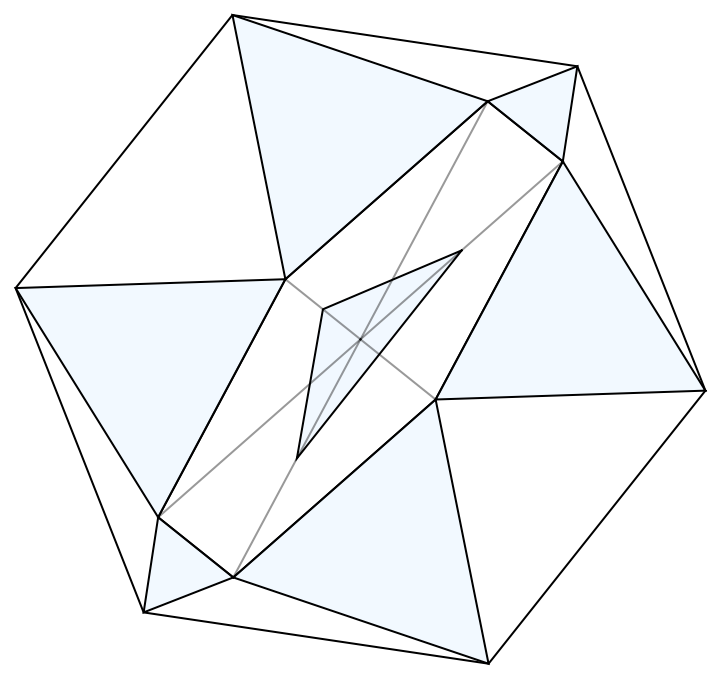

A polygonal random walk:

In[12]:=
n = 5; Graphics[ Map[{RandomColor[], Polygon[#]} &, NestList[ With[{base = #[[RandomInteger[{2, n - 2}] + {1, 0}]]}, ResourceFunction["PolygonFromBase"][base, n]] &, N[CirclePoints[n]], 20]]]
Out[45]=

Version History

  • 1.0.0 – 09 May 2022

Related Resources

Author Notes

Equivalent definitions include:

In[1]:=
PolygonFromBase[base_?MatrixQ, n_Integer] /; Dimensions[base] === {2, 2} && n > 2 := Module[{cen, diff, sideHalf}, diff = {-1, 1} . base; sideHalf = Norm[diff]/2; cen = RootReduce[ Mean[base] + sideHalf Cot[\[Pi]/n] Normalize[Cross[diff]]]; CirclePoints[ cen, {RootReduce[sideHalf Csc[\[Pi]/n]], Arg[diff . {1, I}] - (\[Pi] (n - 2))/(2 n)}, n]]
In[2]:=
PolygonFromBase[base_?MatrixQ, n_Integer] /; Dimensions[base] === {2, 2} && n > 2 := Module[{diff = {-1, 1} . base, cr}, cr = Cross[diff]; TranslationTransform[Mean[base] + 1/2 Cot[\[Pi]/n] cr][ CirclePoints[{1/2 Csc[\[Pi]/n], -\[Pi] (n - 2)/(2 n)}, n] . {diff, cr}]]

License Information