Basic Examples (2) 

Find the area of a 3D triangle:

In[1]:=

Out[1]=

Find the area of the faces of a tetrahedron:

In[2]:=

Out[2]=

Scope (3) 

Specify the polygon using Polygon:

In[3]:=

Out[3]=

Specify the polygon using Triangle:

In[4]:=

Out[4]=

Calculate the areas for faces of a dodecahedron:

In[5]:=

Out[7]=

Properties and Relations (2) 

Find the area of one face of the d120:

In[8]:=

Out[9]=

Measure the areas of all 120 faces with TriangleArea3D and get the time required:

In[10]:=

Out[10]=

Measure the areas of all 120 faces with RegionMeasure and get the time required:

In[11]:=

Out[11]=

Measure the areas of all 120 faces with the HeronFormula and get the time required:

In[12]:=

Out[12]=

Timings with exact values:

In[13]:=

Out[13]=

In[14]:=

Out[14]=

PolygonArea3D cannot find the area of a triangle with a variable:

In[15]:=

Out[15]=

RegionMeasure can find the area of a triangle with a variable:

In[16]:=

Out[16]=

Possible Issues (2) 

Point order matters. Find the area of a larger polygon:

In[17]:=

Out[18]=

Show the polygon:

In[19]:=

Out[19]=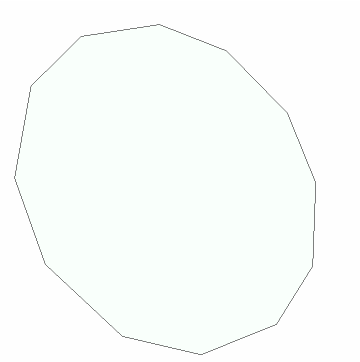

Calculate the area of the points in a different order:

In[20]:=

Out[21]=

Show the polygon:

In[22]:=

Out[22]=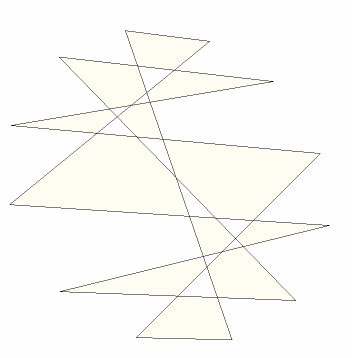

The following points are not planar:

In[23]:=

Out[24]=

Therefore, this computed area is spurious:

In[25]:=

Out[25]=