Basic Examples (1) 

Compute the polar decomposition for a 4×3 matrix:

In[1]:=

Out[1]=

Scope (2) 

Compute the polar decomposition of a complex matrix:

In[2]:=

Out[2]=

A matrix with entries having 20-digit precision:

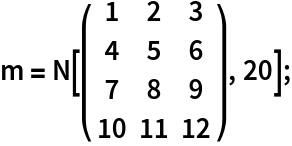
The polar decomposition is computed using the full 20-digit precision of the input:

In[3]:=

Out[3]=

Properties and Relations (2) 

A random 5×4 matrix m:

Compute its polar decomposition:

In[4]:=

Out[4]=

The columns of q are orthonormal:

In[5]:=

Out[5]=

The matrix s is Hermitian positive semidefinite:

In[6]:=

Out[6]=

The matrix s is equal to MatrixPower[ConjugateTranspose[m].m,1/2]:

In[7]:=

Out[7]=

m is equal to q.s:

In[8]:=

Out[8]=

If the matrix m is Hermitian positive semidefinite, then q is equal to the identity matrix, and s is equal to m:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

Possible Issues (1) 

PolarDecomposition only works with approximate numerical matrices:

In[11]:=

Out[11]=

In[12]:=

Out[12]=