Details and Options
A finite object with a well-defined shape is often symmetrical, that is, it can be reoriented and superimposed upon itself. The most familiar symmetrical objects are polygons and polyhedra. For example, a square can be turned in increments of 90° and look as though it had not been moved. In 3-dimensional space there are three kinds of operations that can bring an object into coincidence with itself: a rotation about an axis, a reflection across a plane, and a rotary-reflection (rotation about an axis followed by reflection across a plane perpendicular to the axis; inversion through a point is a special case of this kind of operation). When more than one operation exists for an object, they can be combined in pairs to generate new operations. However, there is generally only a finite number of these combinations, and mathematically they have the structure of a group. Geometrically, they all intersect at a point or along a line. Hence the name "symmetry point group" for the collection of operations. While ancient philosophers, such as Plato, recognized these symmetries, it wasn't until the end of the 19th century that crystallographers codified the naming of these point groups. There are a number of naming conventions in use today by mathematicians, chemists, and physicists. The two most common are the Schoenflies and the Hermann-Mauguin symmetry point group symbols. The latter is also known as the International symmetry point group symbol, as it is used in the International Tables for Crystallography.
The finite symmetry point groups can be placed into five classes: axial, dihedral, tetrahedral, octahedral, and icosahedral. The first two have a principal n-fold rotation axis, and the latter three have multiple, intersecting threefold, fourfold, and fivefold rotation axes, respectively. In the Schoenflies system, the axial groups are given the symbol C or S, the dihedral groups the symbol D, the tetrahedral groups the symbol T, the octahedral groups the symbol O, and the icosahedral groups the symbol I. For the cyclic and dihedral groups, the order of the rotation axis (that is, the number of partial turns, n, that produce a complete cycle) is given as a subscript. For example, the cyclic group with a threefold rotation axis is given the symbol C3. If the principal axis of the cyclic group is a rotary-reflection (also known as an improper rotation) axis, then the symbol S is given. The order of rotary-reflection axes is always even, e.g., S4. If mirror planes parallel to the principal axis are present, the subscript v is added (for “vertical”); e.g., C3v. If instead a mirror plane perpendicular to the principal axis is present, the subscript h is added (for “horizontal”); e.g., C3h. The dihedral groups are similar to the cyclic groups, but additionally have twofold rotation axes perpendicular to the principal axis. If mirror planes parallel to the principal axis are present the subscript d is used (for “diagonal”); e.g., D3d.
There are three so-called non-axial symmetry point groups. The group Cs has just a mirror plane, and is the same as C1v and C1h. The group Ci has just a center of inversion, and is the same as S2. The group C1 has no symmetry elements.
The tetrahedral symmetry group has 3 mutually perpendicular twofold rotation axes and four threefold rotation axes that meet at an angle of arc cos -
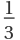
, or approximately 109.47°, and is given the symbol
T. If additionally a center of inversion is present, the subscript
h is added, e.g.,
Th. If instead there are mirror planes parallel with the threefold rotation axes, the subscript d is added, e.g.,
Td. The octahedral group is given the symbol
O, and has three mutually perpendicular fourfold rotation axes, four threefold rotation axes meeting at an angle of arc cos -
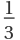
, six twofold rotation axes. If mirror planes and a center of inversion are present the subscript h is added, e.g.,
Oh. The icosahedral group has six fivefold rotation axes, ten 3-threefold rotation axes, and fifteen twofold rotation axes, and is given the symbol
I. If mirror planes and a center of inversion are present, then the subscript
h is added, e.g.,
Ih.
There are three infinite symmetry point groups relevant to the structure of molecules, and they possess a principal ∞-fold rotation axis. The cyclic infinite point group also has mirror planes parallel to the principal rotation axis and is given the symbol C{XMLElement[span, {class -> stylebox}, {∞, XMLElement[i, {class -> ti}, {v}]}]}. The dihedral infinite point group also has a mirror plane perpendicular to the principal rotation axis and is given the symbol D{XMLElement[span, {class -> stylebox}, {∞, XMLElement[i, {class -> ti}, {h}]}]}. The third infinite symmetry point group is that for a perfect sphere. It has an infinite number of ∞-fold rotation axes and an infinite number of mirror planes, and is given the symbol Kh (for "Kugel").
The output is a
Subscript object, and is from one of the following symmetry point group families:
| Cn | cyclic; n-fold rotation axis |
| Cnv | cyclic; n-fold rotation axis with mirror planes parallel to rotation axis; C1v=Cs |
| Cnh | cyclic; n-fold rotation axis with mirror plane perpendicular to rotation axis; C1h=Cs |
| S2n | cyclic; 2n-fold rotary-reflection axis; S2=Ci |
| Dn | dihedral; n-fold princicpal rotation axis and twofold rotation axes perpendicular to principal axis |
| Dnd | dihedral; n-fold princicpal rotation axis and twofold rotation axes perpendicular to principal axis with mirror planes parallel to principal axis |
| Dnh | dihedral; n-fold princicpal rotation axis and twofold rotation axes perpendicular to principal axis with mirror planes parallel to principal axis and a mirror plane perpendicular to principal axis |
| T | tetrahedral; four threefold rotation axes and three twofold rotation axes |
| Th | tetrahedral; four threefold rotation axes and three twofold rotation axes with center of inversion |
| Td | tetrahedral; four threefold rotation axes and three twofold rotation axes with mirror planes |
| O | octahedral; three 4-fold rotation axes, four threefold rotation axes, and six twofold rotation axes |
| Oh | octahedral; three 4-fold rotation axes, four threefold rotation axes, and six twofold rotation axes with center of inversion |
| I | icosahedral; six fivefold rotation axes, ten threefold rotation axes, and fifteen twofold rotation axes |
| Ih | icosahedral; six fivefold rotation axes, ten threefold rotation axes, and fifteen twofold rotation axes with center of inversion |
| C{XMLElement[span, {class -> stylebox}, {∞, XMLElement[i, {class -> ti}, {v}]}]} | continuous, linear; ∞-fold principal rotation axis with mirror planes parallel to principal axis |
| D{XMLElement[span, {class -> stylebox}, {∞, XMLElement[i, {class -> ti}, {h}]}]} | continuous, linear; ∞-fold principal rotation axis and ∞ twofold rotation axes perpendicular to principal axis with mirror planes parallel to rotation axis and a mirror plane perpendicular to the principal axis |
| Kh | continuous, spherical |
The following options can be given:
| "ComputeAtomCoordinates" | False | whether to compute atom coordinates if not present |
| "SymbolType" | "Schoenflies" | type of symbol to return; other choices are "HermannMauguin" and "International" |
| Tolerance | 0.0001 | the tolerance to use for internal comparisons |
The option "ComputeAtomCoordinates" may be used to specify the coordinates to be used. Available choices are:
It is the responsibility of the user to provide atom coordinates with the desired geometry, and thus the point symmetry. Most molecules can adopt many different shapes, and the distance geometry method used by
MoleculeModify can be somewhat arbitrary when the opportunity arises. Therefore the default setting is not
Automatic. It may be useful in some settings to include
SetOptions[ResourceFunction["PointGroupSymbol"],"ComputeAtomCoordinates"→Automatic] at the beginning of one’s notebook.
![ResourceFunction["PointGroupSymbol"][Molecule[{"H", "H"}, {
Bond[{1, 2}, "Single"]}, {}], "ComputeAtomCoordinates" -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/099b25072deb696c.png)
![ResourceFunction["PointGroupSymbol"][Molecule[{"F", "H"}, {
Bond[{1, 2}, "Single"]}, {}], "ComputeAtomCoordinates" -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/5bae6355aa185c18.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/5d4ee05a-7bd3-405f-b508-16fd421e5da3"]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/38c8c5660ed9703f.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/a3ca58a1-b116-45cc-a5d5-6e562b69a54c"]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/32dba52784d5d303.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/fe8e3918-4bec-4737-af5c-a6820222622a"]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/7cf0e8915d7f154c.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/762f6582-616f-4261-89c8-2008f0814e32"]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/6456dbcd21290144.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/474efb40-e7c5-4063-8fa4-e0f351898a60"]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/2b747a67a6e761ac.png)
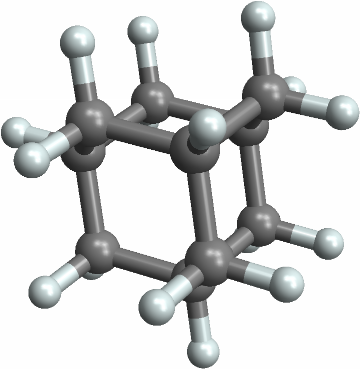
![ResourceFunction[
"PointGroupSymbol"][Molecule[{"C", "C", "C", "C", "C", "C", "H", "H",
"H", "H", "H", "H"}, {
Bond[{1, 2}, "Aromatic"],
Bond[{2, 3}, "Aromatic"],
Bond[{3, 4}, "Aromatic"],
Bond[{4, 5}, "Aromatic"],
Bond[{5, 6}, "Aromatic"],
Bond[{6, 1}, "Aromatic"],
Bond[{1, 7}, "Single"],
Bond[{2, 8}, "Single"],
Bond[{3, 9}, "Single"],
Bond[{4, 10}, "Single"],
Bond[{5, 11}, "Single"],
Bond[{6, 12}, "Single"]}, {}], "ComputeAtomCoordinates" -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/0d680aa4bbba8985.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/59a6ef7d-318d-4b05-953d-fd4f98602d7a"]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/2cf49c8774d4a059.png)
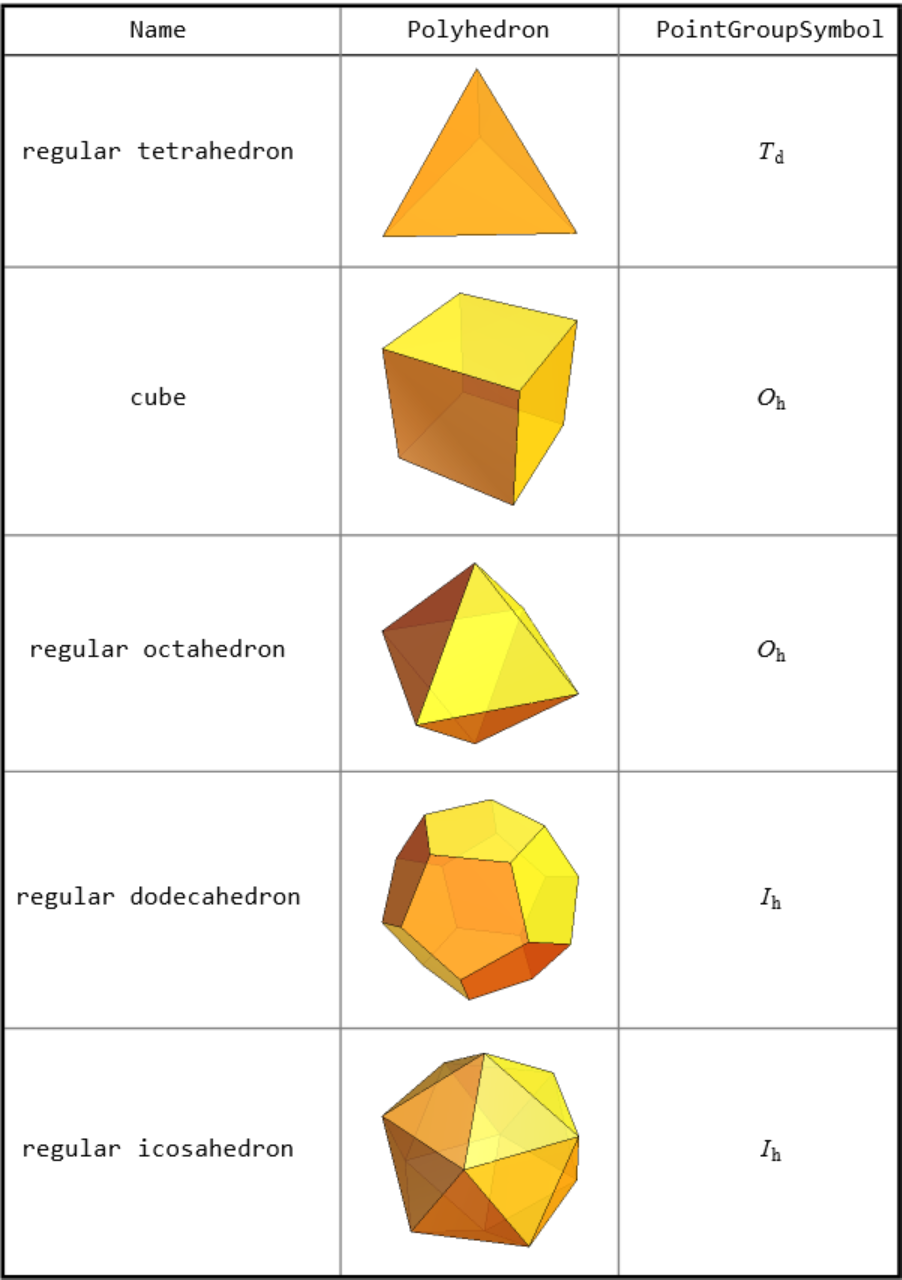
![With[{polyhedra = Entity["Polyhedron", #] & /@ PolyhedronData["Platonic"]},
{#["Name"], Show[#["Graphics3D"], ImageSize -> Tiny], ResourceFunction["PointGroupSymbol"][#]} & /@ polyhedra // RightComposition[Prepend[#, {"Name", "Polyhedron",
InterpretationBox[
TagBox[
TagBox[
DynamicModuleBox[{Typeset`open = False},
FrameBox[
PaneSelectorBox[{False -> GridBox[{{
PaneBox[
GridBox[{{
AdjustmentBox[
StyleBox[
StyleBox[
StyleBox[
"\"[\[FilledSmallSquare]]\"", FontColor -> RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], "ResourceFunctionIcon"], FontFamily -> "Source Sans Pro Black", FontWeight -> "Heavy", PrivateFontOptions -> {"OperatorSubstitution" -> False}, FontSize -> 0.6538461538461539 Inherited, ShowStringCharacters -> False], BoxBaselineShift -> -0.25, BoxMargins -> {{0, 0}, {-1, -1}}],
StyleBox[
RowBox[{
StyleBox[
"PointGroupSymbol", "ResourceFunctionLabel", FontFamily -> "Source Sans Pro"], " "}], FontColor -> GrayLevel[0.1], FontSize -> Rational[12, 13] Inherited, ShowStringCharacters -> False, ShowAutoStyles -> False]}}, GridBoxSpacings -> {"Columns" -> {{0.25}}}], Alignment -> Left, FrameMargins -> {{3, 0}, {0, 0}}, BaselinePosition -> Baseline, BaseStyle -> {LineSpacing -> {0, 0}, LineBreakWithin -> False}],
ItemBox[
PaneBox[
TogglerBox[
Dynamic[Typeset`open], {True -> DynamicBox[
FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False -> DynamicBox[
FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]}, BaselinePosition -> Baseline, Appearance -> None, ContentPadding -> False, FrameMargins -> 0], Alignment -> Left, FrameMargins -> {{1, 1}, {0, 0}},
BaselinePosition -> Baseline], Frame -> {{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}}, GridBoxAlignment -> {"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize -> {"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings -> {"Columns" -> {{0}}, "Rows" -> {{0}}},
BaselinePosition -> {1, 1}], True -> GridBox[{{
GridBox[{{
PaneBox[
GridBox[{{
AdjustmentBox[
StyleBox[
StyleBox[
StyleBox[
"\"[\[FilledSmallSquare]]\"", FontColor -> RGBColor[
0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], "ResourceFunctionIcon"], FontFamily -> "Source Sans Pro Black", FontWeight -> "Heavy", PrivateFontOptions -> {"OperatorSubstitution" -> False}, FontSize -> 0.6538461538461539 Inherited, ShowStringCharacters -> False], BoxBaselineShift -> -0.25, BoxMargins -> {{0, 0}, {-1, -1}}],
StyleBox[
RowBox[{
StyleBox[
"PointGroupSymbol", "ResourceFunctionLabel", FontFamily -> "Source Sans Pro"], " "}], FontColor -> GrayLevel[0.1], FontSize -> Rational[12, 13] Inherited, ShowStringCharacters -> False, ShowAutoStyles -> False]}}, GridBoxSpacings -> {"Columns" -> {{0.25}}}], Alignment -> Left, FrameMargins -> {{3, 0}, {0, 0}}, BaselinePosition -> Baseline, BaseStyle -> {LineSpacing -> {0, 0}, LineBreakWithin -> False}],
ItemBox[
PaneBox[
TogglerBox[
Dynamic[Typeset`open], {True -> DynamicBox[
FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False -> DynamicBox[
FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]}, BaselinePosition -> Baseline, Appearance -> None, ContentPadding -> False, FrameMargins -> 0], Alignment -> Left, FrameMargins -> {{1, 1}, {0, 0}}, BaselinePosition -> Baseline], Frame -> {{
RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]}}, GridBoxAlignment -> {"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize -> {"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings -> {"Columns" -> {{0}}, "Rows" -> {{0}}}, BaselinePosition -> {1, 1}]}, {
StyleBox[
PaneBox[
GridBox[{{
RowBox[{
TagBox["\"Version (latest): \"", "IconizedLabel"], " ",
TagBox["\"1.1.1\"", "IconizedItem"]}]}, {
TagBox[
TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/"}, "HyperlinkURL"], "IconizedItem"]}}, GridBoxAlignment -> {"Columns" -> {{Left}}}, DefaultBaseStyle -> "Column", GridBoxItemSize -> {"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}], Alignment -> Left, FrameMargins -> {{5, 4}, {0, 4}}, BaselinePosition -> Baseline], "DialogStyle", FontFamily -> "Roboto", FontSize -> 11]}}, GridBoxAlignment -> {"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize -> {"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, BaselinePosition -> {1, 1}, GridBoxDividers -> {"Columns" -> {{None}}, "Rows" -> {False, {
GrayLevel[0.8]}, False}}]},
Dynamic[Typeset`open], BaselinePosition -> Baseline, ImageSize -> Automatic], BaselinePosition -> Baseline, FrameMargins -> {{0, 0}, {1, 0}}, FrameStyle -> RGBColor[
0.8313725490196079, 0.8470588235294118, 0.8509803921568627], Background -> RGBColor[
0.9686274509803922, 0.9764705882352941, 0.984313725490196],
RoundingRadius -> 4, DefaultBaseStyle -> {}]], #& , TagBoxNote -> " "], {"FunctionResourceBox",
RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784],
"PointGroupSymbol"}, TagBoxNote -> "FunctionResourceBox"],
ResourceFunction["PointGroupSymbol"], BoxID -> "PointGroupSymbol", Selectable -> False]}]& , Grid[#, Dividers -> {{Thick, {Gray}, Thick}, {Thick, True, {Gray}, Thick}}, Spacings -> {{1, {3}, 1}, {1, 1, {2}}}]& ]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/2916c95fd2f91644.png)
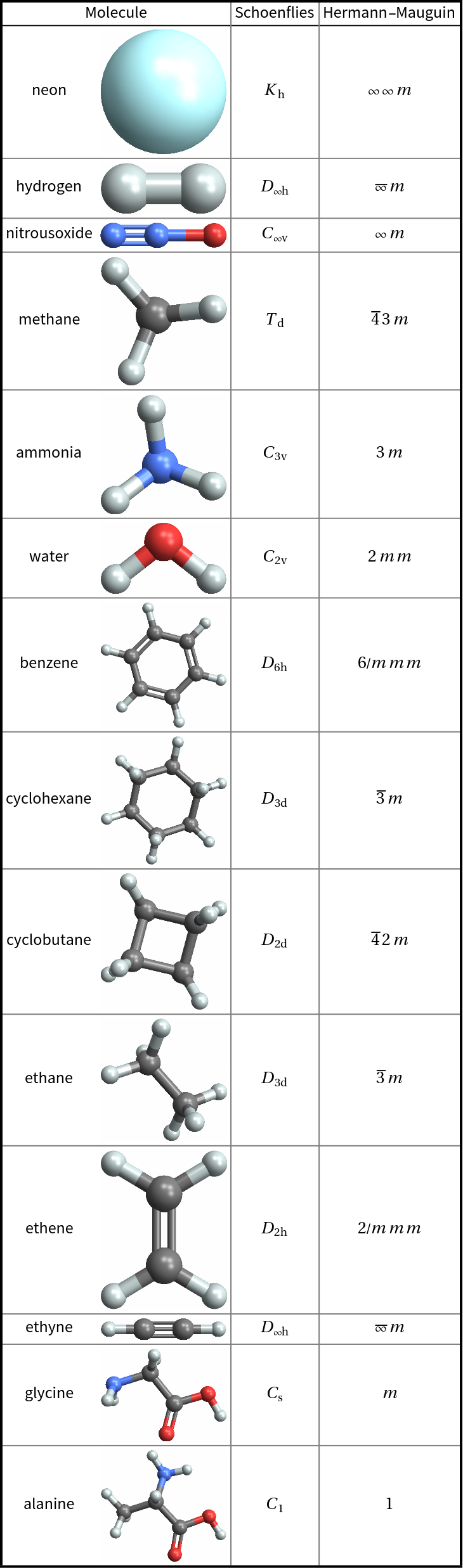
![mols = {"neon", "hydrogen", "nitrousoxide", "methane", "ammonia", "water", "benzene", "cyclohexane", "cyclobutane", "ethane", "ethene", "ethyne", "glycine", "alanine"};
Outer[ResourceFunction["PointGroupSymbol"][Molecule[#1], "SymbolType" -> #2, "ComputeAtomCoordinates" -> Automatic] &, mols, {"Schoenflies", "HermannMauguin"}] // RightComposition[
MapThread[Join[{#,
MoleculePlot3D[
Molecule[#], ImageSize -> Tiny]}, #2]& , {mols, #}]& , Prepend[#, {"Molecule", SpanFromLeft, "Schoenflies", "Hermann-Mauguin"}]& , Grid[#, Dividers -> {{Thick, False, {Gray}, Thick}, {Thick, True, {Gray}, Thick}}]& ]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/1de136f9aad4b51a.png)
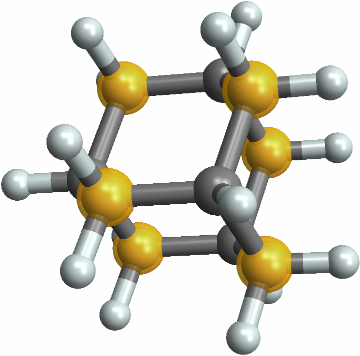
![MoleculePlot3D[
mol = Molecule["C1(O)C(O)C(O)C(O)C(O)C1(O)"] // MoleculeModify[#, "EnergyMinimizeAtomCoordinates"] &, ImageSize -> Small]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/13f7158077982f91.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/19fd96a3-b72c-4c6f-8b7b-d79a3e44ee0b"]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/24dcaf2db00d0c74.png)
![Row[{MoleculePlot3D[mol = Molecule[{
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"]}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Single"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Single"],
Bond[{6, 1}, "Single"],
Bond[{1, 7}, "Single"],
Bond[{1, 8}, "Single"],
Bond[{2, 9}, "Single"],
Bond[{2, 10}, "Single"],
Bond[{3, 11}, "Single"],
Bond[{3, 12}, "Single"],
Bond[{4, 13}, "Single"],
Bond[{4, 14}, "Single"],
Bond[{5, 15}, "Single"],
Bond[{5, 16}, "Single"],
Bond[{6, 17}, "Single"],
Bond[{6, 18}, "Single"]}, AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{18, 3}, {{{1.526, 0, 0}, {0.763, 1.3215547661750533`, 0}, {-0.763,
1.3215547661750533`, 0}, {-1.526, 0, 0}, {-0.763, -1.3215547661750533`, 0}, {0.763, -1.3215547661750533`, 0}, {2.1639720474545365`,
0., 0.9022287219251371}, {2.1639720474545365`, 0., -0.9022287219251371}, {1.0819860237272683`, 1.8740547661750533`, -0.9022287219251371}, {
1.0819860237272683`, 1.8740547661750533`, 0.9022287219251371}, {-1.0819860237272683`, 1.8740547661750533`, -0.9022287219251371}, {-1.0819860237272683`, 1.8740547661750533`, 0.9022287219251371}, {-2.1639720474545365`, 0., -0.9022287219251371}, {-2.1639720474545365`, 0., 0.9022287219251371}, {-1.0819860237272683`, -1.8740547661750533`, -0.9022287219251371}, {-1.0819860237272683`, -1.8740547661750533`, 0.9022287219251371}, {
1.0819860237272683`, -1.8740547661750533`, 0.9022287219251371}, {
1.0819860237272683`, -1.8740547661750533`, -0.9022287219251371}}, "Angstroms", {{1}, {2}}}]], MetaInformation -> <|"Conformation" -> "Planar"|>], ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}, ImageSize -> Small], Style[ResourceFunction["PointGroupSymbol"][mol], 36]}, Spacer[36]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/177889da9610e7ab.png)
![Row[{MoleculePlot3D[mol = Molecule[{
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"]}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Single"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Single"],
Bond[{6, 1}, "Single"],
Bond[{1, 7}, "Single"],
Bond[{1, 8}, "Single"],
Bond[{2, 9}, "Single"],
Bond[{2, 10}, "Single"],
Bond[{3, 11}, "Single"],
Bond[{3, 12}, "Single"],
Bond[{4, 13}, "Single"],
Bond[{4, 14}, "Single"],
Bond[{5, 15}, "Single"],
Bond[{5, 16}, "Single"],
Bond[{6, 17}, "Single"],
Bond[{6, 18}, "Single"]}, AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{18, 3}, {{{1.526, 0, 0.24494897427831783`}, {0.763, 1.3215547661750533`, -0.24494897427831783`}, {-0.763, 1.3215547661750533`, 0.24494897427831783`}, {-1.526, 0, -0.24494897427831783`}, {-0.763, -1.3215547661750533`, 0.24494897427831783`}, {
0.763, -1.3215547661750533`, -0.24494897427831783`}, {
1.5753778830504686`, 0., 1.3488451762218947`}, {
2.5503040258103473`, 0., -0.16957034096370419`}, {
0.7876889415252342, 1.364317267281856, -1.3488451762218947`}, {
1.2751520129051737`, 2.2086280737254858`, 0.16957034096370424`}, {-1.2751520129051737`, 2.2086280737254858`, -0.16957034096370424`}, {-0.7876889415252342, 1.364317267281856, 1.3488451762218947`}, {-1.5753778830504686`, 0., -1.3488451762218947`}, {-2.5503040258103473`, 0., 0.16957034096370419`}, {-1.2751520129051737`, -2.2086280737254858`, -0.16957034096370424`}, {-0.7876889415252342, -1.364317267281856, 1.3488451762218947`}, {
1.2751520129051737`, -2.2086280737254858`, 0.16957034096370424`}, {
0.7876889415252342, -1.364317267281856, -1.3488451762218947`}}, "Angstroms", {{1}, {2}}}]], MetaInformation -> <|"Conformation" -> "Chair"|>], ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}, ImageSize -> Small], Style[ResourceFunction["PointGroupSymbol"][mol], 36]}, Spacer[36]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/12b59fc3eaae16f6.png)
![Row[{MoleculePlot3D[mol = Molecule[{
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"]}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Single"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Single"],
Bond[{6, 1}, "Single"],
Bond[{1, 7}, "Single"],
Bond[{1, 8}, "Single"],
Bond[{2, 9}, "Single"],
Bond[{2, 10}, "Single"],
Bond[{3, 11}, "Single"],
Bond[{3, 12}, "Single"],
Bond[{4, 13}, "Single"],
Bond[{4, 14}, "Single"],
Bond[{5, 15}, "Single"],
Bond[{5, 16}, "Single"],
Bond[{6, 17}, "Single"],
Bond[{6, 18}, "Single"]}, AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{18, 3}, {{{1.526, 0, 0.}, {0.763, 1.3215547661750533`, -0.35}, {-0.763, 1.3215547661750533`, 0.35}, {-1.526, 0, 0.}, {-0.763, -1.3215547661750533`, -0.35}, {
0.763, -1.3215547661750533`, 0.35}, {2.1639720474545365`, 0.2309825804813448, 0.872160371824383}, {
2.1639720474545365`, -0.2309825804813448, -0.872160371824383}, {0.6599089866248756, 1.4024015393960056`, -1.4472060163073523`}, {
1.3377912052691072`, 2.1851525022222216`, 0.030577220337072775`}, {-1.3377912052691072`, 2.1851525022222216`, -0.030577220337072775`}, {-0.6599089866248756, 1.4024015393960056`, 1.4472060163073523`}, {-2.1639720474545365`, 0.2309825804813448, -0.872160371824383}, {-2.1639720474545365`, -0.2309825804813448, 0.872160371824383}, {-0.6599089866248756, -1.4024015393960056`, -1.4472060163073523`}, {-1.3377912052691072`, -2.1851525022222216`, 0.030577220337072775`}, {
0.6599089866248756, -1.4024015393960056`, 1.4472060163073523`}, {
1.3377912052691072`, -2.1851525022222216`, -0.030577220337072775`}}, "Angstroms", {{1}, {2}}}]], MetaInformation -> <|"Conformation" -> "TwistBoat"|>], ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}, ImageSize -> Small], Style[ResourceFunction["PointGroupSymbol"][mol], 36]}, Spacer[36]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/03aeddc81655e87a.png)
![Row[{MoleculePlot3D[mol = Molecule[{
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"]}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Single"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Single"],
Bond[{6, 1}, "Single"],
Bond[{1, 7}, "Single"],
Bond[{1, 8}, "Single"],
Bond[{2, 9}, "Single"],
Bond[{2, 10}, "Single"],
Bond[{3, 11}, "Single"],
Bond[{3, 12}, "Single"],
Bond[{4, 13}, "Single"],
Bond[{4, 14}, "Single"],
Bond[{5, 15}, "Single"],
Bond[{5, 16}, "Single"],
Bond[{6, 17}, "Single"],
Bond[{6, 18}, "Single"]}, AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{18, 3}, {{{1.526, 0, 0.40414518843273806`}, {0.763, 1.3215547661750533`, -0.20207259421636903`}, {-0.763, 1.3215547661750533`, -0.20207259421636903`}, {-1.526, 0, 0.40414518843273806`}, {-0.763, -1.3215547661750533`, -0.20207259421636903`}, {
0.763, -1.3215547661750533`, -0.20207259421636903`}, {
1.4642515864509655`, 0., 1.5074185604598969`}, {
2.5867589150002814`, 0., 0.09460436035439679}, {
1.0930615489444242`, 1.4416151928301804`, -1.2497700065734851`}, {
1.0930615489444242`, 2.193968969439382, 0.3903612264345745}, {-1.0930615489444242`, 1.4416151928301804`, -1.2497700065734851`}, {-1.0930615489444242`, 2.193968969439382, 0.3903612264345745}, {-2.5867589150002814`, 0., 0.09460436035439679}, {-1.4642515864509655`, 0., 1.5074185604598969`}, {-1.0930615489444242`, -1.4416151928301804`, -1.2497700065734851`}, {-1.0930615489444242`, -2.193968969439382, 0.3903612264345745}, {
1.0930615489444242`, -2.193968969439382, 0.3903612264345745}, {
1.0930615489444242`, -1.4416151928301804`, -1.2497700065734851`}}, "Angstroms", {{1}, {2}}}]], MetaInformation -> <|"Conformation" -> "Boat"|>], ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}, ImageSize -> Small], Style[ResourceFunction["PointGroupSymbol"][mol], 36]}, Spacer[36]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/5b421d3d2079e4a4.png)
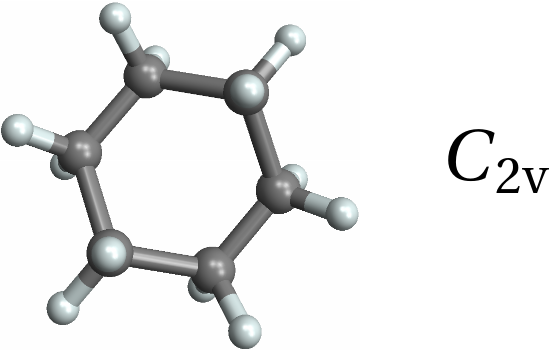
![Row[{MoleculePlot3D[mol = Molecule[{
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"]}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Single"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Single"],
Bond[{6, 1}, "Single"],
Bond[{1, 7}, "Single"],
Bond[{1, 8}, "Single"],
Bond[{2, 9}, "Single"],
Bond[{2, 10}, "Single"],
Bond[{3, 11}, "Single"],
Bond[{3, 12}, "Single"],
Bond[{4, 13}, "Single"],
Bond[{4, 14}, "Single"],
Bond[{5, 15}, "Single"],
Bond[{5, 16}, "Single"],
Bond[{6, 17}, "Single"],
Bond[{6, 18}, "Single"]}, AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{18, 3}, {{{1.526, 0, 0.12247448713915891`}, {0.763, 1.3215547661750533`, -0.27247448713915895`}, {-0.763, 1.3215547661750533`, 0.27247448713915895`}, {-1.526, 0, -0.12247448713915891`}, {-0.763, -1.3215547661750533`, -0.02752551286084111}, {0.763, -1.3215547661750533`, 0.02752551286084111}, {1.8595864467809025`, 0.11298464035772575`, 1.1698424041422184`}, {
2.4079596156902863`, -0.08089455282056494, -0.5383040745707409}, {0.7494499197077007, 1.411149075396593, -1.373752951052436}, {
1.2974777239760091`, 2.186177428750382, 0.1608685801119213}, {-1.2974777239760091`, 2.186177428750382, -0.1608685801119213}, {-0.7494499197077007, 1.411149075396593, 1.373752951052436}, {-1.8595864467809025`, 0.11298464035772575`, -1.1698424041422184`}, {-2.4079596156902863`, -0.08089455282056494, 0.5383040745707409}, {-1.0500055428799022`, -1.9194532150825474`, -0.9113638822193035}, {-1.1149753187981495`, -1.8275720768346213`, 0.8895812727807216}, {
1.0500055428799022`, -1.9194532150825474`, 0.9113638822193035}, {
1.1149753187981495`, -1.8275720768346213`, -0.8895812727807216}}, "Angstroms", {{1}, {2}}}]], MetaInformation -> <|"Conformation" -> "HalfChair"|>], ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}, ImageSize -> Small], Style[ResourceFunction["PointGroupSymbol"][mol], 36]}, Spacer[36]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/55a34c70776d5ab8.png)
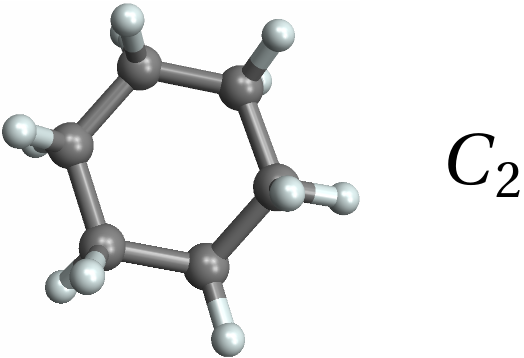
![Row[{MoleculePlot3D[mol = Molecule[{
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["C"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"],
Atom["H"]}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Single"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Single"],
Bond[{6, 1}, "Single"],
Bond[{1, 7}, "Single"],
Bond[{1, 8}, "Single"],
Bond[{2, 9}, "Single"],
Bond[{2, 10}, "Single"],
Bond[{3, 11}, "Single"],
Bond[{3, 12}, "Single"],
Bond[{4, 13}, "Single"],
Bond[{4, 14}, "Single"],
Bond[{5, 15}, "Single"],
Bond[{5, 16}, "Single"],
Bond[{6, 17}, "Single"],
Bond[{6, 18}, "Single"]}, AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{18, 3}, {{{1.526, 0, 0.2379445409770841}, {0.763, 1.3215547661750533`, -0.1802095140581215}, {-0.763, 1.3215547661750533`, 0.06473946022019633}, {-1.526, 0, -0.007004433301233737}, {-0.763, -1.3215547661750533`, 0.06473946022019633}, {
0.763, -1.3215547661750533`, -0.1802095140581215}, {
1.6518543254290639`, 0., 1.3357540366414256`}, {
2.5190732766372985`, 0., -0.24664855351442885`}, {
0.9333717940584856, 1.4845884304248909`, -1.2597550092136358`}, {
1.198542973387693, 2.1603897470089066`, 0.39222667737466743`}, {-1.2114250395503983`, 1.995275278739109, -0.6876172735535169}, {-0.9284038141649422, 1.7361539996082969`, 1.0755678600469207`}, {-2.0767075051325343`, 0., -0.964995165923789}, {-2.2456331560908587`, 0., 0.8315378260123385}, {-1.2114250395503983`, -1.995275278739109, -0.6876172735535169}, {-0.9284038141649422, -1.7361539996082969`, 1.0755678600469207`}, {
1.198542973387693, -2.1603897470089066`, 0.39222667737466743`}, {
0.9333717940584856, -1.4845884304248909`, -1.2597550092136358`}}, "Angstroms", {{1}, {2}}}]], MetaInformation -> <|"Conformation" -> "HalfBoat"|>], ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}, ImageSize -> Small], Style[ResourceFunction["PointGroupSymbol"][mol], 36]}, Spacer[36]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/32a4beefb2c6b567.png)
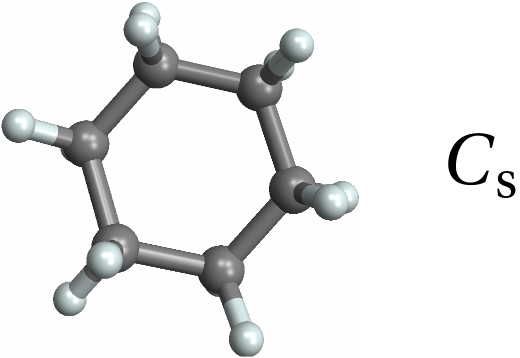
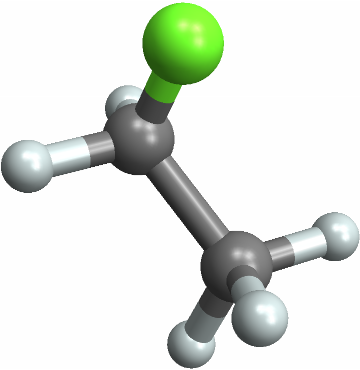
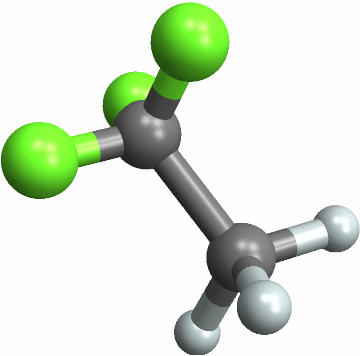
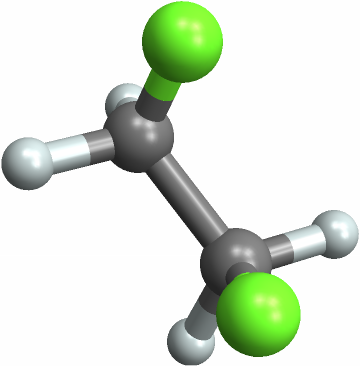
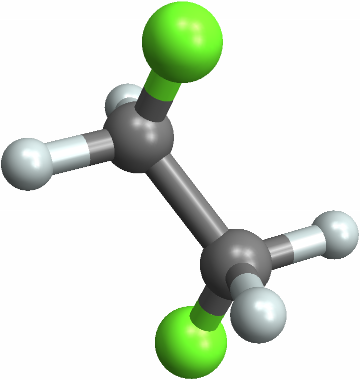
![With[{mol = Molecule[{"C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Double"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Double"],
Bond[{4, 7}, "Double"],
Bond[{7, 8}, "Single"],
Bond[{8, 9}, "Double"],
Bond[{9, 10}, "Single"],
Bond[{10, 11}, "Single"],
Bond[{11, 12}, "Double"],
Bond[{10, 13}, "Double"],
Bond[{13, 14}, "Single"],
Bond[{14, 15}, "Double"],
Bond[{15, 16}, "Single"],
Bond[{16, 17}, "Single"],
Bond[{17, 18}, "Double"],
Bond[{16, 19}, "Double"],
Bond[{19, 20}, "Single"],
Bond[{20, 21}, "Double"],
Bond[{21, 22}, "Single"],
Bond[{22, 23}, "Single"],
Bond[{23, 24}, "Double"],
Bond[{22, 25}, "Double"],
Bond[{25, 26}, "Single"],
Bond[{26, 27}, "Double"],
Bond[{27, 28}, "Single"],
Bond[{28, 29}, "Single"],
Bond[{29, 30}, "Double"],
Bond[{28, 31}, "Double"],
Bond[{31, 32}, "Single"],
Bond[{32, 33}, "Double"],
Bond[{33, 34}, "Single"],
Bond[{34, 35}, "Single"],
Bond[{35, 36}, "Double"],
Bond[{6, 1}, "Single"],
Bond[{12, 7}, "Single"],
Bond[{18, 13}, "Single"],
Bond[{24, 19}, "Single"],
Bond[{30, 25}, "Single"],
Bond[{36, 31}, "Single"],
Bond[{34, 1}, "Double"],
Bond[{2, 37}, "Single"],
Bond[{3, 38}, "Single"],
Bond[{5, 39}, "Single"],
Bond[{6, 40}, "Single"],
Bond[{8, 41}, "Single"],
Bond[{9, 42}, "Single"],
Bond[{11, 43}, "Single"],
Bond[{12, 44}, "Single"],
Bond[{14, 45}, "Single"],
Bond[{15, 46}, "Single"],
Bond[{17, 47}, "Single"],
Bond[{18, 48}, "Single"],
Bond[{20, 49}, "Single"],
Bond[{21, 50}, "Single"],
Bond[{23, 51}, "Single"],
Bond[{24, 52}, "Single"],
Bond[{26, 53}, "Single"],
Bond[{27, 54}, "Single"],
Bond[{29, 55}, "Single"],
Bond[{30, 56}, "Single"],
Bond[{32, 57}, "Single"],
Bond[{33, 58}, "Single"],
Bond[{35, 59}, "Single"],
Bond[{36, 60}, "Single"]}, {AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{60, 3}, {{{4.0325, 0., 0}, {3.9712372640217284`, 0.7002362764418966, 1.212435565298214}, {
3.4922474407607482`, 2.01625, 1.212435565298214}, {3.089074216877279, 2.5920410360609694`,
0}, {3.4922474407607482`, 2.01625, -1.212435565298214}, {
3.9712372640217284`, 0.7002362764418966, -1.212435565298214}, {2.01625, 3.4922474407607482`, 0}, {1.379196227960759, 3.7893104933191757`, 1.212435565298214}, {0., 4.0325, 1.212435565298214}, {-0.7002362764418966, 3.9712372640217284`, 0}, {0., 4.0325, -1.212435565298214}, {1.379196227960759, 3.7893104933191757`, -1.212435565298214}, {-2.01625, 3.4922474407607482`, 0}, {-2.5920410360609694`, 3.089074216877279, 1.212435565298214}, {-3.4922474407607482`, 2.01625, 1.212435565298214}, {-3.7893104933191757`, 1.379196227960759, 0}, {-3.4922474407607482`, 2.01625, -1.212435565298214}, {-2.5920410360609694`, 3.089074216877279, -1.212435565298214}, {-4.0325, 0., 0}, {-3.9712372640217284`, -0.7002362764418966, 1.212435565298214}, {-3.4922474407607482`, -2.01625, 1.212435565298214}, {-3.089074216877279, -2.5920410360609694`, 0}, {-3.4922474407607482`, -2.01625, -1.212435565298214}, {-3.9712372640217284`, -0.7002362764418966, -1.212435565298214}, {-2.01625, -3.4922474407607482`, 0}, {-1.379196227960759, -3.7893104933191757`, 1.212435565298214}, {0., -4.0325, 1.212435565298214}, {0.7002362764418966, -3.9712372640217284`, 0}, {
0., -4.0325, -1.212435565298214}, {-1.379196227960759, -3.7893104933191757`, -1.212435565298214}, {2.01625, -3.4922474407607482`, 0}, {2.5920410360609694`, -3.089074216877279, 1.212435565298214}, {3.4922474407607482`, -2.01625, 1.212435565298214}, {3.7893104933191757`, -1.379196227960759, 0}, {
3.4922474407607482`, -2.01625, -1.212435565298214}, {
2.5920410360609694`, -3.089074216877279, -1.212435565298214}, {4.029251398299003, 0.16183145338754712`, 2.1477430013854075`}, {3.190608896691404, 2.465982789549364,
2.1477430013854075`}, {3.190608896691404, 2.465982789549364, -2.1477430013854075`}, {
4.029251398299003, 0.16183145338754712`, -2.1477430013854075`}, {
1.874475549384529, 3.5703497958546815`, 2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, 2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, -2.1477430013854075`}, {
1.874475549384529, 3.5703497958546815`, -2.1477430013854075`}, {-2.154775848914474, 3.408518342467135, 2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, 2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, -2.1477430013854075`}, {-2.154775848914474, 3.408518342467135, -2.1477430013854075`}, {-4.029251398299003, -0.16183145338754729`, 2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, 2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, -2.1477430013854075`}, {-4.029251398299003, -0.16183145338754729`, -2.1477430013854075`}, {-1.8744755493845295`, -3.570349795854681, 2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, 2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, -2.1477430013854075`}, {-1.8744755493845295`, -3.570349795854681, -2.1477430013854075`}, {2.1547758489144755`, -3.408518342467134, 2.1477430013854075`}, {
3.730908189390666, -1.5301569633007128`, 2.1477430013854075`}, {
3.730908189390666, -1.5301569633007128`, -2.1477430013854075`}, {
2.1547758489144755`, -3.408518342467134, -2.1477430013854075`}}, "Angstroms", {{1}, {2}}}]]}]}, Show[MoleculePlot3D[mol, ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}], Graphics3D[
Text[Style[ResourceFunction["PointGroupSymbol"][mol], 36], {0, 0, 0}]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/38462edb8f04e7fe.png)
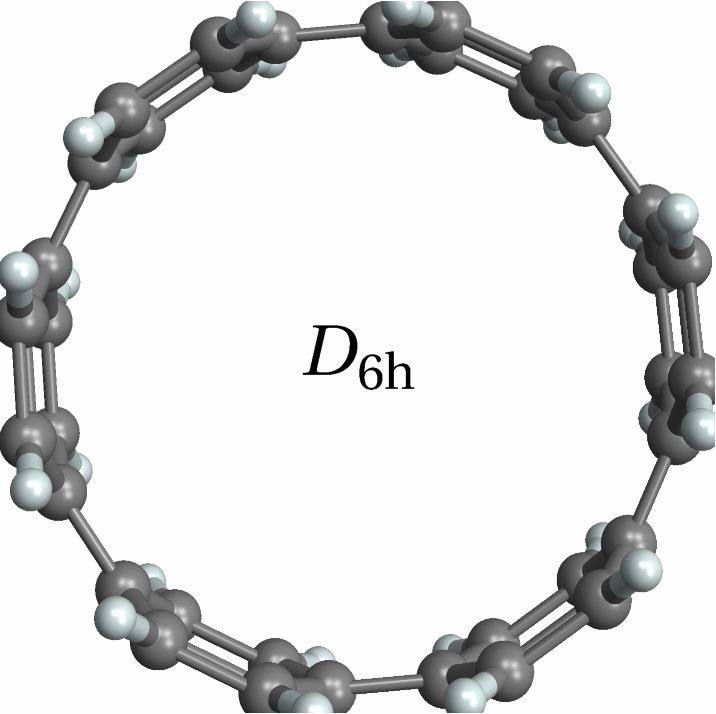
![With[{mol = Molecule[{"C", "N", "C", "C", "C", "C", "C", "N", "C", "C", "C", "C", "C", "N", "C", "C", "C", "C", "C", "N", "C", "C", "C", "C", "C", "N", "C", "C", "C", "C", "C", "N", "C", "C", "C", "C", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Double"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Double"],
Bond[{4, 7}, "Double"],
Bond[{7, 8}, "Single"],
Bond[{8, 9}, "Double"],
Bond[{9, 10}, "Single"],
Bond[{10, 11}, "Single"],
Bond[{11, 12}, "Double"],
Bond[{10, 13}, "Double"],
Bond[{13, 14}, "Single"],
Bond[{14, 15}, "Double"],
Bond[{15, 16}, "Single"],
Bond[{16, 17}, "Single"],
Bond[{17, 18}, "Double"],
Bond[{16, 19}, "Double"],
Bond[{19, 20}, "Single"],
Bond[{20, 21}, "Double"],
Bond[{21, 22}, "Single"],
Bond[{22, 23}, "Single"],
Bond[{23, 24}, "Double"],
Bond[{22, 25}, "Double"],
Bond[{25, 26}, "Single"],
Bond[{26, 27}, "Double"],
Bond[{27, 28}, "Single"],
Bond[{28, 29}, "Single"],
Bond[{29, 30}, "Double"],
Bond[{28, 31}, "Double"],
Bond[{31, 32}, "Single"],
Bond[{32, 33}, "Double"],
Bond[{33, 34}, "Single"],
Bond[{34, 35}, "Single"],
Bond[{35, 36}, "Double"],
Bond[{6, 1}, "Single"],
Bond[{12, 7}, "Single"],
Bond[{18, 13}, "Single"],
Bond[{24, 19}, "Single"],
Bond[{30, 25}, "Single"],
Bond[{36, 31}, "Single"],
Bond[{34, 1}, "Double"],
Bond[{3, 37}, "Single"],
Bond[{5, 38}, "Single"],
Bond[{6, 39}, "Single"],
Bond[{9, 40}, "Single"],
Bond[{11, 41}, "Single"],
Bond[{12, 42}, "Single"],
Bond[{15, 43}, "Single"],
Bond[{17, 44}, "Single"],
Bond[{18, 45}, "Single"],
Bond[{21, 46}, "Single"],
Bond[{23, 47}, "Single"],
Bond[{24, 48}, "Single"],
Bond[{27, 49}, "Single"],
Bond[{29, 50}, "Single"],
Bond[{30, 51}, "Single"],
Bond[{33, 52}, "Single"],
Bond[{35, 53}, "Single"],
Bond[{36, 54}, "Single"]}, {AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{54, 3}, {{{4.0325, 0., 0}, {3.9712372640217284`, 0.7002362764418966, 1.212435565298214}, {
3.4922474407607482`, 2.01625, 1.212435565298214}, {3.089074216877279, 2.5920410360609694`,
0}, {3.4922474407607482`, 2.01625, -1.212435565298214}, {
3.9712372640217284`, 0.7002362764418966, -1.212435565298214}, {2.01625, 3.4922474407607482`, 0}, {1.379196227960759, 3.7893104933191757`, 1.212435565298214}, {0., 4.0325, 1.212435565298214}, {-0.7002362764418966, 3.9712372640217284`, 0}, {0., 4.0325, -1.212435565298214}, {1.379196227960759, 3.7893104933191757`, -1.212435565298214}, {-2.01625, 3.4922474407607482`, 0}, {-2.5920410360609694`, 3.089074216877279, 1.212435565298214}, {-3.4922474407607482`, 2.01625, 1.212435565298214}, {-3.7893104933191757`, 1.379196227960759, 0}, {-3.4922474407607482`, 2.01625, -1.212435565298214}, {-2.5920410360609694`, 3.089074216877279, -1.212435565298214}, {-4.0325, 0., 0}, {-3.9712372640217284`, -0.7002362764418966, 1.212435565298214}, {-3.4922474407607482`, -2.01625, 1.212435565298214}, {-3.089074216877279, -2.5920410360609694`, 0}, {-3.4922474407607482`, -2.01625, -1.212435565298214}, {-3.9712372640217284`, -0.7002362764418966, -1.212435565298214}, {-2.01625, -3.4922474407607482`, 0}, {-1.379196227960759, -3.7893104933191757`, 1.212435565298214}, {0., -4.0325, 1.212435565298214}, {0.7002362764418966, -3.9712372640217284`, 0}, {
0., -4.0325, -1.212435565298214}, {-1.379196227960759, -3.7893104933191757`, -1.212435565298214}, {2.01625, -3.4922474407607482`, 0}, {2.5920410360609694`, -3.089074216877279, 1.212435565298214}, {3.4922474407607482`, -2.01625, 1.212435565298214}, {3.7893104933191757`, -1.379196227960759, 0}, {
3.4922474407607482`, -2.01625, -1.212435565298214}, {
2.5920410360609694`, -3.089074216877279, -1.212435565298214}, {3.190608896691404, 2.465982789549364, 2.1477430013854075`}, {3.190608896691404, 2.465982789549364, -2.1477430013854075`}, {
4.029251398299003, 0.16183145338754712`, -2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, 2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, -2.1477430013854075`}, {
1.874475549384529, 3.5703497958546815`, -2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, 2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, -2.1477430013854075`}, {-2.154775848914474, 3.408518342467135, -2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, 2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, -2.1477430013854075`}, {-4.029251398299003, -0.16183145338754729`, -2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, 2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, -2.1477430013854075`}, {-1.8744755493845295`, -3.570349795854681, -2.1477430013854075`}, {3.730908189390666, -1.5301569633007128`, 2.1477430013854075`}, {
3.730908189390666, -1.5301569633007128`, -2.1477430013854075`}, {
2.1547758489144755`, -3.408518342467134, -2.1477430013854075`}}, "Angstroms", {{1}, {2}}}]]}]}, Show[MoleculePlot3D[mol, ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}], Graphics3D[{Text[
Style[ResourceFunction["PointGroupSymbol"][mol], 36], {0, 0, 0}],
Sequence[{
Inset[1, {3.8536286355368525`, 0.6687511324120635, 0.}],
Inset[2, {3.822997267547717, 1.0188692706330118`, 0.606217782649107}],
Inset[3, {3.5835023559172265`, 1.6768761324120636`, 0.606217782649107}],
Inset[4, {3.381915743975492, 1.964771650442548, 0.}],
Inset[5, {3.5835023559172265`, 1.6768761324120636`, -0.606217782649107}],
Inset[6, {3.822997267547717, 1.0188692706330118`, -0.606217782649107}]}]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/625e5c18b220103c.png)
![With[{mol = Molecule[{"C", "N", "C", "C", "C", "C", "C", "C", "C", "C", "C", "N", "C", "N", "C", "C", "C", "C", "C", "C", "C", "C", "C", "N", "C", "N", "C", "C", "C", "C", "C", "C", "C", "C", "C", "N", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Double"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Double"],
Bond[{4, 7}, "Double"],
Bond[{7, 8}, "Single"],
Bond[{8, 9}, "Double"],
Bond[{9, 10}, "Single"],
Bond[{10, 11}, "Single"],
Bond[{11, 12}, "Double"],
Bond[{10, 13}, "Double"],
Bond[{13, 14}, "Single"],
Bond[{14, 15}, "Double"],
Bond[{15, 16}, "Single"],
Bond[{16, 17}, "Single"],
Bond[{17, 18}, "Double"],
Bond[{16, 19}, "Double"],
Bond[{19, 20}, "Single"],
Bond[{20, 21}, "Double"],
Bond[{21, 22}, "Single"],
Bond[{22, 23}, "Single"],
Bond[{23, 24}, "Double"],
Bond[{22, 25}, "Double"],
Bond[{25, 26}, "Single"],
Bond[{26, 27}, "Double"],
Bond[{27, 28}, "Single"],
Bond[{28, 29}, "Single"],
Bond[{29, 30}, "Double"],
Bond[{28, 31}, "Double"],
Bond[{31, 32}, "Single"],
Bond[{32, 33}, "Double"],
Bond[{33, 34}, "Single"],
Bond[{34, 35}, "Single"],
Bond[{35, 36}, "Double"],
Bond[{6, 1}, "Single"],
Bond[{12, 7}, "Single"],
Bond[{18, 13}, "Single"],
Bond[{24, 19}, "Single"],
Bond[{30, 25}, "Single"],
Bond[{36, 31}, "Single"],
Bond[{34, 1}, "Double"],
Bond[{3, 37}, "Single"],
Bond[{5, 38}, "Single"],
Bond[{6, 39}, "Single"],
Bond[{8, 40}, "Single"],
Bond[{9, 41}, "Single"],
Bond[{11, 42}, "Single"],
Bond[{15, 43}, "Single"],
Bond[{17, 44}, "Single"],
Bond[{18, 45}, "Single"],
Bond[{20, 46}, "Single"],
Bond[{21, 47}, "Single"],
Bond[{23, 48}, "Single"],
Bond[{27, 49}, "Single"],
Bond[{29, 50}, "Single"],
Bond[{30, 51}, "Single"],
Bond[{32, 52}, "Single"],
Bond[{33, 53}, "Single"],
Bond[{35, 54}, "Single"]}, {AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{54, 3}, {{{4.0325, 0., 0}, {3.9712372640217284`, 0.7002362764418966, 1.212435565298214}, {
3.4922474407607482`, 2.01625, 1.212435565298214}, {3.089074216877279, 2.5920410360609694`,
0}, {3.4922474407607482`, 2.01625, -1.212435565298214}, {
3.9712372640217284`, 0.7002362764418966, -1.212435565298214}, {2.01625, 3.4922474407607482`, 0}, {1.379196227960759, 3.7893104933191757`, 1.212435565298214}, {0., 4.0325, 1.212435565298214}, {-0.7002362764418966, 3.9712372640217284`, 0}, {0., 4.0325, -1.212435565298214}, {1.379196227960759, 3.7893104933191757`, -1.212435565298214}, {-2.01625, 3.4922474407607482`, 0}, {-2.5920410360609694`, 3.089074216877279, 1.212435565298214}, {-3.4922474407607482`, 2.01625, 1.212435565298214}, {-3.7893104933191757`, 1.379196227960759, 0}, {-3.4922474407607482`, 2.01625, -1.212435565298214}, {-2.5920410360609694`, 3.089074216877279, -1.212435565298214}, {-4.0325, 0., 0}, {-3.9712372640217284`, -0.7002362764418966, 1.212435565298214}, {-3.4922474407607482`, -2.01625, 1.212435565298214}, {-3.089074216877279, -2.5920410360609694`, 0}, {-3.4922474407607482`, -2.01625, -1.212435565298214}, {-3.9712372640217284`, -0.7002362764418966, -1.212435565298214}, {-2.01625, -3.4922474407607482`, 0}, {-1.379196227960759, -3.7893104933191757`, 1.212435565298214}, {0., -4.0325, 1.212435565298214}, {0.7002362764418966, -3.9712372640217284`, 0}, {
0., -4.0325, -1.212435565298214}, {-1.379196227960759, -3.7893104933191757`, -1.212435565298214}, {2.01625, -3.4922474407607482`, 0}, {2.5920410360609694`, -3.089074216877279, 1.212435565298214}, {3.4922474407607482`, -2.01625, 1.212435565298214}, {3.7893104933191757`, -1.379196227960759, 0}, {
3.4922474407607482`, -2.01625, -1.212435565298214}, {
2.5920410360609694`, -3.089074216877279, -1.212435565298214}, {3.190608896691404, 2.465982789549364, 2.1477430013854075`}, {3.190608896691404, 2.465982789549364, -2.1477430013854075`}, {
4.029251398299003, 0.16183145338754712`, -2.1477430013854075`}, {
1.874475549384529, 3.5703497958546815`, 2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, 2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, -2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, 2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, -2.1477430013854075`}, {-2.154775848914474, 3.408518342467135, -2.1477430013854075`}, {-4.029251398299003, -0.16183145338754729`, 2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, 2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, -2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, 2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, -2.1477430013854075`}, {-1.8744755493845295`, -3.570349795854681, -2.1477430013854075`}, {2.1547758489144755`, -3.408518342467134, 2.1477430013854075`}, {
3.730908189390666, -1.5301569633007128`, 2.1477430013854075`}, {
3.730908189390666, -1.5301569633007128`, -2.1477430013854075`}}, "Angstroms", {{1}, {2}}}]]}]}, Show[MoleculePlot3D[mol, ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}], Graphics3D[{Text[
Style[ResourceFunction["PointGroupSymbol"][mol], 36], {0, 0, 0}],
Sequence[{
Inset[1, {3.8536286355368525`, 0.6687511324120635, 0.}],
Inset[2, {3.822997267547717, 1.0188692706330118`, 0.606217782649107}],
Inset[3, {3.5835023559172265`, 1.6768761324120636`, 0.606217782649107}],
Inset[4, {3.381915743975492, 1.964771650442548, 0.}],
Inset[5, {3.5835023559172265`, 1.6768761324120636`, -0.606217782649107}],
Inset[6, {3.822997267547717, 1.0188692706330118`, -0.606217782649107}]}]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/4d835aeb253e5851.png)
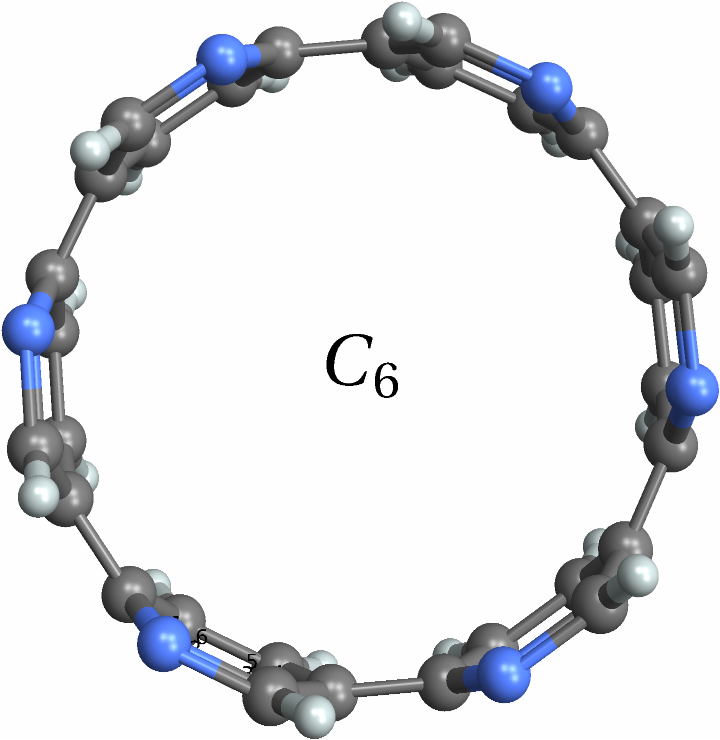
![With[{mol = Molecule[{"C", "N", "C", "C", "C", "N", "C", "N", "C", "C", "C", "N", "C", "N", "C", "C", "C", "N", "C", "N", "C", "C", "C", "N", "C", "N", "C", "C", "C", "N", "C", "N", "C", "C", "C", "N", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Double"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Double"],
Bond[{4, 7}, "Double"],
Bond[{7, 8}, "Single"],
Bond[{8, 9}, "Double"],
Bond[{9, 10}, "Single"],
Bond[{10, 11}, "Single"],
Bond[{11, 12}, "Double"],
Bond[{10, 13}, "Double"],
Bond[{13, 14}, "Single"],
Bond[{14, 15}, "Double"],
Bond[{15, 16}, "Single"],
Bond[{16, 17}, "Single"],
Bond[{17, 18}, "Double"],
Bond[{16, 19}, "Double"],
Bond[{19, 20}, "Single"],
Bond[{20, 21}, "Double"],
Bond[{21, 22}, "Single"],
Bond[{22, 23}, "Single"],
Bond[{23, 24}, "Double"],
Bond[{22, 25}, "Double"],
Bond[{25, 26}, "Single"],
Bond[{26, 27}, "Double"],
Bond[{27, 28}, "Single"],
Bond[{28, 29}, "Single"],
Bond[{29, 30}, "Double"],
Bond[{28, 31}, "Double"],
Bond[{31, 32}, "Single"],
Bond[{32, 33}, "Double"],
Bond[{33, 34}, "Single"],
Bond[{34, 35}, "Single"],
Bond[{35, 36}, "Double"],
Bond[{6, 1}, "Single"],
Bond[{12, 7}, "Single"],
Bond[{18, 13}, "Single"],
Bond[{24, 19}, "Single"],
Bond[{30, 25}, "Single"],
Bond[{36, 31}, "Single"],
Bond[{34, 1}, "Double"],
Bond[{3, 37}, "Single"],
Bond[{5, 38}, "Single"],
Bond[{9, 39}, "Single"],
Bond[{11, 40}, "Single"],
Bond[{15, 41}, "Single"],
Bond[{17, 42}, "Single"],
Bond[{21, 43}, "Single"],
Bond[{23, 44}, "Single"],
Bond[{27, 45}, "Single"],
Bond[{29, 46}, "Single"],
Bond[{33, 47}, "Single"],
Bond[{35, 48}, "Single"]}, {AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{48, 3}, {{{4.0325, 0., 0}, {3.9712372640217284`, 0.7002362764418966, 1.212435565298214}, {
3.4922474407607482`, 2.01625, 1.212435565298214}, {3.089074216877279, 2.5920410360609694`,
0}, {3.4922474407607482`, 2.01625, -1.212435565298214}, {
3.9712372640217284`, 0.7002362764418966, -1.212435565298214}, {2.01625, 3.4922474407607482`, 0}, {1.379196227960759, 3.7893104933191757`, 1.212435565298214}, {0., 4.0325, 1.212435565298214}, {-0.7002362764418966, 3.9712372640217284`, 0}, {0., 4.0325, -1.212435565298214}, {1.379196227960759, 3.7893104933191757`, -1.212435565298214}, {-2.01625, 3.4922474407607482`, 0}, {-2.5920410360609694`, 3.089074216877279, 1.212435565298214}, {-3.4922474407607482`, 2.01625, 1.212435565298214}, {-3.7893104933191757`, 1.379196227960759, 0}, {-3.4922474407607482`, 2.01625, -1.212435565298214}, {-2.5920410360609694`, 3.089074216877279, -1.212435565298214}, {-4.0325, 0., 0}, {-3.9712372640217284`, -0.7002362764418966, 1.212435565298214}, {-3.4922474407607482`, -2.01625, 1.212435565298214}, {-3.089074216877279, -2.5920410360609694`, 0}, {-3.4922474407607482`, -2.01625, -1.212435565298214}, {-3.9712372640217284`, -0.7002362764418966, -1.212435565298214}, {-2.01625, -3.4922474407607482`, 0}, {-1.379196227960759, -3.7893104933191757`, 1.212435565298214}, {0., -4.0325, 1.212435565298214}, {0.7002362764418966, -3.9712372640217284`, 0}, {
0., -4.0325, -1.212435565298214}, {-1.379196227960759, -3.7893104933191757`, -1.212435565298214}, {2.01625, -3.4922474407607482`, 0}, {2.5920410360609694`, -3.089074216877279, 1.212435565298214}, {3.4922474407607482`, -2.01625, 1.212435565298214}, {3.7893104933191757`, -1.379196227960759, 0}, {
3.4922474407607482`, -2.01625, -1.212435565298214}, {
2.5920410360609694`, -3.089074216877279, -1.212435565298214}, {3.190608896691404, 2.465982789549364, 2.1477430013854075`}, {3.190608896691404, 2.465982789549364, -2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, 2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, -2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, 2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, -2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, 2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, -2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, 2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, -2.1477430013854075`}, {3.730908189390666, -1.5301569633007128`, 2.1477430013854075`}, {
3.730908189390666, -1.5301569633007128`, -2.1477430013854075`}}, "Angstroms", {{1}, {2}}}]]}]}, Show[MoleculePlot3D[mol, ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}], Graphics3D[{Text[
Style[ResourceFunction["PointGroupSymbol"][mol], 36], {0, 0, 0}],
Sequence[{
Inset[1, {3.8536286355368525`, 0.6687511324120635, 0.}],
Inset[2, {3.822997267547717, 1.0188692706330118`, 0.606217782649107}],
Inset[3, {3.5835023559172265`, 1.6768761324120636`, 0.606217782649107}],
Inset[4, {3.381915743975492, 1.964771650442548, 0.}],
Inset[5, {3.5835023559172265`, 1.6768761324120636`, -0.606217782649107}],
Inset[6, {3.822997267547717, 1.0188692706330118`, -0.606217782649107}]}]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/5441b0444cd7c8bf.png)
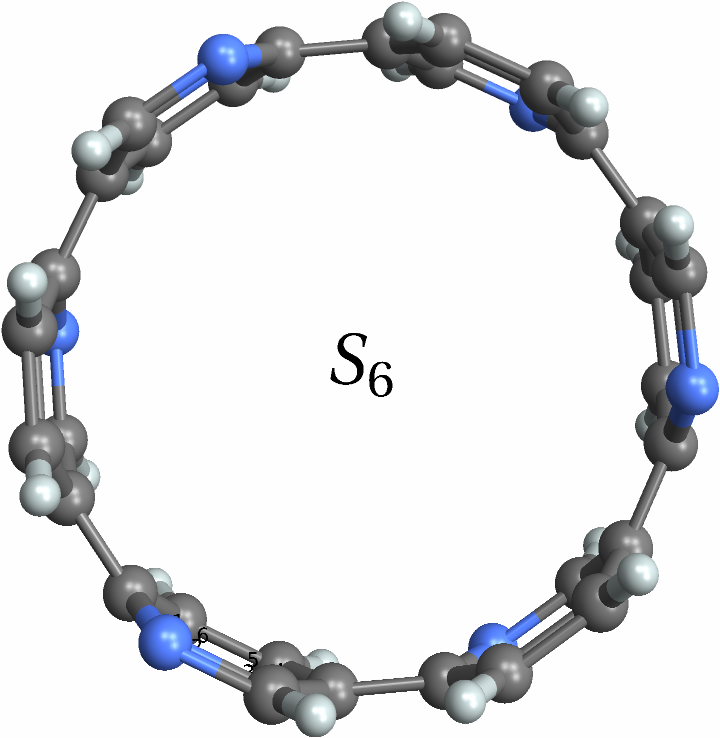
![With[{mol = Molecule[{"C", "N", "N", "C", "C", "C", "C", "N", "N", "C", "C", "C", "C", "N", "N", "C", "C", "C", "C", "N", "N", "C", "C", "C", "C", "N", "N", "C", "C", "C", "C", "N", "N", "C", "C", "C", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Double"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Double"],
Bond[{4, 7}, "Double"],
Bond[{7, 8}, "Single"],
Bond[{8, 9}, "Double"],
Bond[{9, 10}, "Single"],
Bond[{10, 11}, "Single"],
Bond[{11, 12}, "Double"],
Bond[{10, 13}, "Double"],
Bond[{13, 14}, "Single"],
Bond[{14, 15}, "Double"],
Bond[{15, 16}, "Single"],
Bond[{16, 17}, "Single"],
Bond[{17, 18}, "Double"],
Bond[{16, 19}, "Double"],
Bond[{19, 20}, "Single"],
Bond[{20, 21}, "Double"],
Bond[{21, 22}, "Single"],
Bond[{22, 23}, "Single"],
Bond[{23, 24}, "Double"],
Bond[{22, 25}, "Double"],
Bond[{25, 26}, "Single"],
Bond[{26, 27}, "Double"],
Bond[{27, 28}, "Single"],
Bond[{28, 29}, "Single"],
Bond[{29, 30}, "Double"],
Bond[{28, 31}, "Double"],
Bond[{31, 32}, "Single"],
Bond[{32, 33}, "Double"],
Bond[{33, 34}, "Single"],
Bond[{34, 35}, "Single"],
Bond[{35, 36}, "Double"],
Bond[{6, 1}, "Single"],
Bond[{12, 7}, "Single"],
Bond[{18, 13}, "Single"],
Bond[{24, 19}, "Single"],
Bond[{30, 25}, "Single"],
Bond[{36, 31}, "Single"],
Bond[{34, 1}, "Double"],
Bond[{5, 37}, "Single"],
Bond[{6, 38}, "Single"],
Bond[{11, 39}, "Single"],
Bond[{12, 40}, "Single"],
Bond[{17, 41}, "Single"],
Bond[{18, 42}, "Single"],
Bond[{23, 43}, "Single"],
Bond[{24, 44}, "Single"],
Bond[{29, 45}, "Single"],
Bond[{30, 46}, "Single"],
Bond[{35, 47}, "Single"],
Bond[{36, 48}, "Single"]}, {AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{48, 3}, {{{4.0325, 0., 0}, {3.9712372640217284`, 0.7002362764418966, 1.212435565298214}, {
3.4922474407607482`, 2.01625, 1.212435565298214}, {3.089074216877279, 2.5920410360609694`,
0}, {3.4922474407607482`, 2.01625, -1.212435565298214}, {
3.9712372640217284`, 0.7002362764418966, -1.212435565298214}, {2.01625, 3.4922474407607482`, 0}, {1.379196227960759, 3.7893104933191757`, 1.212435565298214}, {0., 4.0325, 1.212435565298214}, {-0.7002362764418966, 3.9712372640217284`, 0}, {0., 4.0325, -1.212435565298214}, {1.379196227960759, 3.7893104933191757`, -1.212435565298214}, {-2.01625, 3.4922474407607482`, 0}, {-2.5920410360609694`, 3.089074216877279, 1.212435565298214}, {-3.4922474407607482`, 2.01625, 1.212435565298214}, {-3.7893104933191757`, 1.379196227960759, 0}, {-3.4922474407607482`, 2.01625, -1.212435565298214}, {-2.5920410360609694`, 3.089074216877279, -1.212435565298214}, {-4.0325, 0., 0}, {-3.9712372640217284`, -0.7002362764418966, 1.212435565298214}, {-3.4922474407607482`, -2.01625, 1.212435565298214}, {-3.089074216877279, -2.5920410360609694`, 0}, {-3.4922474407607482`, -2.01625, -1.212435565298214}, {-3.9712372640217284`, -0.7002362764418966, -1.212435565298214}, {-2.01625, -3.4922474407607482`, 0}, {-1.379196227960759, -3.7893104933191757`, 1.212435565298214}, {0., -4.0325, 1.212435565298214}, {0.7002362764418966, -3.9712372640217284`, 0}, {
0., -4.0325, -1.212435565298214}, {-1.379196227960759, -3.7893104933191757`, -1.212435565298214}, {2.01625, -3.4922474407607482`, 0}, {2.5920410360609694`, -3.089074216877279, 1.212435565298214}, {3.4922474407607482`, -2.01625, 1.212435565298214}, {3.7893104933191757`, -1.379196227960759, 0}, {
3.4922474407607482`, -2.01625, -1.212435565298214}, {
2.5920410360609694`, -3.089074216877279, -1.212435565298214}, {3.190608896691404, 2.465982789549364, -2.1477430013854075`}, {
4.029251398299003, 0.16183145338754712`, -2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, -2.1477430013854075`}, {
1.874475549384529, 3.5703497958546815`, -2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, -2.1477430013854075`}, {-2.154775848914474, 3.408518342467135, -2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, -2.1477430013854075`}, {-4.029251398299003, -0.16183145338754729`, -2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, -2.1477430013854075`}, {-1.8744755493845295`, -3.570349795854681, -2.1477430013854075`}, {
3.730908189390666, -1.5301569633007128`, -2.1477430013854075`}, {
2.1547758489144755`, -3.408518342467134, -2.1477430013854075`}}, "Angstroms", {{1}, {2}}}]]}]}, Show[MoleculePlot3D[mol, ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}], Graphics3D[{Text[
Style[ResourceFunction["PointGroupSymbol"][mol], 36], {0, 0, 0}],
Sequence[{
Inset[1, {3.8536286355368525`, 0.6687511324120635, 0.}],
Inset[2, {3.822997267547717, 1.0188692706330118`, 0.606217782649107}],
Inset[3, {3.5835023559172265`, 1.6768761324120636`, 0.606217782649107}],
Inset[4, {3.381915743975492, 1.964771650442548, 0.}],
Inset[5, {3.5835023559172265`, 1.6768761324120636`, -0.606217782649107}],
Inset[6, {3.822997267547717, 1.0188692706330118`, -0.606217782649107}]}]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/1924fa2e252d285b.png)
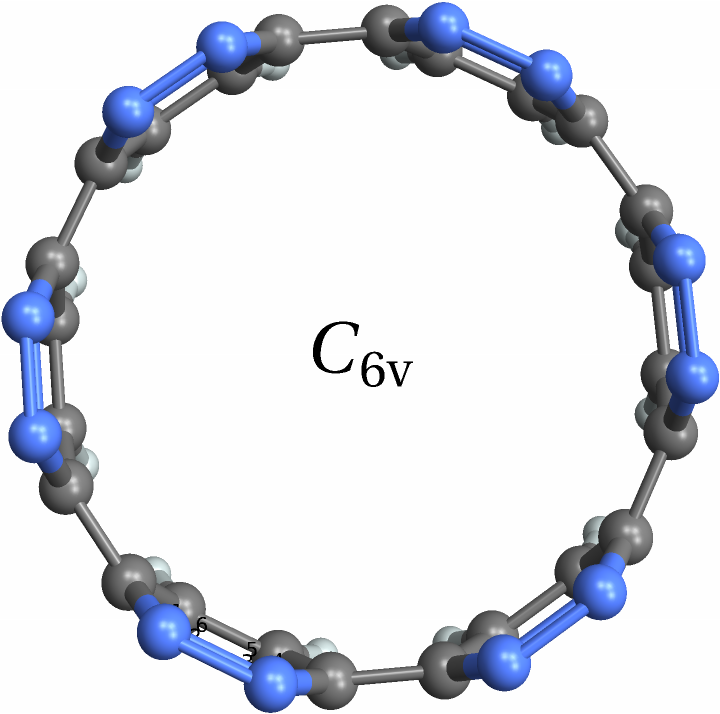
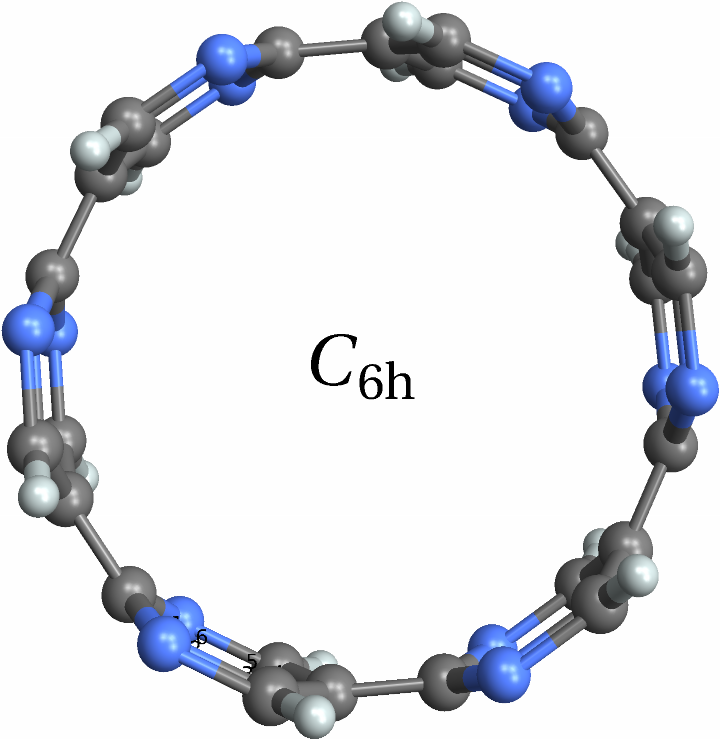
![With[{mol = Molecule[{"C", "N", "C", "C", "N", "C", "C", "N", "C", "C", "N", "C", "C", "N", "C", "C", "N", "C", "C", "N", "C", "C", "N", "C", "C", "N", "C", "C", "N", "C", "C", "N", "C", "C", "N", "C", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Double"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Double"],
Bond[{4, 7}, "Double"],
Bond[{7, 8}, "Single"],
Bond[{8, 9}, "Double"],
Bond[{9, 10}, "Single"],
Bond[{10, 11}, "Single"],
Bond[{11, 12}, "Double"],
Bond[{10, 13}, "Double"],
Bond[{13, 14}, "Single"],
Bond[{14, 15}, "Double"],
Bond[{15, 16}, "Single"],
Bond[{16, 17}, "Single"],
Bond[{17, 18}, "Double"],
Bond[{16, 19}, "Double"],
Bond[{19, 20}, "Single"],
Bond[{20, 21}, "Double"],
Bond[{21, 22}, "Single"],
Bond[{22, 23}, "Single"],
Bond[{23, 24}, "Double"],
Bond[{22, 25}, "Double"],
Bond[{25, 26}, "Single"],
Bond[{26, 27}, "Double"],
Bond[{27, 28}, "Single"],
Bond[{28, 29}, "Single"],
Bond[{29, 30}, "Double"],
Bond[{28, 31}, "Double"],
Bond[{31, 32}, "Single"],
Bond[{32, 33}, "Double"],
Bond[{33, 34}, "Single"],
Bond[{34, 35}, "Single"],
Bond[{35, 36}, "Double"],
Bond[{6, 1}, "Single"],
Bond[{12, 7}, "Single"],
Bond[{18, 13}, "Single"],
Bond[{24, 19}, "Single"],
Bond[{30, 25}, "Single"],
Bond[{36, 31}, "Single"],
Bond[{34, 1}, "Double"],
Bond[{3, 37}, "Single"],
Bond[{6, 38}, "Single"],
Bond[{9, 39}, "Single"],
Bond[{12, 40}, "Single"],
Bond[{15, 41}, "Single"],
Bond[{18, 42}, "Single"],
Bond[{21, 43}, "Single"],
Bond[{24, 44}, "Single"],
Bond[{27, 45}, "Single"],
Bond[{30, 46}, "Single"],
Bond[{33, 47}, "Single"],
Bond[{36, 48}, "Single"]}, {AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{48, 3}, {{{4.0325, 0., 0}, {3.9712372640217284`, 0.7002362764418966, 1.212435565298214}, {
3.4922474407607482`, 2.01625, 1.212435565298214}, {3.089074216877279, 2.5920410360609694`,
0}, {3.4922474407607482`, 2.01625, -1.212435565298214}, {
3.9712372640217284`, 0.7002362764418966, -1.212435565298214}, {2.01625, 3.4922474407607482`, 0}, {1.379196227960759, 3.7893104933191757`, 1.212435565298214}, {0., 4.0325, 1.212435565298214}, {-0.7002362764418966, 3.9712372640217284`, 0}, {0., 4.0325, -1.212435565298214}, {1.379196227960759, 3.7893104933191757`, -1.212435565298214}, {-2.01625, 3.4922474407607482`, 0}, {-2.5920410360609694`, 3.089074216877279, 1.212435565298214}, {-3.4922474407607482`, 2.01625, 1.212435565298214}, {-3.7893104933191757`, 1.379196227960759, 0}, {-3.4922474407607482`, 2.01625, -1.212435565298214}, {-2.5920410360609694`, 3.089074216877279, -1.212435565298214}, {-4.0325, 0., 0}, {-3.9712372640217284`, -0.7002362764418966, 1.212435565298214}, {-3.4922474407607482`, -2.01625, 1.212435565298214}, {-3.089074216877279, -2.5920410360609694`, 0}, {-3.4922474407607482`, -2.01625, -1.212435565298214}, {-3.9712372640217284`, -0.7002362764418966, -1.212435565298214}, {-2.01625, -3.4922474407607482`, 0}, {-1.379196227960759, -3.7893104933191757`, 1.212435565298214}, {0., -4.0325, 1.212435565298214}, {0.7002362764418966, -3.9712372640217284`, 0}, {
0., -4.0325, -1.212435565298214}, {-1.379196227960759, -3.7893104933191757`, -1.212435565298214}, {2.01625, -3.4922474407607482`, 0}, {2.5920410360609694`, -3.089074216877279, 1.212435565298214}, {3.4922474407607482`, -2.01625, 1.212435565298214}, {3.7893104933191757`, -1.379196227960759, 0}, {
3.4922474407607482`, -2.01625, -1.212435565298214}, {
2.5920410360609694`, -3.089074216877279, -1.212435565298214}, {3.190608896691404, 2.465982789549364, 2.1477430013854075`}, {4.029251398299003, 0.16183145338754712`, -2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, 2.1477430013854075`}, {
1.874475549384529, 3.5703497958546815`, -2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, 2.1477430013854075`}, {-2.154775848914474, 3.408518342467135, -2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, 2.1477430013854075`}, {-4.029251398299003, -0.16183145338754729`, -2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, 2.1477430013854075`}, {-1.8744755493845295`, -3.570349795854681, -2.1477430013854075`}, {
3.730908189390666, -1.5301569633007128`, 2.1477430013854075`}, {
2.1547758489144755`, -3.408518342467134, -2.1477430013854075`}}, "Angstroms", {{1}, {2}}}]]}]}, Show[MoleculePlot3D[mol, ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}], Graphics3D[{Text[
Style[ResourceFunction["PointGroupSymbol"][mol], 36], {0, 0, 0}],
Sequence[{
Inset[1, {3.8536286355368525`, 0.6687511324120635, 0.}],
Inset[2, {3.822997267547717, 1.0188692706330118`, 0.606217782649107}],
Inset[3, {3.5835023559172265`, 1.6768761324120636`, 0.606217782649107}],
Inset[4, {3.381915743975492, 1.964771650442548, 0.}],
Inset[5, {3.5835023559172265`, 1.6768761324120636`, -0.606217782649107}],
Inset[6, {3.822997267547717, 1.0188692706330118`, -0.606217782649107}]}]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/3c1bb8ad5feb9cf4.png)
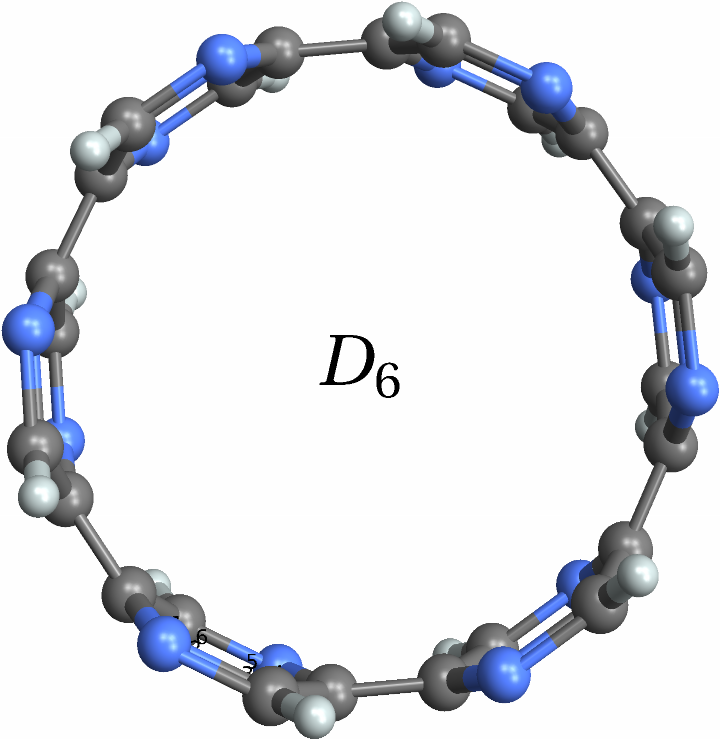
![With[{mol = Molecule[{"C", "N", "N", "C", "C", "C", "C", "C", "C", "C", "N", "N", "C", "N", "N", "C", "C", "C", "C", "C", "C", "C", "N", "N", "C", "N", "N", "C", "C", "C", "C", "C", "C", "C", "N", "N", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H", "H"}, {
Bond[{1, 2}, "Single"],
Bond[{2, 3}, "Double"],
Bond[{3, 4}, "Single"],
Bond[{4, 5}, "Single"],
Bond[{5, 6}, "Double"],
Bond[{4, 7}, "Double"],
Bond[{7, 8}, "Single"],
Bond[{8, 9}, "Double"],
Bond[{9, 10}, "Single"],
Bond[{10, 11}, "Single"],
Bond[{11, 12}, "Double"],
Bond[{10, 13}, "Double"],
Bond[{13, 14}, "Single"],
Bond[{14, 15}, "Double"],
Bond[{15, 16}, "Single"],
Bond[{16, 17}, "Single"],
Bond[{17, 18}, "Double"],
Bond[{16, 19}, "Double"],
Bond[{19, 20}, "Single"],
Bond[{20, 21}, "Double"],
Bond[{21, 22}, "Single"],
Bond[{22, 23}, "Single"],
Bond[{23, 24}, "Double"],
Bond[{22, 25}, "Double"],
Bond[{25, 26}, "Single"],
Bond[{26, 27}, "Double"],
Bond[{27, 28}, "Single"],
Bond[{28, 29}, "Single"],
Bond[{29, 30}, "Double"],
Bond[{28, 31}, "Double"],
Bond[{31, 32}, "Single"],
Bond[{32, 33}, "Double"],
Bond[{33, 34}, "Single"],
Bond[{34, 35}, "Single"],
Bond[{35, 36}, "Double"],
Bond[{6, 1}, "Single"],
Bond[{12, 7}, "Single"],
Bond[{18, 13}, "Single"],
Bond[{24, 19}, "Single"],
Bond[{30, 25}, "Single"],
Bond[{36, 31}, "Single"],
Bond[{34, 1}, "Double"],
Bond[{5, 37}, "Single"],
Bond[{6, 38}, "Single"],
Bond[{8, 39}, "Single"],
Bond[{9, 40}, "Single"],
Bond[{17, 41}, "Single"],
Bond[{18, 42}, "Single"],
Bond[{20, 43}, "Single"],
Bond[{21, 44}, "Single"],
Bond[{29, 45}, "Single"],
Bond[{30, 46}, "Single"],
Bond[{32, 47}, "Single"],
Bond[{33, 48}, "Single"]}, {AtomCoordinates -> QuantityArray[
StructuredArray`StructuredData[{48, 3}, {{{4.0325, 0., 0}, {3.9712372640217284`, 0.7002362764418966, 1.212435565298214}, {
3.4922474407607482`, 2.01625, 1.212435565298214}, {3.089074216877279, 2.5920410360609694`,
0}, {3.4922474407607482`, 2.01625, -1.212435565298214}, {
3.9712372640217284`, 0.7002362764418966, -1.212435565298214}, {2.01625, 3.4922474407607482`, 0}, {1.379196227960759, 3.7893104933191757`, 1.212435565298214}, {0., 4.0325, 1.212435565298214}, {-0.7002362764418966, 3.9712372640217284`, 0}, {0., 4.0325, -1.212435565298214}, {1.379196227960759, 3.7893104933191757`, -1.212435565298214}, {-2.01625, 3.4922474407607482`, 0}, {-2.5920410360609694`, 3.089074216877279, 1.212435565298214}, {-3.4922474407607482`, 2.01625, 1.212435565298214}, {-3.7893104933191757`, 1.379196227960759, 0}, {-3.4922474407607482`, 2.01625, -1.212435565298214}, {-2.5920410360609694`, 3.089074216877279, -1.212435565298214}, {-4.0325, 0., 0}, {-3.9712372640217284`, -0.7002362764418966, 1.212435565298214}, {-3.4922474407607482`, -2.01625, 1.212435565298214}, {-3.089074216877279, -2.5920410360609694`, 0}, {-3.4922474407607482`, -2.01625, -1.212435565298214}, {-3.9712372640217284`, -0.7002362764418966, -1.212435565298214}, {-2.01625, -3.4922474407607482`, 0}, {-1.379196227960759, -3.7893104933191757`, 1.212435565298214}, {0., -4.0325, 1.212435565298214}, {0.7002362764418966, -3.9712372640217284`, 0}, {
0., -4.0325, -1.212435565298214}, {-1.379196227960759, -3.7893104933191757`, -1.212435565298214}, {2.01625, -3.4922474407607482`, 0}, {2.5920410360609694`, -3.089074216877279, 1.212435565298214}, {3.4922474407607482`, -2.01625, 1.212435565298214}, {3.7893104933191757`, -1.379196227960759, 0}, {
3.4922474407607482`, -2.01625, -1.212435565298214}, {
2.5920410360609694`, -3.089074216877279, -1.212435565298214}, {3.190608896691404, 2.465982789549364, -2.1477430013854075`}, {
4.029251398299003, 0.16183145338754712`, -2.1477430013854075`}, {
1.874475549384529, 3.5703497958546815`, 2.1477430013854075`}, {-0.5402992926992619, 3.9961397528500773`, 2.1477430013854075`}, {-3.7309081893906657`, 1.530156963300714, -2.1477430013854075`}, {-2.154775848914474, 3.408518342467135, -2.1477430013854075`}, {-4.029251398299003, -0.16183145338754729`, 2.1477430013854075`}, {-3.190608896691404, -2.4659827895493636`, 2.1477430013854075`}, {
0.5402992926992604, -3.9961397528500777`, -2.1477430013854075`}, {-1.8744755493845295`, -3.570349795854681, -2.1477430013854075`}, {2.1547758489144755`, -3.408518342467134, 2.1477430013854075`}, {
3.730908189390666, -1.5301569633007128`, 2.1477430013854075`}}, "Angstroms", {{1}, {2}}}]]}]}, Show[MoleculePlot3D[mol, ViewCenter -> {0, 0, 0}, ViewVertical -> {0, 0, 10}], Graphics3D[{Text[
Style[ResourceFunction["PointGroupSymbol"][mol], 36], {0, 0, 0}],
Sequence[{
Inset[1, {3.8536286355368525`, 0.6687511324120635, 0.}],
Inset[2, {3.822997267547717, 1.0188692706330118`, 0.606217782649107}],
Inset[3, {3.5835023559172265`, 1.6768761324120636`, 0.606217782649107}],
Inset[4, {3.381915743975492, 1.964771650442548, 0.}],
Inset[5, {3.5835023559172265`, 1.6768761324120636`, -0.606217782649107}],
Inset[6, {3.822997267547717, 1.0188692706330118`, -0.606217782649107}]}]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/3a198dd7d954e4e4.png)
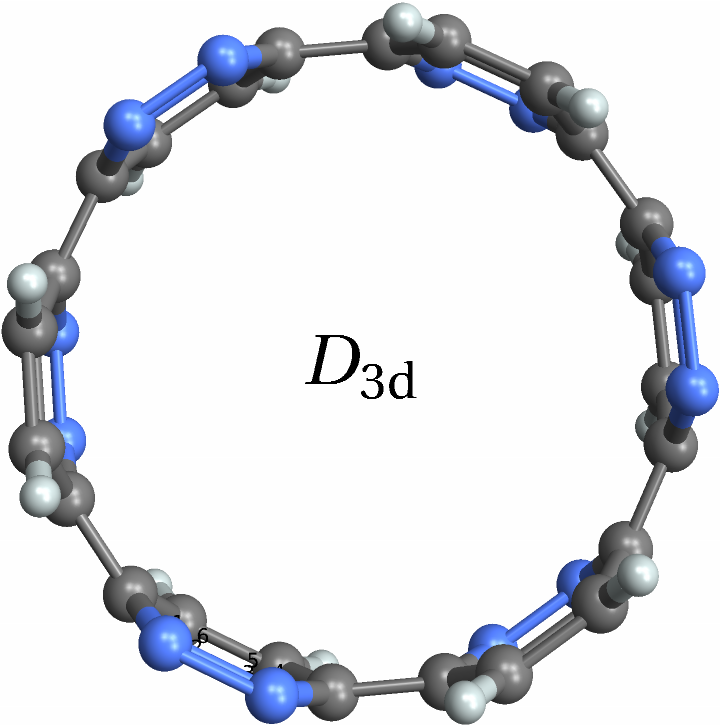
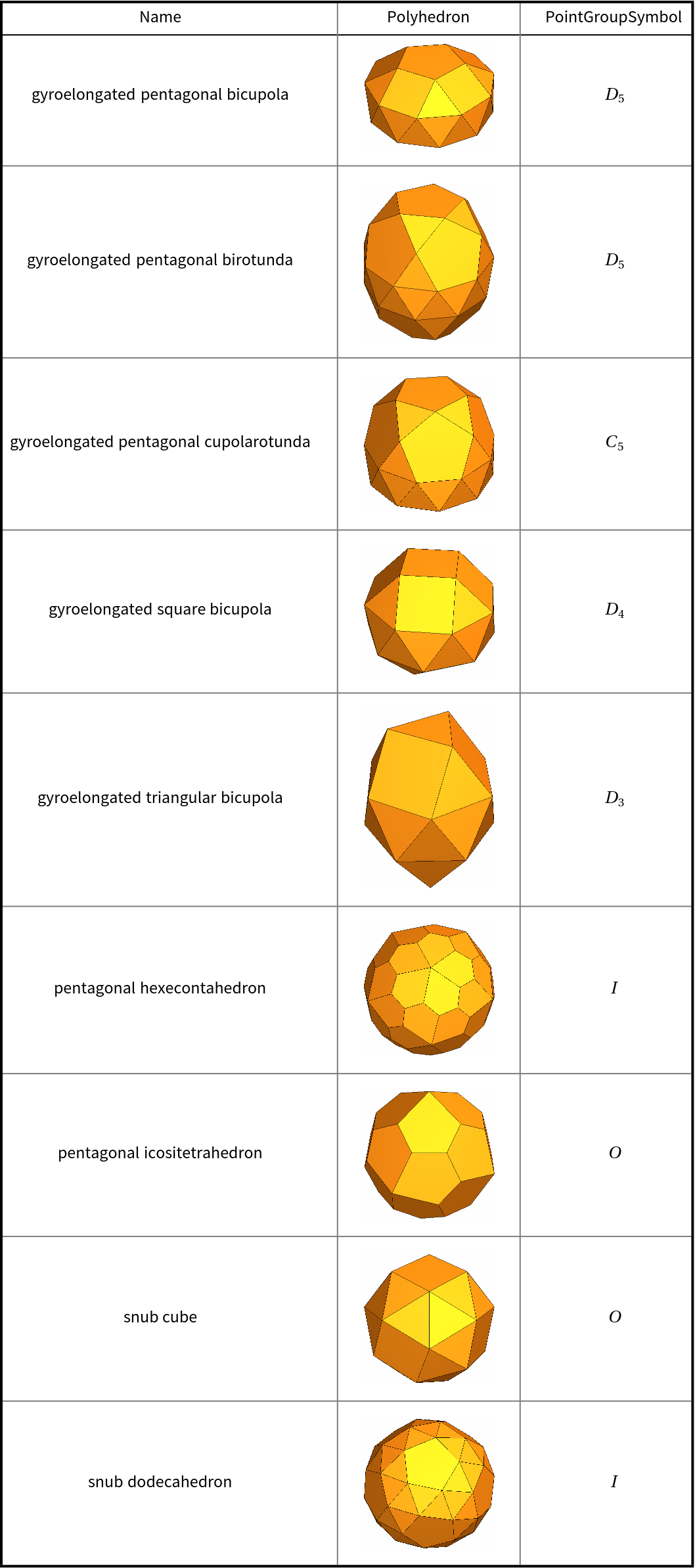
![With[{polyhedra = EntityList@EntityClass["Polyhedron", "Chiral"]},
{#["Name"], Show[#["Graphics3D"], ImageSize -> Tiny], ResourceFunction["PointGroupSymbol"][#]} & /@ polyhedra // RightComposition[
Prepend[#, {"Name", "Polyhedron", "PointGroupSymbol"}]& , Grid[#, Dividers -> {{Thick, {Gray}, Thick}, {Thick, True, {Gray}, Thick}}, Spacings -> {{1, {3}, 1}, {1, 1, {2}}}]& ]]](https://www.wolframcloud.com/obj/resourcesystem/images/01b/01b1cd47-a107-4e93-a3cb-c1a61b8a621a/798640b4692d0fdb.png)