Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PlaneLineIntersection

Source Notebook

Compute the intersection point of a plane and line

Contributed by: Ed Pegg Jr

ResourceFunction["PlaneLineIntersection"][plane,line]

computes the intersection of the given plane and line.

Details

The intersection is a point in three dimensions.
The plane can be provided as three points or as an InfinitePlane. The line can be provided as two points or an InfiniteLine.

Examples

Basic Examples (2) 

Find the intersection of a plane and a line:

In[1]:=
ResourceFunction[ "PlaneLineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{{0, 0, 1}, {0, 1, 0}, {1, 0, 0}}, {{0, 0, 0}, {1, 1, 1}}]
Out[1]=

Find the intersection using InfinitePlane and InfiniteLine:

In[2]:=
ResourceFunction[ "PlaneLineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ InfinitePlane[{{0, 0, 1}, {0, 1, 0}, {1, 0, 0}}], InfiniteLine[{{0, 0, 0}, {1, 1, 1}}]]
Out[2]=

An equivalent specification:

In[3]:=
ResourceFunction[ "PlaneLineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ InfinitePlane[{0, 0, 1}, {{0, 1, -1}, {1, 0, -1}}], InfiniteLine[{{0, 0, 0}, {1, 1, 1}}]]
Out[3]=

Another equivalent specification:

In[4]:=
ResourceFunction[ "PlaneLineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ InfinitePlane[{0, 0, 1}, {{0, 1, -1}, {1, 0, -1}}], InfiniteLine[{0, 0, 0}, {-1, -1, -1}]]
Out[4]=

Applications (2) 

Find the cevians of the circumcenter in a tetrahedron:

In[5]:=
tet = {{0, 0, 0}, {1, 2, 0}, {3, 0, 0}, {1, 1, 2}}; oo = Circumsphere[tet][[1]]; cevians = Table[ResourceFunction[ "PlaneLineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Drop[tet, {k}], {tet[[k]], oo}], {k, 1, 4}]
Out[6]=

Show the cevians:

In[7]:=
Graphics3D[{Sphere[cevians, .05], Opacity[.5], Tetrahedron[tet], InfiniteLine@# & /@ Transpose[{tet, cevians}]}]
Out[7]=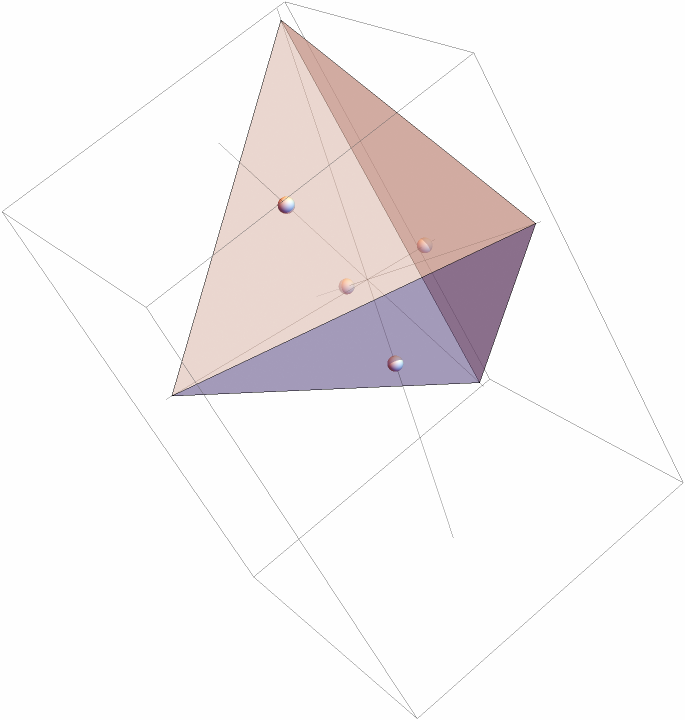

Find the intersection of a line and one face of the d120:

In[8]:=
vert = PolyhedronData["DisdyakisTriacontahedron", "VertexCoordinates"]; face = PolyhedronData["DisdyakisTriacontahedron", "FaceIndices"]; N[ResourceFunction[ "PlaneLineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][vert[[face[[1]]]], {{0, 0, 0}, {1, 2, 3}}]]
Out[10]=

Find intersections for all 120 infinite planes and find the time required:

In[11]:=
Timing[pli = Table[ResourceFunction[ "PlaneLineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][ N[vert[[face[[k]]]]], {{0, 0, 0}, {1, 2, 3}}], {k, 1, 120}];]
Out[11]=

Find intersections for all 120 planes with RegionIntersection and find the time required:

In[12]:=
Timing[ri = Table[RegionIntersection[InfinitePlane[N[vert[[face[[k]]]]]], InfiniteLine[{{0, 0, 0}, {1, 2, 3}}]][[1]], {k, 1, 120}];]
Out[12]=

Check for equality:

In[13]:=
Union[Chop[pli - ri]]
Out[13]=

Possible Issues (1) 

PlaneLineIntersection returns an empty set if the plane and line are parallel, or the line falls in the plane:

In[14]:=
ResourceFunction[ "PlaneLineIntersection", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{{0, 0, 1}, {0, 1, 0}, {0, 1, 1}}, {{1, 0, 0}, {1, 0, 1}}]
Out[14]=

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.1.0 – 27 October 2023
  • 1.0.0 – 20 October 2023

Related Resources

License Information