Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PlanarPolygonFragmentation

Source Notebook

Decompose a pair of polygons into disjoint fragments

Contributed by: Bradley Klee

ResourceFunction["PlanarPolygonFragmentation"][p1,p2]

combines simple polygons p1 and p2 to obtain a pair of disjoint polygonal fragments.

Details

To fragment polygons p1 and p2, we join their combined edge and vertex sets, adding new vertices wherever an edge of p1 crosses an edge of p2. The new set of edges and vertices bounds a finite set of simple polygons (i.e. topological disks), also called “fragments” of p1 and p2.
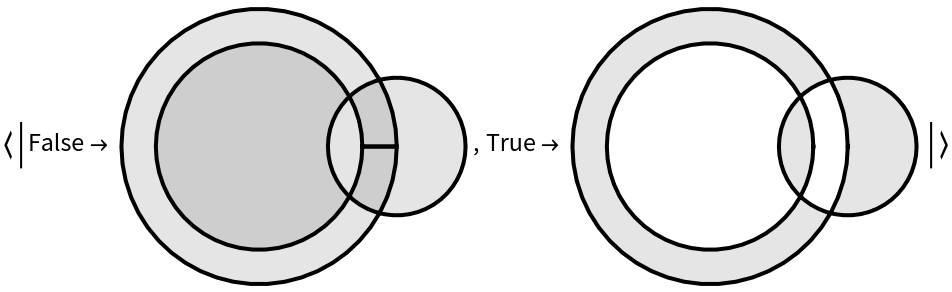
Fragments are extracted and returned in two classes. One class contains the intersection(s) and union of p1 and p2, while the other contains the pairwise complements between p1 and p2.
If the vertices of p1 and p2, have the same circularity (or handedness), then the intersection/union class falls under the True key, while differences fall under the False key.
If the circularity of p1 and p2 are opposite, then the True/False keys are transposed.
There are several polygon clipping algorithms. Transposition for opposite-handedness is consistent with set operations when considering circularity as the determining measure of whether the polygon's filled area is either interior or exterior to the boundary. Such a convention is relatively common in high-power clipping algorithms, and it is also a feature of the wedge product in symplectic geometry.
If the combination of p1 and p2 encloses a polygonal hole, it will become a fragment in the same class as the intersection(s). In this case the union needs a more complicated form, Polygon[frag1→frag2], where frag1 and frag2 are outer and inner boundaries respectively. Considering the outer boundary as enclosing the figure's exterior (including the point at infinity), the union of all fragments should be an exact cover of the entire plane.
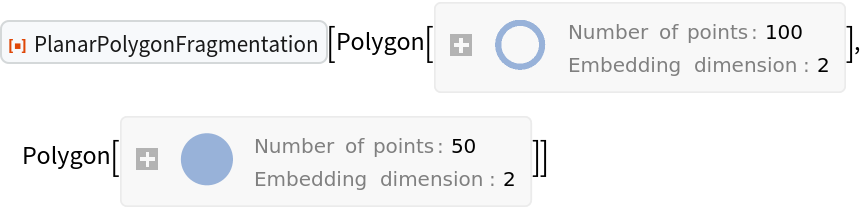
ResourceFunction["PlanarPolygonFragmentation"] takes one option "BinCount" → n, with default value n = 1. When n is set to a positive integer greater than 1, the input vertices and edges are discretized into approximately n2 bins, which allows intersections to be solved locally. For polygons with many edge segments, this saves considerable time by avoiding unnecessary, brute force calculation via Outer. This improves speed, but in pathological cases can lead to incorrect results.
Even in cases where discretization is necessary, a law of diminishing returns applies. There is usually a best choice for "BinCount", which may require experimentation or heuristics to find. In the case of inputs with few edges, setting "BinCount" greater than 1 is not necessary.
Self-intersecting polygons and polygons with holes are not valid inputs. Should one desire, they can be broken up into lists of simple polygons, which can then be folded through the fragmentation process.
Due to the undecidability of zero testing, exact coincidence calculations often need to be evaluated numerically. Currently, all such calculations are done at MachinePrecision, with zero-threshold set to 26$MachineEpsilon. PrecisionGoal may be added as an option in a future version.
ResourceFunction["PlanarPolygonFragmentation"] can be used to solve planar clipping problems. Our algorithm is already more powerful and can be faster than the numerical standard Greiner-Hormann. In utilizing discrete methods, ResourceFunction["PlanarPolygonFragmentation"] goes below the naive order O(n*m) complexity limit, which was carried through the subsequent work "Clipping simple polygons with degenerate intersections" (see references below).

Examples

Basic Examples (2) 

A Venn diagram formed from two polygons:

In[1]:=
{p1, p2} = { Polygon[CirclePoints[{0, 0}, {1, 0}, 10]], Polygon[CirclePoints[{1/2, 0}, {1, 0}, 10]] }; Graphics[{Opacity[.5], Green, p1, Cyan, p2}]
Out[2]=

Fragment into separate regions:

In[3]:=
ResourceFunction["PlanarPolygonFragmentation"][p1, p2]
Out[3]=

Scope (4) 

Coincident vertices are not problematic:

In[4]:=
ResourceFunction["PlanarPolygonFragmentation"][ Polygon[{{1, 1}, {-1, 1}, {-1, -1}, {1, -1}}], Polygon[{{1, 1}, {1/2, 3/2}, {0, 1}, {1/2, 1/2}}] ]
Out[4]=

Obtain the union of two adjacent hexagons:

In[5]:=
res = ResourceFunction["PlanarPolygonFragmentation"][ Polygon[CirclePoints[{0, 0}, {1/2, Pi/6}, 6]], Polygon[CirclePoints[{Sqrt[3]/2, 1/5}, {1/2, Pi/6}, 6]] ]
Out[5]=

The union happens to be the first of the True element:

In[6]:=
Graphics@First[res[True]]
Out[6]=

Specify the order of points in the polygon:

In[7]:=
ResourceFunction["PlanarPolygonFragmentation"][ Polygon[CirclePoints[{0, 0}, {1/2, Pi/6}, 6], Range[6]], Polygon[CirclePoints[{1/2, 0}, {1/2, 2 Pi/5}, 4], Range[4]] ]
Out[7]=

Concave polygons can lead to hole fragments:

In[8]:=
Graphics[concave = Polygon[{{-3, 4}, {-1, 4}, {-1, 6}, {1, 6}, {1, 4}, {3, 4}, {3, 8}, {-3, 8}}]]
Out[8]=
In[9]:=
Graphics[ convex = Polygon[CirclePoints[{0, 1/2}, {4 Sqrt[2], Pi/4}, 4]]]
Out[9]=

Get the boundary and hole:

In[10]:=
{boundary, hole} = ResourceFunction["PlanarPolygonFragmentation"][concave, convex][ True][[{4, 2}]];

The union is then written as:

In[11]:=
Graphics@Polygon[boundary[[1]] -> hole[[1]]]
Out[11]=

Options (3) 

Get the outline of France:

In[12]:=
franceMainland = Polygon[Reverse@Last[CountryData["France", "Shape"][[1]]][[1, 1]]]
Out[12]=

Create an intersecting circle:

In[13]:=
cutWith = Polygon[N@CirclePoints[{0.06, 0}, {.1, 0}, 1000]]
Out[13]=

Difficult cases with many vertices can still be computed efficiently by setting “BinCount”.

In[14]:=
AbsoluteTiming[ With[{res = ResourceFunction["PlanarPolygonFragmentation"][ franceMainland, cutWith, "BinCount" -> 100]}, Graphics@res[True][[2]] ]]
Out[14]=

Changing the discretization parameter only affects timings:

In[15]:=
AbsoluteTiming[ With[{res = ResourceFunction["PlanarPolygonFragmentation"][ franceMainland, cutWith, "BinCount" -> 1000]}, Graphics@res[True][[2]] ] ]
Out[15]=

Properties and Relations (4) 

Get the union by choosing the region with the largest area:

In[16]:=
p1 = ReverseSortBy[ResourceFunction["PlanarPolygonFragmentation"][ Polygon[CirclePoints[{0, 0}, {1, 0}, 4]], Polygon[CirclePoints[{1/2, 0}, {1, 0}, 6]] ][True], Area, NumericalOrder][[1]]
Out[16]=

Output coordinates retain infinite precision:

In[17]:=
First[p1]
Out[17]=

Compare with RegionUnion which does not compute a single polygon:

In[18]:=
non = RegionUnion[Polygon[CirclePoints[{0, 0}, {1, 0}, 4]], Polygon[CirclePoints[{1/2, 0}, {1, 0}, 6]]]
Out[18]=

An explicit result can be approximated using DiscretizeRegion:

In[19]:=
p2 = DiscretizeRegion[non]
Out[19]=

But vertex coordinates are given only to machine precision:

In[20]:=
Short[InputForm[p2]]
Out[20]=

Obtain the intersection of two polygons:

In[21]:=
AbsoluteTiming[ res1 = ReverseSortBy[ResourceFunction["PlanarPolygonFragmentation"][ Polygon[CirclePoints[{0, 0}, {1, 0}, 5]], Polygon[CirclePoints[{1/2, 0}, {1, 0}, 6]] ][True], Area, NumericalOrder][[2]]]
Out[21]=

RegionIntersection is noticeably slower:

In[22]:=
AbsoluteTiming[ res2 = RegionIntersection[Polygon[CirclePoints[{0, 0}, {1, 0}, 5]], Polygon[CirclePoints[{1/2, 0}, {1, 0}, 6]]] ]
Out[22]=

The underlying issue seems to be symbolic swell:

In[23]:=
ByteCount /@ {res1, res2}
Out[23]=

Obtain the remainder of the first polygon after subtracting the second:

In[24]:=
AbsoluteTiming[ First[With[{p1 = Polygon[CirclePoints[{0, 0}, {1, 0}, 4]]}, Select[ResourceFunction["PlanarPolygonFragmentation"][p1, Polygon[CirclePoints[{1/2, 0}, {1, 0}, 6]] ][False], RegionMember[p1, RandomPoint[#]] & ]]] ]
Out[24]=

RegionDifference spends considerable time to obtain a BooleanRegion result:

In[25]:=
AbsoluteTiming[ RegionDifference[Polygon[CirclePoints[{0, 0}, {1, 0}, 5]], Polygon[CirclePoints[{1/2, 0}, {1, 0}, 6]]] ]
Out[25]=

Generate random polygons:

In[26]:=
polys = With[{ rand = SeedRandom[123], vertices = Divide[RandomInteger[{0, 100}, {2, 10, 2}], 100]}, Map[Polygon[#[[Drop[Last[FindShortestTour[#]], -1]]]] &, vertices] ];
In[27]:=
Graphics[{Opacity[.5], EdgeForm[Black], Riffle[{Darker@Green, Lighter@Blue}, polys]}]
Out[27]=

Compute the fragmentation for all possible combinations of circularity:

In[28]:=
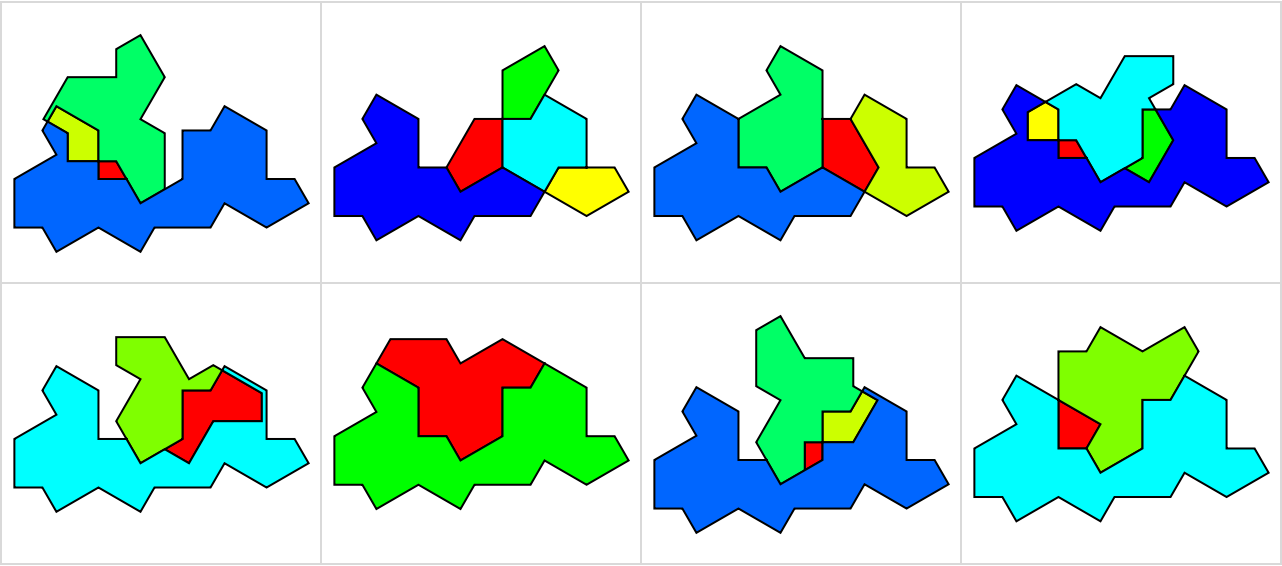
res = Outer[ResourceFunction["PlanarPolygonFragmentation"][ #1 /@ First[polys], #2 /@ Last[polys]] &, {Identity, Reverse}, {Identity, Reverse}, 1];

Verify the invariant transformation property:

In[29]:=
And[ SameQ[res[[1, 1]], res[[2, 2]]], SameQ[res[[1, 2]], res[[2, 1]]] ]
Out[29]=

Verify the covariant transformation property:

In[30]:=
SameQ[ Lookup[res[[1, 1]], {True, False}], Lookup[res[[1, 2]], {False, True}] ]
Out[30]=

Possible Issues (2) 

Self-intersecting polygons will typically not give meaningful results:

In[31]:=
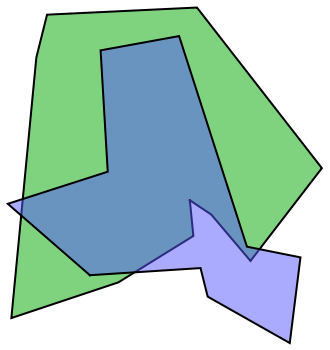
Module[{rand, p1, p2, bg}, rand = SeedRandom["123"]; p1 = Polygon[RandomInteger[30, {5, 2}]/30]; p2 = Polygon[RandomInteger[30, {5, 2}]/30]; bg = Graphics[{EdgeForm[Thick], Opacity[0], EdgeForm[Directive[Thick, Red]], p1, EdgeForm[Directive[Thick, Blue]], p2}]; Map[Show[bg, Graphics[#]] &, ResourceFunction["PlanarPolygonFragmentation"][p1, p2], {2}] ]
Out[31]=

Polygons with holes are not guaranteed to work:

In[32]:=
p1 = Polygon[ CirclePoints[{0, 0}, {2, 0}, 50] -> CirclePoints[{0, 0}, {3/2, 0}, 50]]
Out[32]=
In[33]:=
p2 = Polygon[CirclePoints[{2, 0}, {1, 0}, 50]]
Out[33]=
In[34]:=
res = ResourceFunction["PlanarPolygonFragmentation"][p1, p2]
Out[34]=

Adding seams can allow computation of correct complements::

In[35]:=
p3 = Polygon[ Join[Reverse[CirclePoints[{0, 0}, {2, 0}, 50]], CirclePoints[{0, 0}, {3/2, 0}, 50], {First[CirclePoints[{0, 0}, {3/2, 0}, 50]], First[CirclePoints[{0, 0}, {2, 0}, 50]]}]]
Out[35]=
In[36]:=
With[{res2 = ResourceFunction["PlanarPolygonFragmentation"][p3, p2]}, Show /@ Map[Graphics[{EdgeForm[Thick], Opacity[.1], #}] &, res2, {2}] ]
Out[36]=

The intersection can also be extracted:

In[37]:=
With[{res2 = ResourceFunction["PlanarPolygonFragmentation"][p3, p2]}, Graphics[{Gray, EdgeForm[Thick], Apply[ResourceFunction["PlanarPolygonFragmentation"], res2[False][[1 ;; 2]]][True] }, ImageSize -> 50] // Quiet ]
Out[37]=

Neat Examples (3) 

Combine a pair of hat tiles:

In[38]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/88fd067e-b991-47d2-b67b-3d653e3ced30"]
Out[38]=

Compare options for adding another tile to the fragment:

In[39]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/097b92c9-c639-469b-9d56-2a6b807b2dab"]
Out[39]=

Choose the one valid candidate, and obtain the next largest fragment:

In[40]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/4b6a2395-e3e0-4b65-a88d-deb05835d7d6"]
Out[40]=

Publisher

Brad Klee

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 15 September 2023

Source Metadata

Related Resources

License Information