Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a list of powers of the golden ratio which sum to a given integer
ResourceFunction["PhiNumberSystem"][n] gives the list {x1,x2,…,xk} such that ϕx1 + ϕx2 + … + ϕxk = n, where ϕ is GoldenRatio. |
This gives the golden ratio powers needed to represent 10:
| In[1]:= |
| Out[1]= |
Indeed, the sum of those powers of ϕ is 10:
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= |
Here are the base-ϕ representations of the first 20 natural numbers:
| In[4]:= |
| Out[4]= | 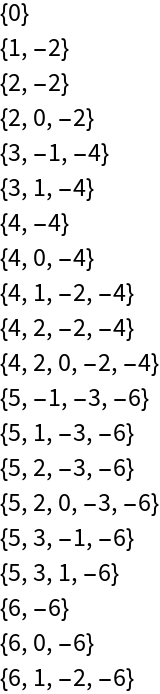 |
A large example:
| In[5]:= |
| Out[5]= |
Check that the corresponding powers of ϕ sum to the original number:
| In[6]:= |
| Out[6]= |
PhiNumberSystem[n] is left unevaluated for n=0:
| In[7]:= |
| Out[7]= |
The sequence of the sums of the lists looks fractal:
| In[8]:= |
| Out[8]= | 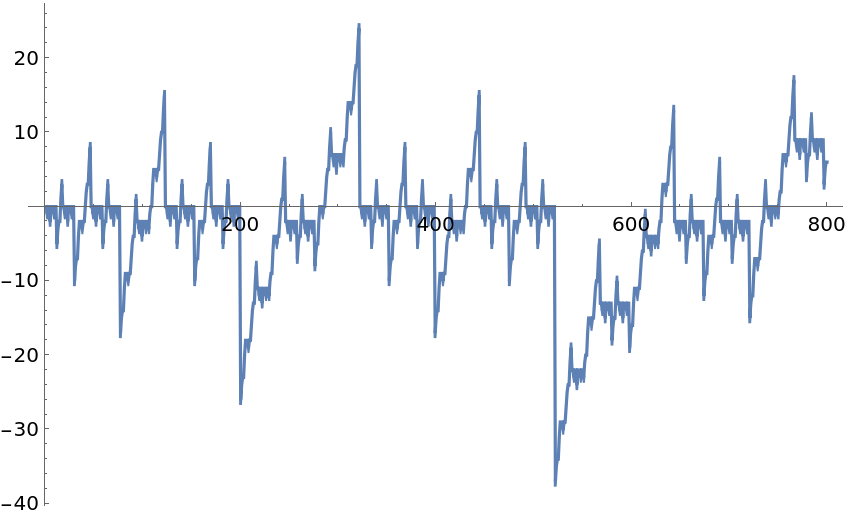 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License