Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PhaseUnwrap

Source Notebook

Remove phase jumps from phase angle data

Contributed by: Sander Huisman

ResourceFunction["PhaseUnwrap"][list]

removes phase jumps in consecutive elements of list by adding ±n 2π for jumps that are larger than the default tolerance of π.

ResourceFunction["PhaseUnwrap"][list,τ]

removes phase jumps in consecutive elements of list by adding ±n τ for jumps that are larger than the default tolerance of τ/2.

ResourceFunction["PhaseUnwrap"][list,τ,tol]

removes phase jumps in consecutive elements of list by adding ±n τ for jumps that are larger than the tolerance tol.

Details

list should be a one-dimensional numerical list.
The default for τ is 2π.
Common settings for τ are 2π and 360 for the use of angles measured in radians and degrees, respectively.
The default tolerance tol is τ/2.
A tolerance tol smaller than τ/2 works effectively the same as a tolerance of τ/2.
ResourceFunction["PhaseUnwrap"] could be seen as the opposite of Mod for a time series as it "unwraps" the "wrapping around" in modular arithmetic.
Possible forms for tol are:
αuses the tolerance α
Scaled[α]uses a tolerance of α τ

Examples

Basic Examples (2) 

Remove the discontinuity in the phase:

In[1]:=
data = CompressedData[" 1:eJwtkl9I01EUx38zxExXWqt8qtY/NKwZ24Ox7FxoWQQGWSjioEhlzdLI3yCI wR4qUhsRjJj2EFiQkyIJIiRo5z5UJEFOm9RoQ8pJRVA+LB9+9/fTgnMe7sPl 3nvu98/Hee5Sc5dN07ST/1eurS984KUBjiB8uv/aAFfnjje3pwzwxDKtji8G tJ/Iz3q/GzCRji+sLxjgL76OCZuCBiMZXFuhYN3ib6tlq4LodMCMuxQMVx8b /ykU+AzfSOCUAndhpnZ/QMG9xFhNd1iBHG6V3piCXOmvntnHCnT53tf7VsGe RUe4cV7Bc3ukc6zIhNF9c1//7DQhU9kRu3bcBD3Sk/+mm5Aqu9LyaMSEAT0f upk2wf0quKHbbkGVx5k832TBrdT2Jwt3LbizeuOuBz8sSKXtDXNHlyG3e9Qb fbEM/eVbXAP1K1C2bb655OMKLDV9GBxs1MSkf1PSPaGJy+MPz9QfsYm6yo5D 2SWbmHG6I+FMkTh74+qFzeYq8fRvXO+9WCzWdD0rHK4tEVV7faeVs1TyXvK5 5PuS30ueJ/tovnxH/0n+X5aTHmR9mCW9yPqR/WCU/CH7RQ/5x37KAzkfDFFe +JnywwTliZwvVlPeGKL8MUt9IPeDQ9QXeqg/5D5xiPpF7hsrqH88SDwg84HM C/qJH2SesI74QuYNs8Qf/gMFcVeS "]; unwrapped = ResourceFunction["PhaseUnwrap"][data]; Column[{ ListPlot[data, Frame -> True, Joined -> False, PlotLabel -> "Original data"], ListPlot[unwrapped, Frame -> True, Joined -> False, PlotLabel -> "Corrected data"] }]
Out[3]=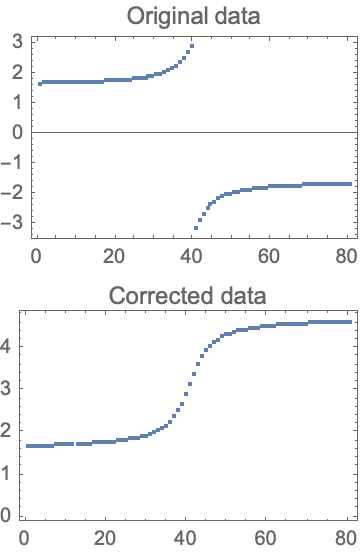

Correct phase jumps in a list of phase angles measured in degrees:

In[4]:=
data = CompressedData[" 1:eJwt0n9EnmEUBuA3TVtKaUspbfnStFKalNJkKU1KqWUpTdYPzUjZjNk0Yzab yGYzplnGlBLZLGM2zZjNMrJZYsoSs2nGlGWkdLXt4frvdh/ncULtvUd7woIg eBf8e1EkECKbQsqooYkOejjPFW4wyDCPeM4bPjDPN1bYYJdBe9hHJvkcpopj nCBcLoYk0smlmArqaKGL0/RxjVvcZ5QnTP3f5xNfWOb39nL6o0ggRDaFlFFD Ex1EiMaRQgZ5lFBJA62c4iyX6OcODxjnKa94zxxL/OQP4fpjSCKdXIqpoI4W uoiUjSeVLAoopZpG2ujmHJcZ4C4PmeAZr5nhM1/5xToR+uNIIYM8Sqikgdaw v18VRJNIGjkUUU4tzXTSywWucpN7jPCYF7zlIwt8Z5VNIg2IJ5UsCiilmkba 2CEXSzL7OcghjlDPcU5yhotc5zZDjDHJS6aZZZEfrG2fgv5oEkkjhyLKqaWZ TnbK7mYvB9gCj2xTwg== "]; unwrapped = ResourceFunction["PhaseUnwrap"][data, 360]; Column[{ ListPlot[data, Sequence[ Frame -> True, PlotLabel -> "Modular data", FrameLabel -> "Degree", ImageSize -> 300]], ListPlot[unwrapped, Sequence[ Frame -> True, PlotLabel -> "Corrected data", FrameLabel -> "Degree", ImageSize -> 300]] }]
Out[6]=

Scope (3) 

Supply a stricter tolerance:

In[7]:=
data = CompressedData[" 1:eJxFlPs/1Ikexr8usxoT5j6jHSWplCl0ppo61eejYitqWaVadkzZlmVE5TAr l1GLo7YTho0IyVbHDrXaZCPmTEKONOpVL3Qb90s4Y91PY+bMb+f5C57n9byf Z/nxyK9OmBAE8ZT4v+Lzl/aePDcP3nkBXdHbybjjikrmnEfHhiH9n3vduBia MRiTd1sLukiLlUPHTXA0f33yiBMZJQ8qJohMGzQvlV8N2ktHXWVkTqgtE5lU xxo/dxaG7hg61P6chbwn91p7OljYkrTMQh/Nwrv/nhgwUzKRe1kSy+xgoJog q73f0nF0PO7i2Y80jKm/xOh0oKHk3YcudQEVdRXu2sFIKmrMo51by6lYe31l ds5xGp4OGilxz6bjd+RxRcROJtIXhjz8vmOjQs5WfTbJRU3IHV91UT8ceb38 3QX/WZDc3eNvvtEUC4Lybvs2L8K5T/6CD4422LAgtqv/kY6ygExJ4OcsFLvQ RsqFHBRW9UaEq7go8ytRe7CVICtfrK/sagBC2pjKPSgDboxLgljFwUCbXwPU chZmp/XXed2io9R7eETJscaCuBNHUhUktO87VWYrmwN7qbOIEqYGZeyI3Ret TAxNTJakXbNG5ahQxys1Q6lpmtv+txOwdAkJQhK5eGt3etKGegauKLvatbTP Gi9ueD14yccCKdEHF450EWjq/VP8f9izkNF9q0V1fgw04X7qKH43aDN3nvA6 0w7KmbGaCnktIDnUqheKgLDc2mS4EAJelk6208ttcSwoid5ha4ub/uZl5zvO xQy52rTgHBd74k9NltdycKuovfqrVDZ2Jy7JdmhjIu+/TeOef6djwsnKKYrI Bj3rXu5alroIuc/sjtGuEChLiZJeqxgH8Z2UKSaHi7NTKTezeumornn/dfCk JVaf3N/a0WsAVJbqg9l9UJGsq9sewMas+CTifhANBWk/Hd18g4zUV8+qIq+a oHilg2Ff2TQU91z/5VRfP8iylxX9i9QCkhdn6jltXBQXWn3z/WkuKl718ko7 jD0N/ONmunsLaFqj9j+T9YG6MdPc78QkyNqpke/36GFRnMVcvpCEu9//2fSm goLHBfxsYoWRo5R7/QeCjPyouuofn+Sg7L5G0eTbDmq3ipp501HIiGmt2jc7 DWiWx/Gw1IFwijYyxiAwOj79gNzZBGsPheftCDRBn/jTfJKKQE0/f12ohQGO VGtEopJP4Jr9oaBXNQvCKDXvomYSMgKTzS7FaqF422rTLRajUPzz12Oy6WG4 m57Z2JjxEXwe1Tk8a9aC00zNS4HHDBS/nl4jj9KDt2dtb1mlOebC3mJSFgVD 13kde9JHw4OPAxI6i9io7aER1/gDkMsjLCfNTDBl9Fp14jorLH947NHOPib6 VDlZf76pG0QbNTxnA4F6rruOc8gKW2tmCtenMZH43tb1h/oWuD3/h0UdaRbw oWeB/SpzbFas9d0opSD97K9XyL9T8TPrDv6bOTpW/TwwSL9s5ILx+8QPySxk PznbUKRhoXZDmNhexcL1/JCkB8BC/5Etu9bGMNFVkyWj/8jAwIjdhitGjgrT y+sdS2j47aPatOVjVHQM15U2naNiSf/6OYaUiv5/abIceEtFno+cf7CGhmsH V8X9lcPAquT8PdRxJjqtONOt3WTsK3XT/PNlzUB0nk0afj8G2tUXBOGVn0DG 377NJcIcBTt4245OW6J23Ks7JNf4Jw65Kw9HMlAaGyb2M/p1fbiXoWzjoOtR Ydlvxl3IdCt2x4mMO28U2rvMK6H5pv2ZoiYuEl1P+WE8Dpayg2+XKZgoMey0 CDhPQwU/8TQpmIKubrc0jvmmKHasU61qmYDFsGAYFnORn9S5tXCajq0fC59v HrbEuYinvBt6A9g/FsSKqvshbw3T5kAXG716Jo66AB2Lk+/Prt6yGEUJF8N+ MSOhMGVRW5ZmASRC+RffkqfAe1tls+/AEFA3v3p9uPMNUPOL7A6XtID4BZPe cP0e4K4cjypKJhCJKZ6qsV0Q9Yee72fMpSGX//M61Rb3Kc43F77gYjOlbfGX XlwUrLlseHmMg2+vhgUmmLBx37tzoXeWMLFIsEGYc4OGRA5b6uJmheLzntlr 5kmocXiQ+2XwJ8iInIl72t8N/wNqIsfY "]; unmod = ResourceFunction["PhaseUnwrap"][data, 2 Pi, 4.5]; ListPlot[unmod, AspectRatio -> 1/4, ImageSize -> 600, PlotMarkers -> Automatic]
Out[9]=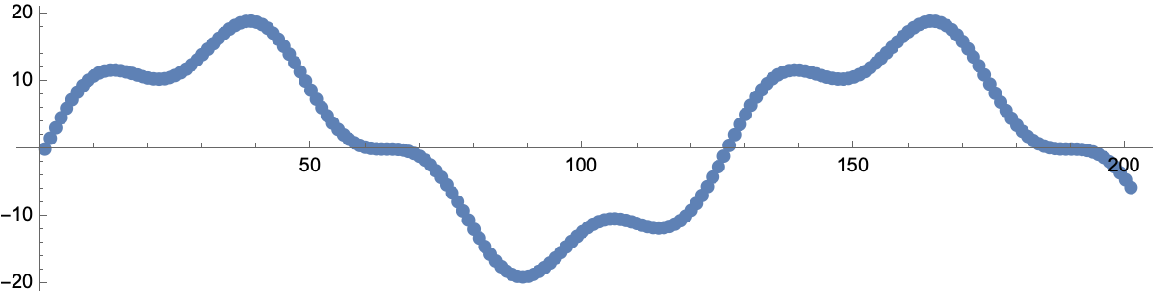

Supply a tolerance as a scaled version of the modulus:

In[10]:=
data = CompressedData[" 1:eJxFlPs/1Ikexr8usxoT5j6jHSWplCl0ppo61eejYitqWaVadkzZlmVE5TAr l1GLo7YTho0IyVbHDrXaZCPmTEKONOpVL3Qb90s4Y91PY+bMb+f5C57n9byf Z/nxyK9OmBAE8ZT4v+Lzl/aePDcP3nkBXdHbybjjikrmnEfHhiH9n3vduBia MRiTd1sLukiLlUPHTXA0f33yiBMZJQ8qJohMGzQvlV8N2ktHXWVkTqgtE5lU xxo/dxaG7hg61P6chbwn91p7OljYkrTMQh/Nwrv/nhgwUzKRe1kSy+xgoJog q73f0nF0PO7i2Y80jKm/xOh0oKHk3YcudQEVdRXu2sFIKmrMo51by6lYe31l ds5xGp4OGilxz6bjd+RxRcROJtIXhjz8vmOjQs5WfTbJRU3IHV91UT8ceb38 3QX/WZDc3eNvvtEUC4Lybvs2L8K5T/6CD4422LAgtqv/kY6ygExJ4OcsFLvQ RsqFHBRW9UaEq7go8ytRe7CVICtfrK/sagBC2pjKPSgDboxLgljFwUCbXwPU chZmp/XXed2io9R7eETJscaCuBNHUhUktO87VWYrmwN7qbOIEqYGZeyI3Ret TAxNTJakXbNG5ahQxys1Q6lpmtv+txOwdAkJQhK5eGt3etKGegauKLvatbTP Gi9ueD14yccCKdEHF450EWjq/VP8f9izkNF9q0V1fgw04X7qKH43aDN3nvA6 0w7KmbGaCnktIDnUqheKgLDc2mS4EAJelk6208ttcSwoid5ha4ub/uZl5zvO xQy52rTgHBd74k9NltdycKuovfqrVDZ2Jy7JdmhjIu+/TeOef6djwsnKKYrI Bj3rXu5alroIuc/sjtGuEChLiZJeqxgH8Z2UKSaHi7NTKTezeumornn/dfCk JVaf3N/a0WsAVJbqg9l9UJGsq9sewMas+CTifhANBWk/Hd18g4zUV8+qIq+a oHilg2Ff2TQU91z/5VRfP8iylxX9i9QCkhdn6jltXBQXWn3z/WkuKl718ko7 jD0N/ONmunsLaFqj9j+T9YG6MdPc78QkyNqpke/36GFRnMVcvpCEu9//2fSm goLHBfxsYoWRo5R7/QeCjPyouuofn+Sg7L5G0eTbDmq3ipp501HIiGmt2jc7 DWiWx/Gw1IFwijYyxiAwOj79gNzZBGsPheftCDRBn/jTfJKKQE0/f12ohQGO VGtEopJP4Jr9oaBXNQvCKDXvomYSMgKTzS7FaqF422rTLRajUPzz12Oy6WG4 m57Z2JjxEXwe1Tk8a9aC00zNS4HHDBS/nl4jj9KDt2dtb1mlOebC3mJSFgVD 13kde9JHw4OPAxI6i9io7aER1/gDkMsjLCfNTDBl9Fp14jorLH947NHOPib6 VDlZf76pG0QbNTxnA4F6rruOc8gKW2tmCtenMZH43tb1h/oWuD3/h0UdaRbw oWeB/SpzbFas9d0opSD97K9XyL9T8TPrDv6bOTpW/TwwSL9s5ILx+8QPySxk PznbUKRhoXZDmNhexcL1/JCkB8BC/5Etu9bGMNFVkyWj/8jAwIjdhitGjgrT y+sdS2j47aPatOVjVHQM15U2naNiSf/6OYaUiv5/abIceEtFno+cf7CGhmsH V8X9lcPAquT8PdRxJjqtONOt3WTsK3XT/PNlzUB0nk0afj8G2tUXBOGVn0DG 377NJcIcBTt4245OW6J23Ks7JNf4Jw65Kw9HMlAaGyb2M/p1fbiXoWzjoOtR Ydlvxl3IdCt2x4mMO28U2rvMK6H5pv2ZoiYuEl1P+WE8Dpayg2+XKZgoMey0 CDhPQwU/8TQpmIKubrc0jvmmKHasU61qmYDFsGAYFnORn9S5tXCajq0fC59v HrbEuYinvBt6A9g/FsSKqvshbw3T5kAXG716Jo66AB2Lk+/Prt6yGEUJF8N+ MSOhMGVRW5ZmASRC+RffkqfAe1tls+/AEFA3v3p9uPMNUPOL7A6XtID4BZPe cP0e4K4cjypKJhCJKZ6qsV0Q9Yee72fMpSGX//M61Rb3Kc43F77gYjOlbfGX XlwUrLlseHmMg2+vhgUmmLBx37tzoXeWMLFIsEGYc4OGRA5b6uJmheLzntlr 5kmocXiQ+2XwJ8iInIl72t8N/wNqIsfY "]; unmod = ResourceFunction["PhaseUnwrap"][data, 2 Pi, Scaled[0.7]]; ListPlot[unmod, AspectRatio -> 1/4, ImageSize -> 600, PlotMarkers -> Automatic]
Out[12]=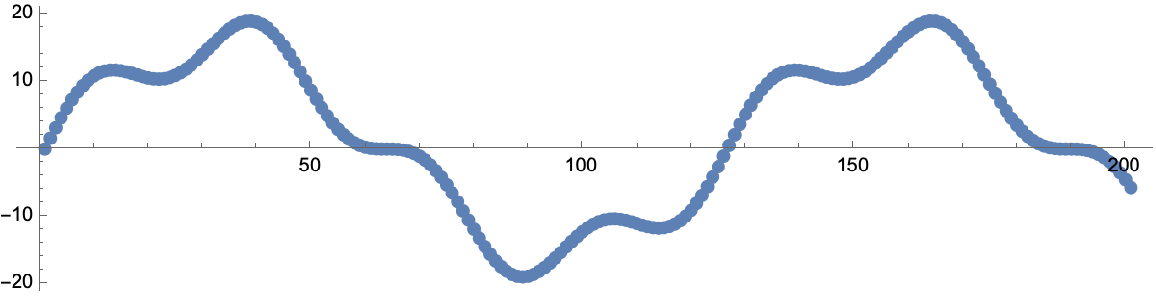

Jumps of multiple times the modulus τ are also removed:

In[13]:=
data = CompressedData[" 1:eJxFkns41Pkex4dcGrOYGWNmOIwoXR66WVuqze+Nilz6fX9MraWM7CobuUTl tBqjXZwKh+j0uGVD2tMRbe1unq01SMS6DG2tZiPXWCsH3Wil8/vvfP77PJ/n +Tzvy8s2LMY/XIfD4bRw/j9JhbKh6FNzlG9+sDZhKxeuFxpUDvlCNI4tzOxc L0VE9uix/G+nqPkYQ/uxMB1MFK5JGV/JRdStqmlOjin0ynMLFDuFmL8Rcz7C QgQRf9ntADdzRLiO7e7qNIfVvZttgz3maE22MVxIMMf1X6afLaoTQfrPqOOi HjNoOFyN7xMhJiZPnP3yTwGOqTPNHtsJENX7VKsp4mO+ym1qNIaPfr0Eh7Zr fNy5ZJ93PkyAI4rxUrc8IQ5wJysPu4sgfDe2PeCAGJW54gaDF1L0H6xmNCUj VOAj294ze95QUde99uh9pIsiRf63zP3FmP1rj/PTZaZofBdqrf5aCFVwTtTe v5kjdK1g/JqLBC4/Dh2ObJBCFVCq2S6uo1TXPli4oW2kOIlNaVK5ipIeW3sy tEGCvab/CdbkmiMvfaTW54oQib5/jNdJTFB0IjwwrVIfS4bjrlqoZqkliQ4h vEMaqu74uLVnmwgRypSo9GIT1E24zFuVL0Kibvp6vyfTlMxSnzqolOLKttPJ TmozLL1aoJUNm+Cs06PRTGIIXoL8XaCWA13fjKT/it9Q2QNXWhu+ek71RwZo Yh0HqKkc93Cf+C6q7vXz21W5dyhwI4yHqBKKY7S5+f2Zg5SP0UqLV7YWeK5I FvZYWGDDUR9rZlKK7FyNbtEpKQaT4l5cuyPB5pCuGv80MQaUlnl2HSJYvW2e 3PEPIU5G33jJCzHFjtoHHjZpiyFtt94vuMCBKjU2sbhqkgqtTn0pkkjx5mVq xbkhITS3+4I+e2GEmmi/tp6h9xTqyhc+Ew9TVSnztVuDxTiXlMz5QSGAc3rG pxvLuOA/bP8xpkAHofZ2772vvqK+Gbx0OW54hFLl2ZTU67dSUd3xakmHFKEX jfd9cUSKyodDVuU9bE/PsipOu7VS/W2xfu2qYUrTlKMXEP6CUnXxY/q8FqjF JwxnC130sa1vpvn3Kh7CnB3zOEtZjlJvjuxSsPw0aNV3oyVomauqsc6kYT/t wU/T0uB2pFKWxgQfc7irDtgTdDn89dWTjwjMxmTV+a4Eva+Pcm1AIFxn4uq3 haCJVvwQtJ6Ab7M8q2kpgcpSVuYlIpjqtXZT6xG4e8TlbJikQR7uM77A/q8p NVpNummkKmO2/dxDw2tN5Lm6KRqLM+ZGGROCM/H++9+vIdivvB/ZHUTg+KzS rT2HwIBWHzr9gODzQFXlZhsG48m7ix3v0hAVv63cu5Ug92yM0b8vEmhvqZCy iMHG3zPP+1fT0BbnHN7A3t+UZ/w6UkIwYViwUP2OoJlJLd2USkP8dcsHcgGB TneGRfQegvPTH6oXsgn6A+yrTtYRmFonNrcOExTor/JYs8Dq6r13U27MQBU4 w/c0YxBCfWepEDCYMbmU4cJl8OvmvpqSeQKn1psfK58T6A9dzGvqJWhJuByq 6GT3iOWrTRsJBsLeZn3xM8HpM6vltXdYX6afHOXdJVjfFf/JjIag1Miv7foz Am+5s4VMj0FYR71d5UoGw9G75vJP0WhYEdD5aoBGZ2NSvcEy1n9qRlZFIIGt 8mzfaAaBLFh97m4tgUKml+40QVDh8Z23O6u3e+NT81VODBpsd60N9GQQtDe/ rEdJY1nc0cD4L2kUVTzh3XJj0Lnp+K1FKxjkt69TG3IYLG+T3TvSTpCX6Yrd bD41D6u3iL0JUlZFKn6ZpbEk9ur3PlsY2DkHzv6LzSszd8WDNFbHaL31pY0s P4d4TmXB9TRa+gpfDdgxkP+002jdY5Yzrwi5wQUCy9kFKmgfwbbaQYXakUDw x/3LYfoEtE5irFkHjbZB3ceOpTTmfjuismJ7a3YP4fkk0DD40/qbwigaQ0qJ JOsQjab0E57+rK/2qO1rPXcwePnISeegO4OJpOP6M5tY31ll8iAHBr3b48bl 5gz0Wp14Y68J/q5eHXGM7ec3EpndxHLkrfHdbxBO8FOicUCrHYGV0I0W3KDx PxGavGQ= "]; unwrapped = ResourceFunction["PhaseUnwrap"][data]; Column[{ ListPlot[data, Sequence[ Frame -> True, Joined -> False, PlotLabel -> "Original data", ImageSize -> 300]], ListPlot[unwrapped, Sequence[ Frame -> True, Joined -> False, PlotLabel -> "Corrected data", ImageSize -> 300]] }]
Out[15]=

Applications (2) 

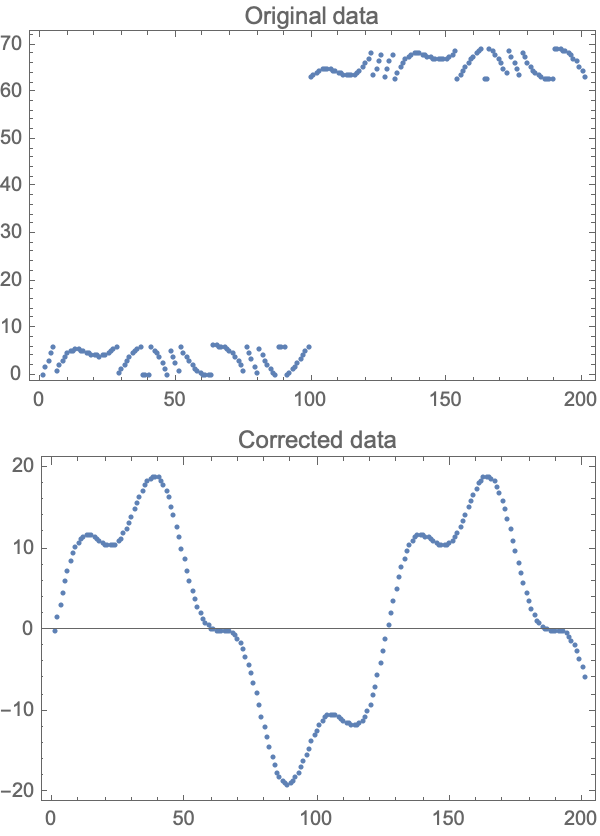Data measured from an angular encoder on a shaft:

In[16]:=
angle = CompressedData[" 1:eJwNlXk81AkYxqeSowOVlY11k2q1lCuhB+M+dpy552fGMGOGuZmiYrWtQiHZ qWxYFaFW7SYKi5ytkFqppSStI1uWbOnQzj/v5/P+9z7v+32eV4/G9WcsI5FI prLSJLC7reUdhXtvjhWd6YqCZUnv5plNVNxbO5h1OpIKvetFBN9E1qukUisK qfA+Nhc/x6JCYzzlh5tPqTBFWip1BQHnnrek98oE+HvsAhQdCLTHmN2i6xAY 73orHOcRGNq1t/kzh8B6qYHmgRoCLss9znoti4bxwyjDqk8E9ks9DzkFR2NV gs2Ob/Kj8bX3O58QQxp64wenp4Jo4EtyScGXaXhXX9RVU0nDB0vVRSGFDvnE 10v5RXR8n3ky72U3HUMfP2xfT8RgqucrIogRgyeP/MdblzNAdPpt93RngMxv 8VX5xEDJgvHA39qx6Nk16nb/ZCyYizVTuzXiULtWzF6UxKHm62cH8xyYcL9/ Lb9jnInpTdeCB75iwab96obCSywY66na5CEe7ZuCB5JV2chYOdM6ZcpGHXOM eL6ZA9F3vToBPRxoUO9trHJOQLp7VfxsawJK1HaV5x5KROHSX6srjbiyeao8 dD9xkVG7LptF4+Gxm8WDVUd5cDNVWJz/zMMZ9vWMNQw+hm4zad71fEgvhXPb DQV4cS7urnqeANO2qcnlMwIsSoYMDgcJ4f5tBne4TAiefK20fasIX16bf3fh igieY88XCHkxdnifb6tNEKNs49G7v06I4dTz70RuYBJIw94dN2c3Io22aHo+ zggk3yPEurmd6Pekbsm1sYXqeYc7wdudoCE3VnaJ6gLdWUltp7YnMi11dd0a fSB6kRCtyPVDv8R8E808AEWX7h7Wfx0IRd9vh3/M2wtR48Pgi3WhqG74iz3T GQ65JLfL00ei8NBN/tRBCwLZVwraTrCi0a6uaR0YQsOx5jcWUT/SUXrN7AV5 hex+vNo9aZMMtCntf6gQFId+4S8bezhMeJxbpCj9zULY4Vq1CWU2yCmsXDdn DtTbNthzkxPwWiS+KF7HxZ5UM8t4Ax4M58yyDwzz0GQeVV+ex0eEoOmKlZsA 1Qdv2zp2CHAj3dXsZKEQEsfp/oxQEWymtVOtPouQ1Xc6/49bYmxl/hHxJC4J zdNKtybe6iFttkXB96kFuhbygsoEgGK9aZd/gSt4NoTX6t99IDWz7LFO8AP5 3EhW5uVADEmHkzMlIcicepy8xTYc3vcDlbZxZL7btfpeyW8EFPceswz6noZX L52HUskxIKnqXxiaY+ABvftsGCcOTxorFf7SYEF+H/dMQ2E8Irx3+8v7c7Dc fyywyCMRN7Iy3QPec3FY65fd6yd5YOyiG+36jQ+1DVZqPrcFWHpSfHPqByFs 9qvs8cgRQTdjJVdiJ4ZW6YLRXTOZrp/DTasvbkZJrOK+P2N3g/SnQkR2Kxk1 DcbkHCMf8I6bE/wxP5jwC42KGoLQH9XYnkEKw2zOKkufI5FYZuuwlnWDgMrn uueKYzQMitUa+O9ioPttvXpIZSw0Ru5myLcwUTB2akWUChuZlRnE2BMO1i6d 6rt6LxE9Vgc7VmbxcL3+Yd0nKR8pypMnJsoF6HXZ73DojhBbxerxciMizOiY 7twt4zftu4HedPeNyOUEzATdt4FJ5aodeu+ckanbt/+Etw96KG05bnsDoNrr 4NX3RQiY6cdfK0ojEE1ftAs6SoAT3pky2yrLF49y8uONDCR5HXG1jYiD3e9y TbcmZH7/XHsn6zkbZ5OdvmA4JiKHobhqwJ+Hc7NKql4FfEjmGuuCawRQz9aS +n4UYk2xfYG8ihju8/nmOjJO0or1H+xsMUdajtIAP8oJNjcnRwe5PqiuGf5H WBaAN9FhAwXxIfiYFZvQeCwS7Ms/uNr4RmOwuFvs8hsdNy0FYVasWEhc/r3G MWah4fWOF51RbMQeHdZ6tCcRmtmrTa/yeHAyOr7hQzEf/607dFtqKIS++pYi ZboIQ3PrK6TdYpCOD5oEVhogbUfZo7F/7JErGPqbI/VCQ6TPm55n/shcpz/B bQgB+c7VZ1pNkYjU8WRdeBAN6yVFM8fwGFTULgpmNOMgeHmkTNk8HkX2JUH2 /3FQl995+Vw7F4Jkuv/SPj7UU1MiuuoEGH7zT1leuAhNuvPFcqVijM5R5hzH 9TC0Mi2k1A+oiVep9rf1Bm8TuTtGNRCjJoEPXE6GQbN775YUfQK1imMm2nZ0 CPq+4VGtYrG1RVh/ScyC74UwEZPJgdlI7qleBy4CawdyDnrwofTc98XMiAAO N5qPkiky3Q1TrsVPZXzMl5c6bzbFpGQybUJKRptYwad5gYLzB1jSn+4EQxLl Il+lFYmmn1z6vjCjIbn6z/5IbQaQ7QD3U0xgyGDb5l/YuDgbNkFdwcVAv8or PVU+dI9vpoQPCtCi53i0iSfCO+oH1X5TmX+2PrP+7LkTNq5ynNkKN9iN/8qJ NfCH5G3kzfZXIXj7oa0+VJtAX81UQF48HVHuhiZ1hnFQtmxXINnFo+PGsOka pUSofLxSFNbIg7a7ahCXJ8DP63gnDmiJ8GbNQvcfs2LobtCJe2hvgcnHo7fG aW6QUIJsl7kGYEjp45yVTxgmIsoq3QUEriRShzutY6BYPPJi8HQcDk+UZm47 yIZa9arYGHcuMmfVVoym8jG3nD/rsE2Il9Y1+vbvRSA9K7/wXl5Hxve4bbqS Myr2Nmwfi6Dg6/Uclr56CKTL2Sk5SVQMNgW0yN+iI3D19R0lwXHQ+vJ053+a bKgnp38zsowLw0g5NY43Hx3XzrA1uUK8P29B9JqI0dxgrjcfoY9cw+vRXnNk VOdVjWw18wdn6ewHSnco9nHuODX3E6hhvJ62IDHQSNZp6pP939lKZfMCuQRs D72voSnzYW3Hq7nfRbL8Dv1uzb8iEUw9JfaPaEkgnuSWqpTLOHufFitZTQFz RS5tXC4EUc3JL5v8CCybMr57JTAGtv32+VoSJkKcWrs2+HEwYGzkZ+XLw0Kk 1KEqSYCK3dbZU1zZPijNr/wrOvaY9VTL17c6YjQ7Lr7wKQWTQ0copZGhOOZz L7lXIRrV2UWJlSEMzPPTRqNFLKRHtS43aErA/+KBOw8= "]; ListPlot[angle]
Out[17]=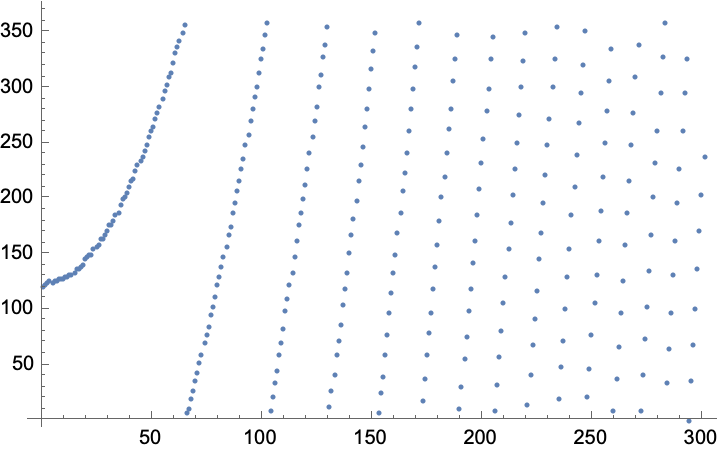

Unwrap data to get the absolute angle of the shaft:

In[18]:=
ListPlot[ResourceFunction["PhaseUnwrap"][angle, 360]]
Out[18]=

Properties and Relations (1) 

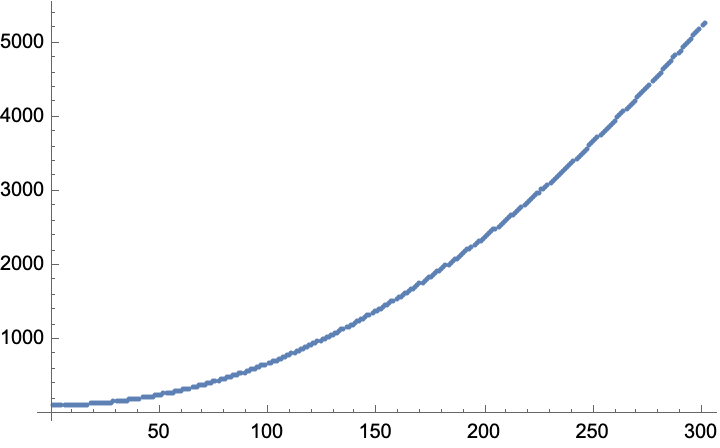PhaseUnwrap is the opposite of Mod for time series of data:

In[19]:=
original = Table[0.3 x, {x, 0, 100}]; modulated = Mod[original, 2 Pi]; unwrapped = ResourceFunction["PhaseUnwrap"][modulated]; original === unwrapped
Out[22]=

Possible Issues (1) 

If the tolerance is too high, steep parts of the function cannot be reconstructed, resulting in partial removal of the discontinuities:

In[23]:=
data = CompressedData[" 1:eJxFzPs/lPkeAPBpmNW4tJqm4bhMhpnncRnMPNaGrZ4PSZdRh8WrHLtRjSZ3 kdYWmrQTlmzquM5Zq6Ricym6LOX51hkvXbRbHUaMXpGEURpeIok557fz/gPe vL1J30Yvo9FoD2j/l6HkDidmz5OB5RH9h9YzYUPpPblLOQtUY0vTW8WWQKxc usoLtIX86X3NN8ftIOdOwjYvjT3IVKferE/jQ+FY3A/11wVgrOubuforBiXc lpxLYhyQJyfsTToOVvNHzZMycTiovlqfIcFB+rniV70OA8vdz0eMMjGYKcFY fL0A6IUvk9pOCmDz7JhHrL0A/BhnLPa/5IPxpN/5qft8+Gw5QA2P8iF29KtD W/wEsCmg9ChXIwDSulz+1TUMVhdztuMqHPZGuZocN3aCEofI8I9HnWFYNtbY ZSoEj3B1zLpGV9D/FNv+Zag7mMxeOV2eJoLFsCMHXQkxxCcEdHT3ikG69yLf KZIAK0OlouwuAT/u7zaunSfA9Rv3EbGBB5z7tJGeoyGANZPwoPg4Afv6Te9O fRDDwXRN+RMfMVjDsc4PISKg8r/X2pxyg3/FnMlbEguhL9ezUVLjBPHfWnjz 5jDADvspIr34cDtYNG54hAc33tVUrSi3Ba4Vg5RlWcIl/7xjBLUKHOoq+rmv V0A+oR49FWQEJodCF3f104AeWJDxnjNHnh669PDeiXfkYFzIk2ThEKkr8ouW pD4l0ey7toazt0lgHjAbJn8jacY+nfqfZSQtishPfvuxXR5WkXciQE4hXUSG dU8tpROlumkn/k3tMnAxU4eqKd3hEo3/i9fUwK2LtH1/n6KmH+mKn+7/RDVP 9DRrR+hIq2yR9t5hooKA69UpanN0wObrGjxwNXpSR28ZEloh72g6XRq1BvGz CjLto+2R77FWH7lAgNhD4eziQRw9po9x/6FwRhEKLItr4Ip6eQaOLtvckUgW nut2UYQy9PBXb5YY3WF9Mb3LmUC1r2YWkmsIlOklk6ZNEkjeQVuMYnig+rUm 259NEIhh+CZu/gKB4pSd7MOeBIpmaHfg1WLUyvYrm5wRoSKCoMUQIrSqIMbU r9MNpToFtaTzXNGEvCA/+IQLUr5K55YuOKF4/AUnodQRLWzNu/VoD44CKmMX V+7DUJNp8NVrVQJk3ET16W0EaOHxOTmnl49qd47XTzzkI8NCnHlkio++O125 Y4WvAJlxDuQ21gvQGZ/Lg5VOGFq5pk43XoOhk8u6m5mrcLTjD54q539/w4nE TdXZOMpka0YnD+AoMext49ByHIU0dP0RGo4h/xTG+7EQAVJYhymDPjgg4oX4 7Y/r7ZG0pLK6zN0ODZQIXWwvWKNWnW+L7DsO6uL6/7Wsyhz9nqB9/wOHga48 yIt4Naujgm44rrD+eojc7Tlo46KnwZKl72eLMDPoaputdMthQ9RHle3c3N8g +3dCHTvMBZsOj6eKCh60341fMk5ygNXdc2n0CT78YlsIcWYYjO5Zzc15joGV 3efzrcE4WMxHFmw/joOhaGe/WQoO1Vd6YvpEONw0oR6xujC4cDJO+0UIBj7b VbVbewQQofnINN8rgA1ptMRCIwFwA6sy9jzjw/d53heNHvNhbZOiMVnPh4r2 OHQpUQC8nz1lShsMZL1JfzKW42B3WWN1WOgIhJHTP49kO8Fl7Tdvx/XOwEnp ad1SJgSv9BCHzevdoGadpDr4pTtsYaWdt7gpAsma3NT/xIshtmVdNotJgKVi pqH+JwKeC5vYsX0EPIppS/Wme8Dus6kvEhcI2ADakyP3CDA9FeppuYsAzwGf UMfbYpCpp+O6p0Sw8dZw0+1P7iCdTyhQ3XeFC1NKIUS4AOuGXV3KXUewVxd2 dplgcOwps1IicQCJf5vZs9N2kNHh7GDUZw3lTuwvd/RzQPJqKtydZEHV8etz uLcp7M7Mj60xYICXYvmfZwYXyXivs5ulzBkycN21+8FvxkjztT3qnX0a0lz5 m+3O8w/JqGdslupcMwkbizfdMCkiaVmKgHvvNpK05WkNY4abKPlah9K68CIq 2cNOZ9/bTJk7qyZzex5SXhuCJGn0AWqwqKv9vcE45UUyGt1tZ6jXQ5uTy+YX KVHHQVEni4GeqH3Zj7eZoigpJxHfykJY5Ajfb4SD/gsugNPz "]; mod = Mod[data, 2 Pi]; unmod = ResourceFunction["PhaseUnwrap"][mod, 2 Pi, 5]; ListPlot[{data, unmod}, AspectRatio -> 1/4, ImageSize -> 600, PlotMarkers -> Automatic]
Out[26]=

Neat Examples (2) 

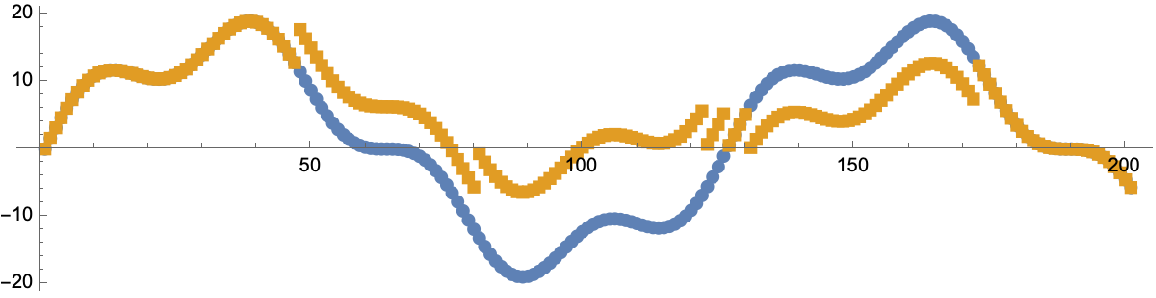Show some modulated data:

In[27]:=
idata = CompressedData[" 1:eJxFlPs/1Ikexr8usxoT5j6jHSWplCl0ppo61eejYitqWaVadkzZlmVE5TAr l1GLo7YTho0IyVbHDrXaZCPmTEKONOpVL3Qb90s4Y91PY+bMb+f5C57n9byf Z/nxyK9OmBAE8ZT4v+Lzl/aePDcP3nkBXdHbybjjikrmnEfHhiH9n3vduBia MRiTd1sLukiLlUPHTXA0f33yiBMZJQ8qJohMGzQvlV8N2ktHXWVkTqgtE5lU xxo/dxaG7hg61P6chbwn91p7OljYkrTMQh/Nwrv/nhgwUzKRe1kSy+xgoJog q73f0nF0PO7i2Y80jKm/xOh0oKHk3YcudQEVdRXu2sFIKmrMo51by6lYe31l ds5xGp4OGilxz6bjd+RxRcROJtIXhjz8vmOjQs5WfTbJRU3IHV91UT8ceb38 3QX/WZDc3eNvvtEUC4Lybvs2L8K5T/6CD4422LAgtqv/kY6ygExJ4OcsFLvQ RsqFHBRW9UaEq7go8ytRe7CVICtfrK/sagBC2pjKPSgDboxLgljFwUCbXwPU chZmp/XXed2io9R7eETJscaCuBNHUhUktO87VWYrmwN7qbOIEqYGZeyI3Ret TAxNTJakXbNG5ahQxys1Q6lpmtv+txOwdAkJQhK5eGt3etKGegauKLvatbTP Gi9ueD14yccCKdEHF450EWjq/VP8f9izkNF9q0V1fgw04X7qKH43aDN3nvA6 0w7KmbGaCnktIDnUqheKgLDc2mS4EAJelk6208ttcSwoid5ha4ub/uZl5zvO xQy52rTgHBd74k9NltdycKuovfqrVDZ2Jy7JdmhjIu+/TeOef6djwsnKKYrI Bj3rXu5alroIuc/sjtGuEChLiZJeqxgH8Z2UKSaHi7NTKTezeumornn/dfCk JVaf3N/a0WsAVJbqg9l9UJGsq9sewMas+CTifhANBWk/Hd18g4zUV8+qIq+a oHilg2Ff2TQU91z/5VRfP8iylxX9i9QCkhdn6jltXBQXWn3z/WkuKl718ko7 jD0N/ONmunsLaFqj9j+T9YG6MdPc78QkyNqpke/36GFRnMVcvpCEu9//2fSm goLHBfxsYoWRo5R7/QeCjPyouuofn+Sg7L5G0eTbDmq3ipp501HIiGmt2jc7 DWiWx/Gw1IFwijYyxiAwOj79gNzZBGsPheftCDRBn/jTfJKKQE0/f12ohQGO VGtEopJP4Jr9oaBXNQvCKDXvomYSMgKTzS7FaqF422rTLRajUPzz12Oy6WG4 m57Z2JjxEXwe1Tk8a9aC00zNS4HHDBS/nl4jj9KDt2dtb1mlOebC3mJSFgVD 13kde9JHw4OPAxI6i9io7aER1/gDkMsjLCfNTDBl9Fp14jorLH947NHOPib6 VDlZf76pG0QbNTxnA4F6rruOc8gKW2tmCtenMZH43tb1h/oWuD3/h0UdaRbw oWeB/SpzbFas9d0opSD97K9XyL9T8TPrDv6bOTpW/TwwSL9s5ILx+8QPySxk PznbUKRhoXZDmNhexcL1/JCkB8BC/5Etu9bGMNFVkyWj/8jAwIjdhitGjgrT y+sdS2j47aPatOVjVHQM15U2naNiSf/6OYaUiv5/abIceEtFno+cf7CGhmsH V8X9lcPAquT8PdRxJjqtONOt3WTsK3XT/PNlzUB0nk0afj8G2tUXBOGVn0DG 377NJcIcBTt4245OW6J23Ks7JNf4Jw65Kw9HMlAaGyb2M/p1fbiXoWzjoOtR Ydlvxl3IdCt2x4mMO28U2rvMK6H5pv2ZoiYuEl1P+WE8Dpayg2+XKZgoMey0 CDhPQwU/8TQpmIKubrc0jvmmKHasU61qmYDFsGAYFnORn9S5tXCajq0fC59v HrbEuYinvBt6A9g/FsSKqvshbw3T5kAXG716Jo66AB2Lk+/Prt6yGEUJF8N+ MSOhMGVRW5ZmASRC+RffkqfAe1tls+/AEFA3v3p9uPMNUPOL7A6XtID4BZPe cP0e4K4cjypKJhCJKZ6qsV0Q9Yee72fMpSGX//M61Rb3Kc43F77gYjOlbfGX XlwUrLlseHmMg2+vhgUmmLBx37tzoXeWMLFIsEGYc4OGRA5b6uJmheLzntlr 5kmocXiQ+2XwJ8iInIl72t8N/wNqIsfY "]; ListPlot[idata, AspectRatio -> 1/4, ImageSize -> 600, PlotMarkers -> Automatic]
Out[28]=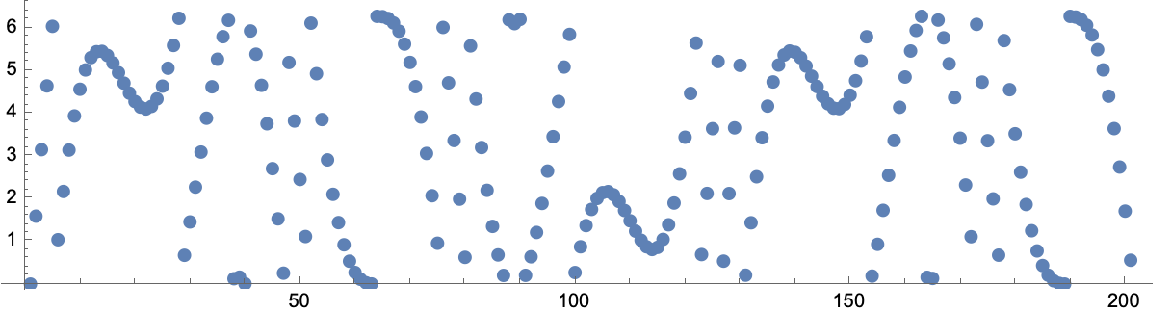

Interactively change the tolerance; for a scaled tolerance of 1, the original signal is returned:

In[29]:=
Manipulate[ ListPlot[ResourceFunction["PhaseUnwrap"][idata, 2 Pi, Scaled[tol]], AspectRatio -> 1/4, ImageSize -> 600, PlotMarkers -> Automatic], {{tol, 1}, 1/2, 1}]
Out[29]=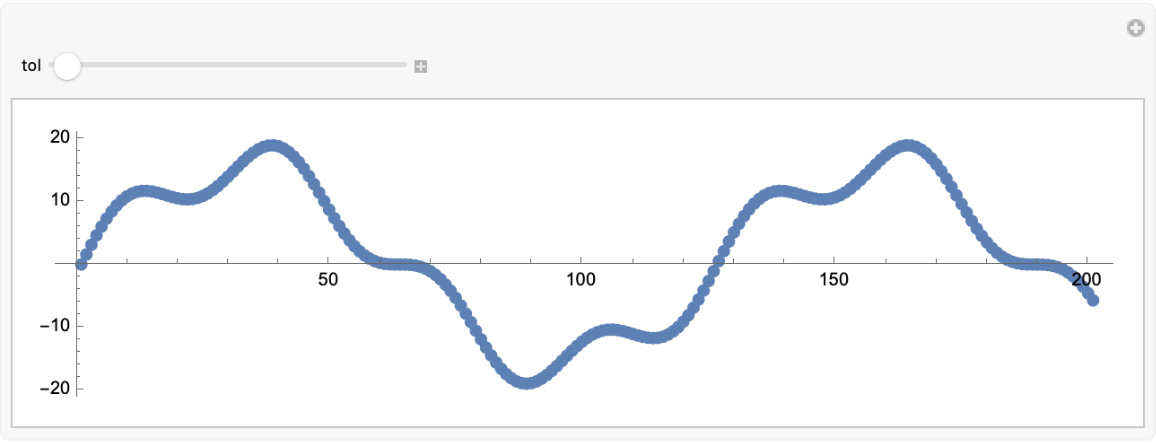

Create some two-dimensional data:

In[30]:=
data = Table[ 2 Sin[0.4 x] + 8 Sin[0.1 x + 0.1 y] + 4 Sin[0.1 y], {x, 0, 100}, {y, 0, 100}]; ListPlot3D[data]
Out[31]=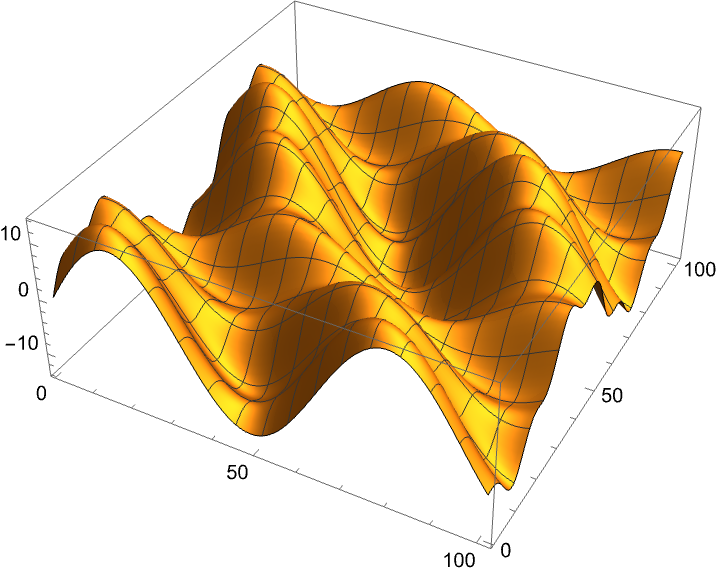

Modulate the data using row-by-row unwrapping:

In[32]:=
mod = Mod[data, 2 Pi]; ListPlot3D[mod]
Out[33]=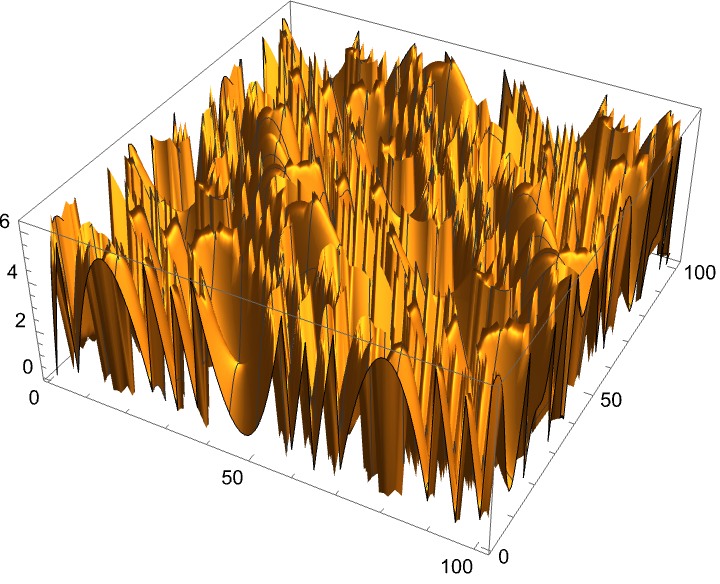

Reconstruct the data:

In[34]:=
unmod = ResourceFunction["PhaseUnwrap"] /@ mod; tmp = ResourceFunction["PhaseUnwrap"][unmod[[All, 1]]] - unmod[[All, 1]]; unmod = unmod + tmp; ListPlot3D[unmod]
Out[37]=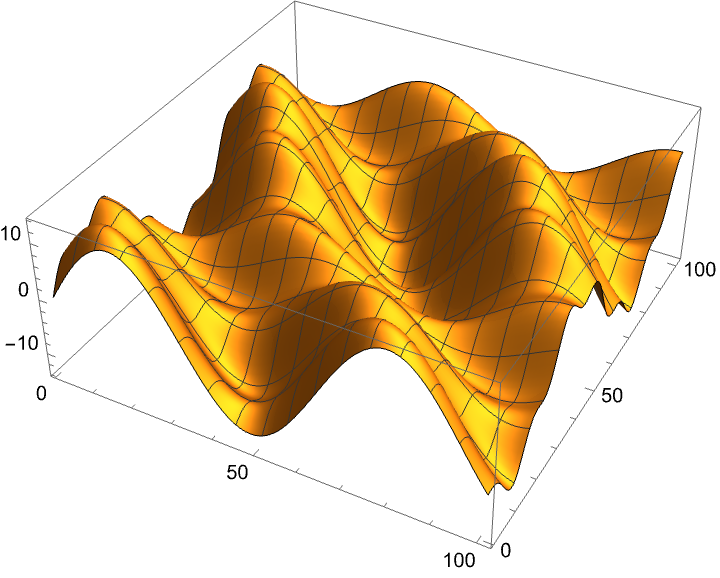

Check that they are the same within machine precision:

In[38]:=
Total[Abs[Chop[unmod - data]], \[Infinity]] === 0
Out[38]=

Publisher

SHuisman

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 30 June 2023
  • 1.0.0 – 20 March 2019

License Information