Details and Options
A Petri net is an abstract mathematical representation of a distributed system (frequently used for describing chemical reactions, biological processes, concurrent computing, etc.) consisting of a directed bipartite graph whose vertices are classified as either "places" or "transitions". The directed edges connecting places and transitions together are known as "arcs".
Each place can contain a number of "tokens", and a given transition will "fire" if the places connected to it by input arcs all contain at least one token. When a transition fires, it redistributes tokens from places connected to it by input arcs to places connected to it by output arcs.
ResourceFunction["PetriNetNondeterministicEvolution"] supports the specification of Petri nets either by
PetriNetObject expressions, a collection of three lists (places
p, transitions
t and arcs
a), or by an explicit association of the form
<|"Places"→p,"Transitions"→t,"Arcs"→a|>. The list of arcs
a should be a list of either rules or
DirectedEdge objects (each connecting a place to a transition, or vice versa).
PetriNetObject expressions can be constructed using the MakePetriNet resource function.
When specifying Petri nets in terms of lists or associations, the list init should be a list of integers specifying how many initial tokens to assign to each place. If a list init is not given, ResourceFunction["PetriNetNondeterministicEvolution"] will assume that each place contains no tokens.
ResourceFunction["PetriNetNondeterministicEvolution"] evolves the specified Petri net nondeterministically by randomly selecting and applying one possible transition firing at each step.
When no step count n is specified, ResourceFunction["PetriNetNondeterministicEvolution"] will evolve the Petri net nondeterministically for a single step and return a single result. When a step count n is specified, ResourceFunction["PetriNetNondeterministicEvolution"] will evolve the Petri net nondeterministically for n steps and return a list of the intermediate results at each step.
When no property prop is specified, ResourceFunction["PetriNetNondeterministicEvolution"] will assume the "PetriNetObjects" property (i.e. it will return a list of the PetriNetObject expressions obtained during the evolution).
In ResourceFunction["PetriNetNondeterministicEvolution"][…,"prop"], the following properties can be requested:
| "PetriNetObjects" | list of PetriNetObject expressions obtained |
| "LabeledGraphs" | list of directed graph representations obtained (with token counts represented graphically) |
| "LabeledGraphsHighlighted" | list of directed graph representations obtained (with token counts represented graphically), and with transition firings highlighted |
| "WeightedGraphs" | list of directed graph representations obtained (with token counts represented as vertex weights) |
| "WeightedGraphsHighlighted" | list of directed graph representations obtained (with token counts represented as vertex weights), and with transition firings highlighted |
| "Tokens" | list of token numbers associated to each place after each firing |
| "TokenFirings" | list of token numbers associated to each place after each firing, with the corresponding transition firing specified |
ResourceFunction["PetriNetNondeterministicEvolution"] accepts the same options as
Graph.
In a PetriNetObject expression, the following properties are supported:
| "AssociationForm" | Petri net represented as an association of places, transitions and arcs |
| "Places" | list of places in the Petri net |
| "PlaceCount" | number of places in the Petri net |
| "Transitions" | list of transitions in the Petri net |
| "TransitionCount" | number of transitions in the Petri net |
| "Arcs" | list of arcs in the Petri net |
| "ArcCount" | number of arcs in the Petri net |
| "Tokens" | list of token numbers associated to each place in the Petri net |
| "TokenCount" | total number of tokens across all places in the Petri net |
| "UnlabeledGraph" | directed graph form of the Petri net without token counts represented graphically |
| "LabeledGraph" | directed graph form of the Petri net with token counts represented graphically |
| "WeightedGraph" | directed graph form of the Petri net with token counts represented as vertex weights |
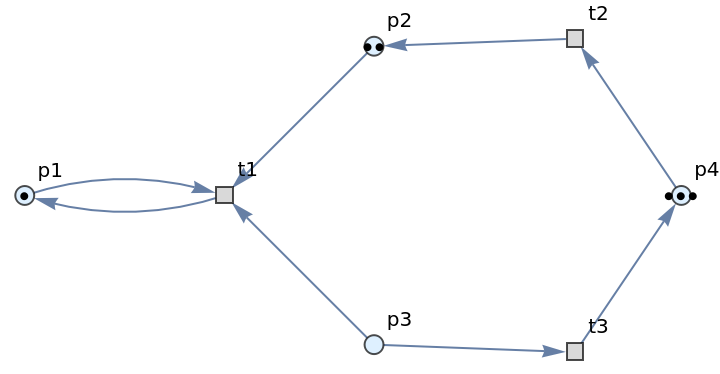
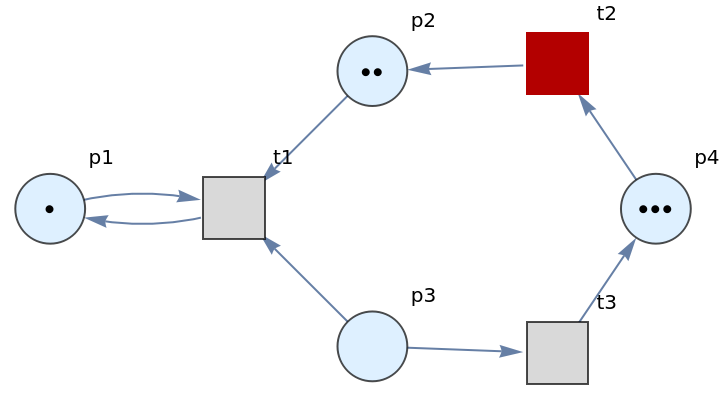
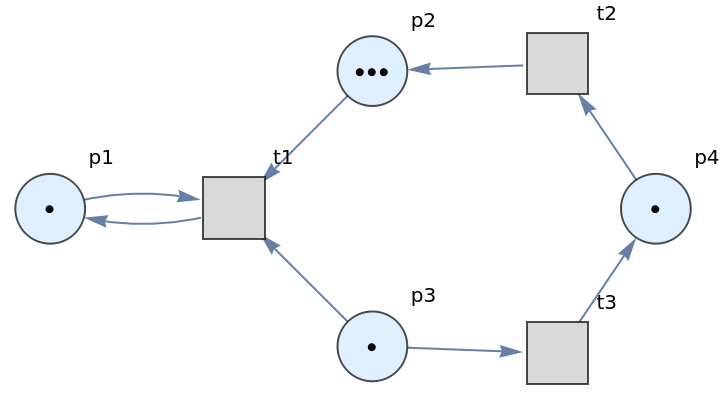
By convention, ResourceFunction["PetriNetNondeterministicEvolution"] renders places as circles, transitions as squares, arcs as directed edges and tokens as black dots.

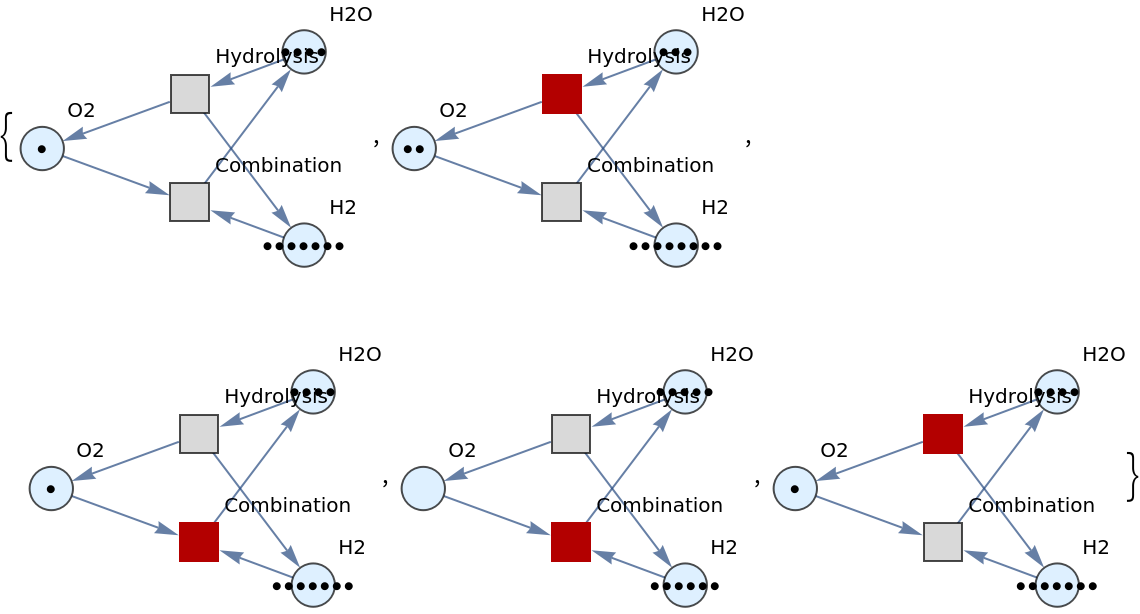
![ResourceFunction[
"PetriNetNondeterministicEvolution"][<|
"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 4]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/0edec28134444d6e.png)

![ResourceFunction[
"PetriNetNondeterministicEvolution"][<|
"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 4, "Tokens"]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/526528dcc57b66ad.png)
![ResourceFunction[
"PetriNetNondeterministicEvolution"][<|
"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 4, "TokenFirings"]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/3a219594cb22405a.png)
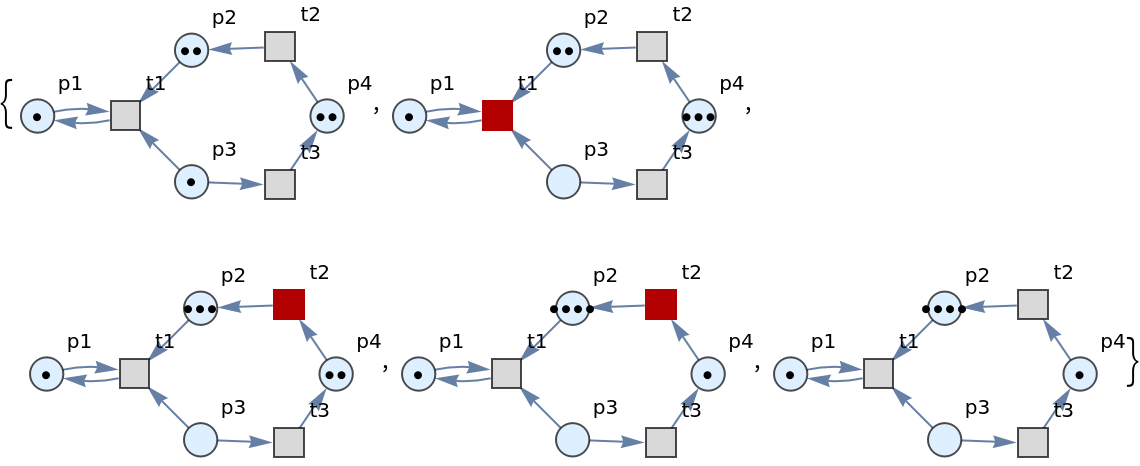
![ResourceFunction[
"PetriNetNondeterministicEvolution"][<|
"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 4, "LabeledGraphsHighlighted"]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/0990114ec66d3d27.png)
![ResourceFunction[
"PetriNetNondeterministicEvolution"][<|
"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 4, "WeightedGraphsHighlighted", VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/0cb62bccb4ab4a85.png)
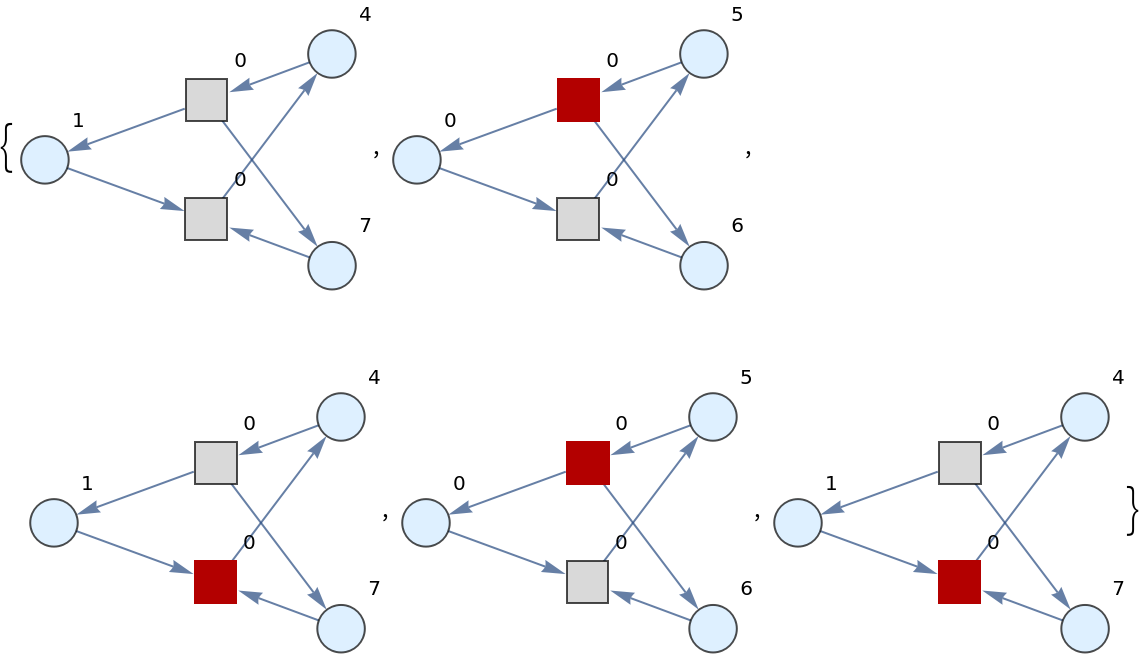
![ResourceFunction[
"PetriNetNondeterministicEvolution"][<|
"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 4, "WeightedGraphs", VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/0801e5c27bd229ba.png)
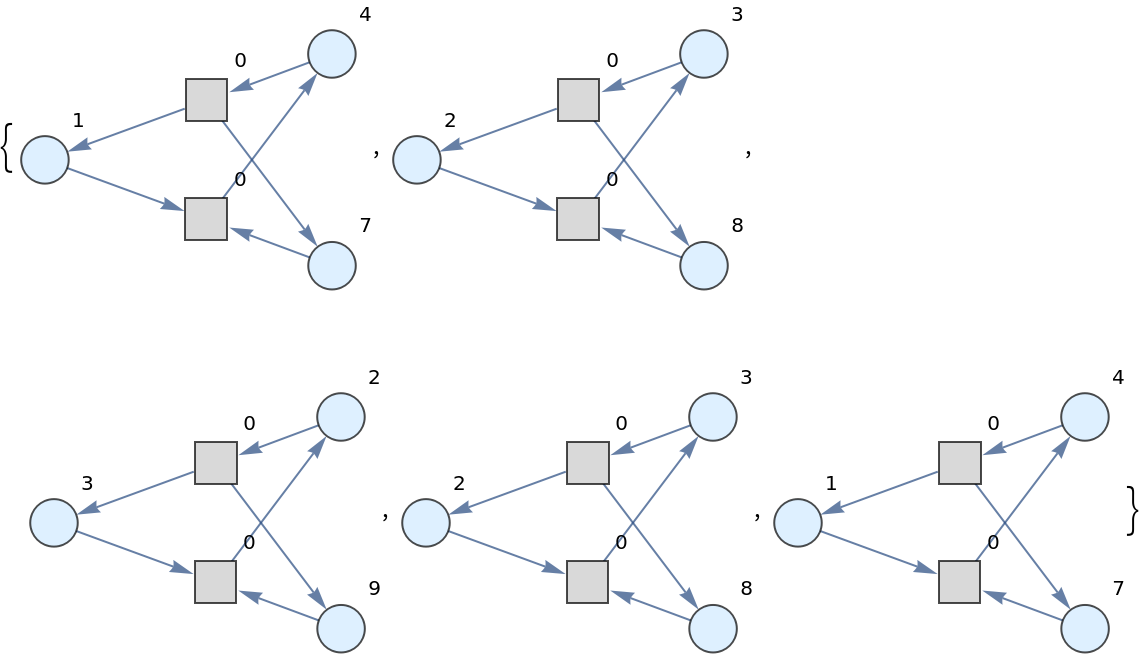
![ResourceFunction[
"PetriNetNondeterministicEvolution"][{p1, p2, p3, p4, p5, p6, p7, p8}, {"Person 1", "Person 2", "Send Message", "Receive Message", "Receive Acknowledgement", "Send Acknowledgement"}, {"Person 1" -> p1, p1 -> "Send Message", "Send Message" -> p3, "Send Message" -> p4, p3 -> "Receive Message",
p4 -> "Receive Acknowledgement", "Receive Acknowledgement" -> p7, p7 -> "Person 1", "Receive Message" -> p5, p5 -> "Send Acknowledgement", "Send Acknowledgement" -> p6, "Send Acknowledgement" -> p8, p8 -> "Person 2", "Person 2" -> p2, p2 -> "Receive Message", p6 -> "Receive Acknowledgement"}, {0, 2, 0,
6, 1, 1, 2, 1}, 4]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/09a23d6c9cdd3615.png)
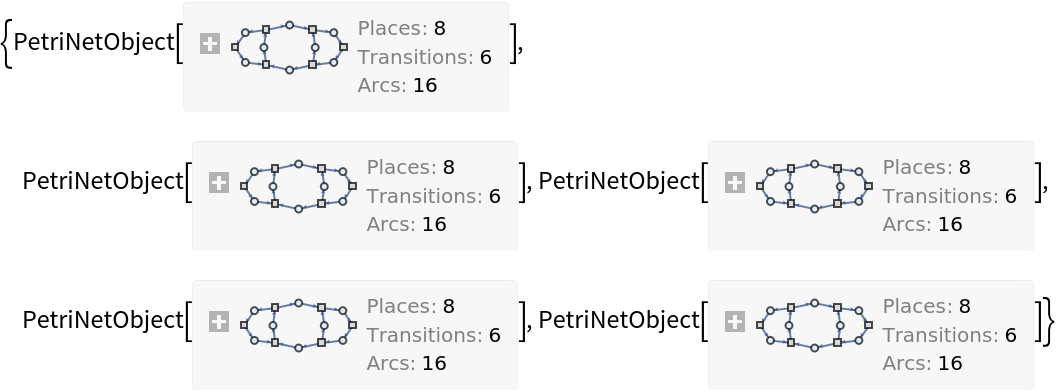
![ResourceFunction[
"PetriNetNondeterministicEvolution"][{p1, p2, p3, p4, p5, p6, p7, p8}, {"Person 1", "Person 2", "Send Message", "Receive Message", "Receive Acknowledgement", "Send Acknowledgement"}, {"Person 1" -> p1, p1 -> "Send Message", "Send Message" -> p3, "Send Message" -> p4, p3 -> "Receive Message",
p4 -> "Receive Acknowledgement", "Receive Acknowledgement" -> p7, p7 -> "Person 1", "Receive Message" -> p5, p5 -> "Send Acknowledgement", "Send Acknowledgement" -> p6, "Send Acknowledgement" -> p8, p8 -> "Person 2", "Person 2" -> p2, p2 -> "Receive Message", p6 -> "Receive Acknowledgement"}, {0, 2, 0,
6, 1, 1, 2, 1}, 4, "TokenFirings"]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/156766c24b334d80.png)
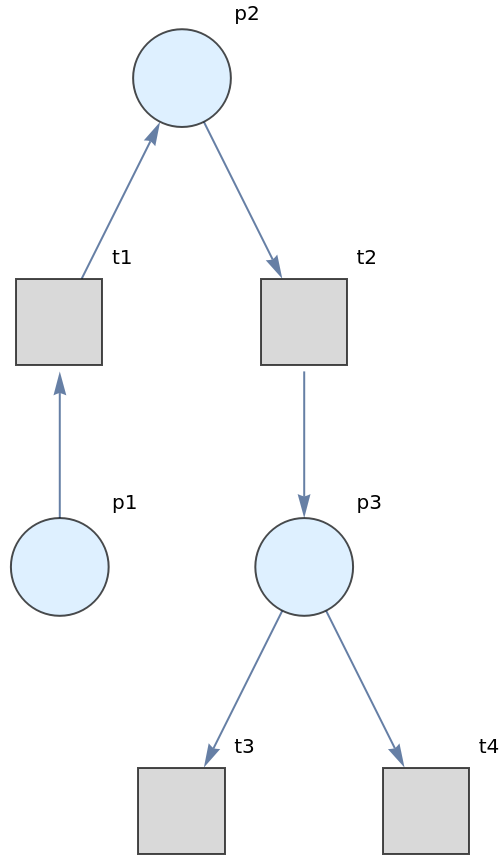
![petriNet = ResourceFunction["MakePetriNet"][{p1, p2, p3, "Buffer", p4}, {"Produce", t1, t2, "Consume"}, {p1 -> "Produce", "Produce" -> p3, p3 -> t2, t2 -> p1, t2 -> "Buffer", "Buffer" -> t1, t1 -> p4, p4 -> "Consume", "Consume" -> p2, p2 -> t1}, {1, 3, 0, 6, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/4c326c89e72ac1a0.png)

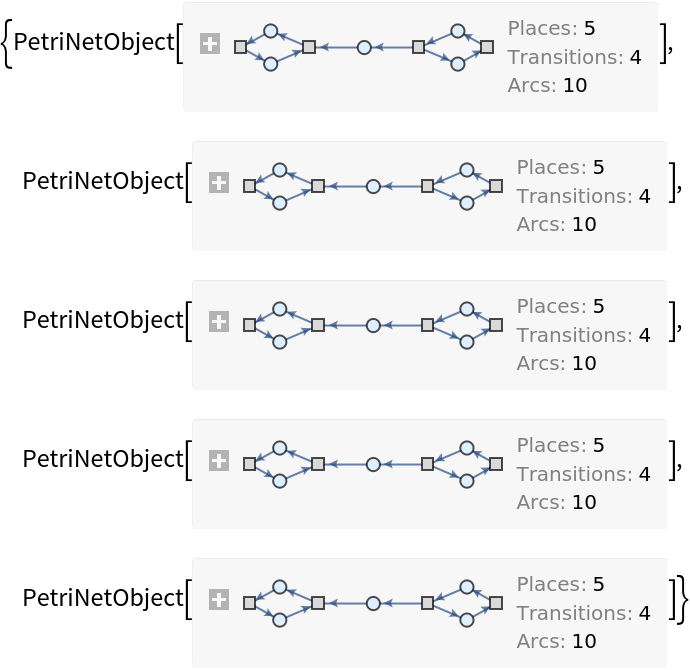




![ResourceFunction[
"PetriNetNondeterministicEvolution"][{p1, p2, p3, p4}, {t1, t2, t3}, {p1 -> t1, t1 -> p1, p2 -> t1, p3 -> t1, t2 -> p2, p3 -> t3, t3 -> p4, p4 -> t2}, {1, 2, 1, 2}, "LabeledGraphs"]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/25188b64d2414f52.png)
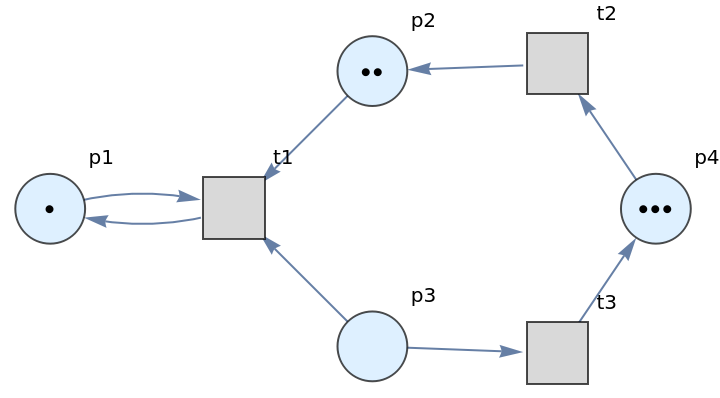
![ResourceFunction[
"PetriNetNondeterministicEvolution"][{p1, p2, p3, p4}, {t1, t2, t3}, {p1 -> t1, t1 -> p1, p2 -> t1, p3 -> t1, t2 -> p2, p3 -> t3, t3 -> p4, p4 -> t2}, {1, 2, 1, 2}, "LabeledGraphs", VertexSize -> 0.1]](https://www.wolframcloud.com/obj/resourcesystem/images/a1d/a1d43ab8-bca3-45f2-85a1-c5e2d0070f67/0bbf0b1765f8dcd5.png)