Details and Options
A Petri net is an abstract mathematical representation of a distributed system (frequently used for describing chemical reactions, biological processes, concurrent computing, etc.) consisting of a directed bipartite graph whose vertices are classified as either "places" or "transitions". The directed edges connecting places and transitions together are known as "arcs".
Each place can contain a number of "tokens", and a given transition will "fire" if the places connected to it by input arcs all contain at least one token. When a transition fires, it redistributes tokens from places connected to it by input arcs to places connected to it by output arcs.
ResourceFunction["PetriNetMultiwayEvolution"] supports the specification of Petri nets either by
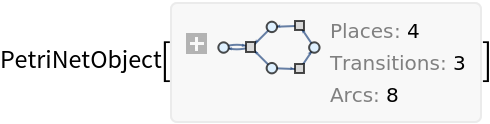
PetriNetObject expressions, a collection of three lists (places
p, transitions
t and arcs
a), or by an explicit association of the form
<|"Places"→p,"Transitions"→t,"Arcs"→a|>. The list of arcs
a should be a list of either rules or
DirectedEdge objects (each connecting a place to a transition, or vice versa).
PetriNetObject expressions can be constructed using the
MakePetriNet resource function.
When specifying Petri nets in terms of lists or associations, the list init should be a list of integers specifying how many initial tokens to assign to each place. If a list init is not given, ResourceFunction["PetriNetMultiwayEvolution"] will assume that each place contains no tokens.
ResourceFunction["PetriNetMultiwayEvolution"] evolves the specified Petri net by applying all possible transition firings at each step.
When no step count n is specified, ResourceFunction["PetriNetMultiwayEvolution"] will evolve the Petri net for a single step and return a list of all possible results. When a step count n is specified, ResourceFunction["PetriNetMultiwayEvolution"] will evolve the Petri net for n steps and return a nested list containing all possible results at each step.
When no property prop is specified, ResourceFunction["PetriNetMultiwayEvolution"] will assume the "PetriNetObjects" property (i.e. it will return a list of the PetriNetObject expressions obtained during the evolution).
In ResourceFunction["PetriNetMultiwayEvolution"][…,"prop"], the following properties can be requested:
| "PetriNetObjects" | list of PetriNetObject expressions obtained |
| "LabeledGraphs" | list of directed graph representations obtained (with token counts represented graphically) |
| "LabeledGraphsHighlighted" | list of directed graph representations obtained (with token counts represented graphically), and with transition firings highlighted |
| "WeightedGraphs" | list of directed graph representations obtained (with token counts represented as vertex weights) |
| "WeightedGraphsHighlighted" | list of directed graph representations obtained (with token counts represented as vertex weights), and with transition firings highlighted |
| "Tokens" | list of token numbers associated to each place after each firing |
| "TokenFirings" | list of token numbers associated to each place after each firing, with the corresponding transition firing specified |
ResourceFunction["PetriNetMultiwayEvolution"] accepts the same options as
Graph.
In a PetriNetObject expression, the following properties are supported:
| "AssociationForm" | Petri net represented as an association of places, transitions and arcs |
| "Places" | list of places in the Petri net |
| "PlaceCount" | number of places in the Petri net |
| "Transitions" | list of transitions in the Petri net |
| "TransitionCount" | number of transitions in the Petri net |
| "Arcs" | list of arcs in the Petri net |
| "ArcCount" | number of arcs in the Petri net |
| "Tokens" | list of token numbers associated to each place in the Petri net |
| "TokenCount" | total number of tokens across all places in the Petri net |
| "UnlabeledGraph" | directed graph form of the Petri net without token counts represented graphically |
| "LabeledGraph" | directed graph form of the Petri net with token counts represented graphically |
| "WeightedGraph" | directed graph form of the Petri net with token counts represented as vertex weights |
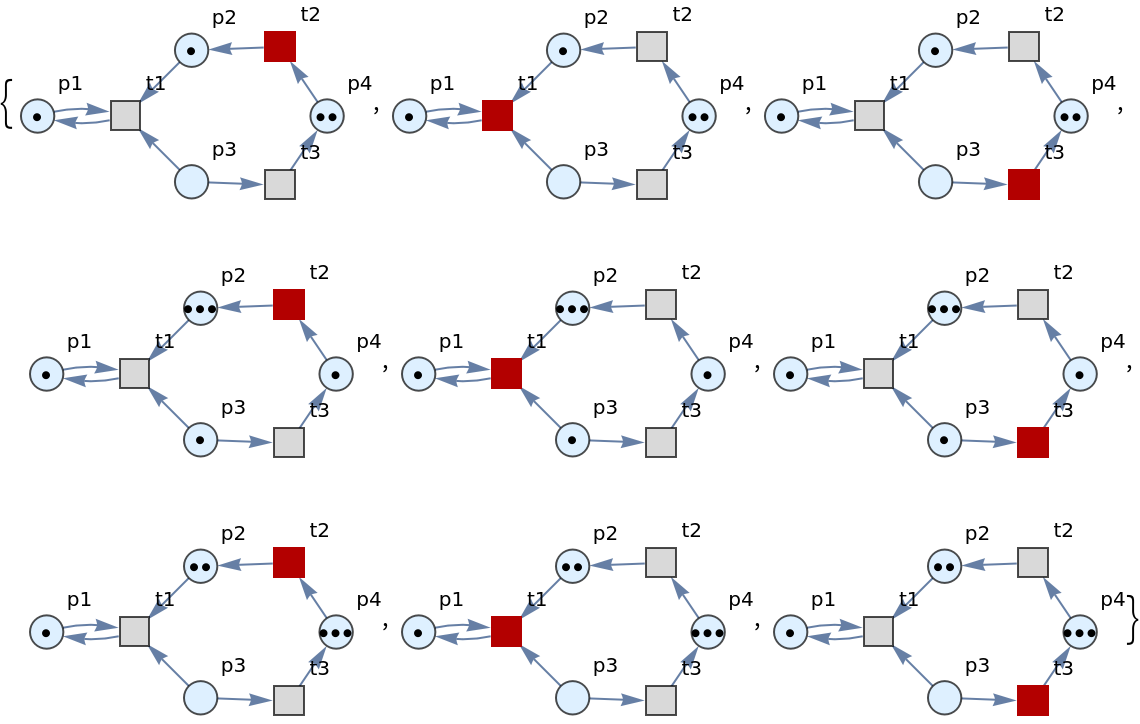
By convention, ResourceFunction["PetriNetMultiwayEvolution"] renders places as circles, transitions as squares, arcs as directed edges and tokens as black dots.

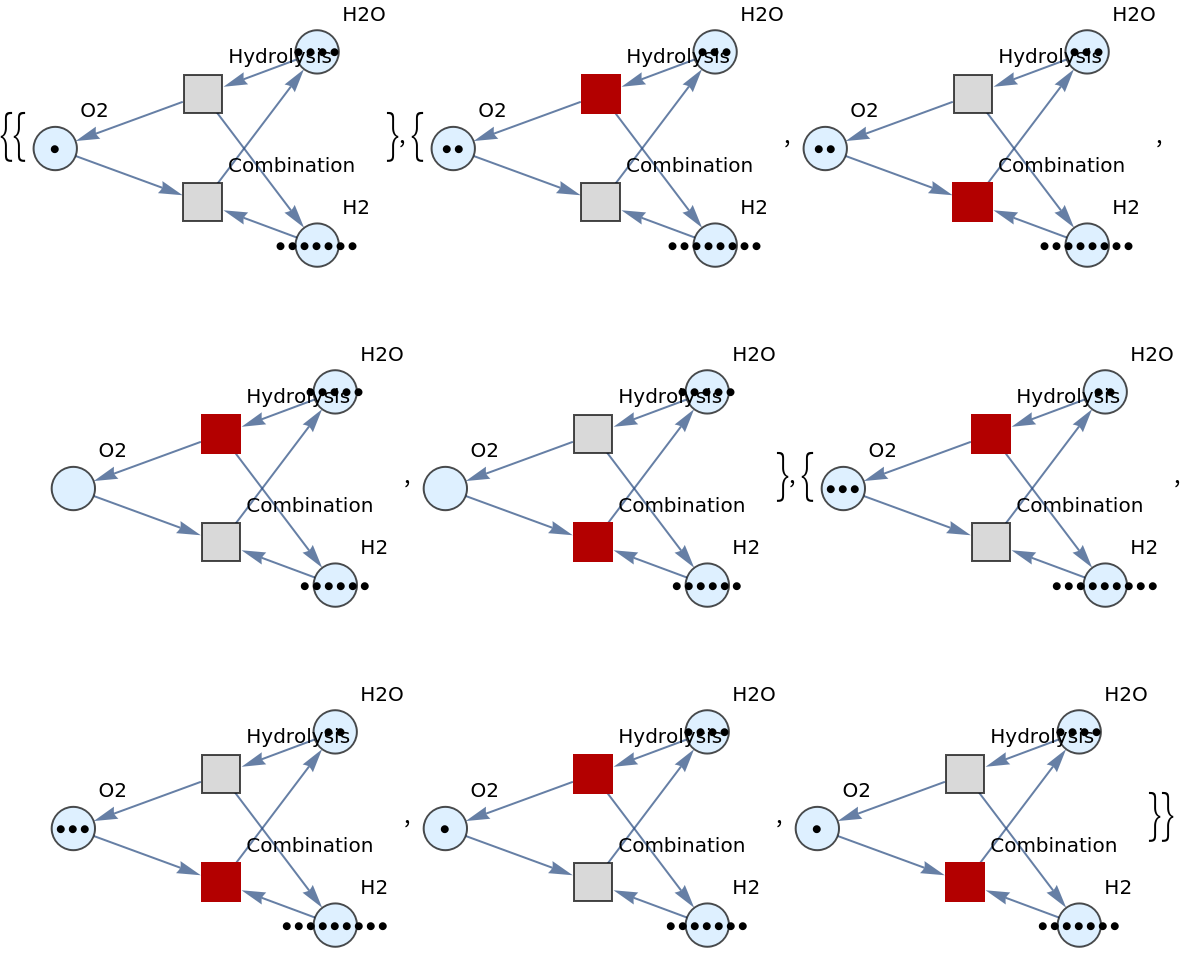
![ResourceFunction[
"PetriNetMultiwayEvolution"][<|"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 3]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/2ee6a5b2f1f2cc89.png)
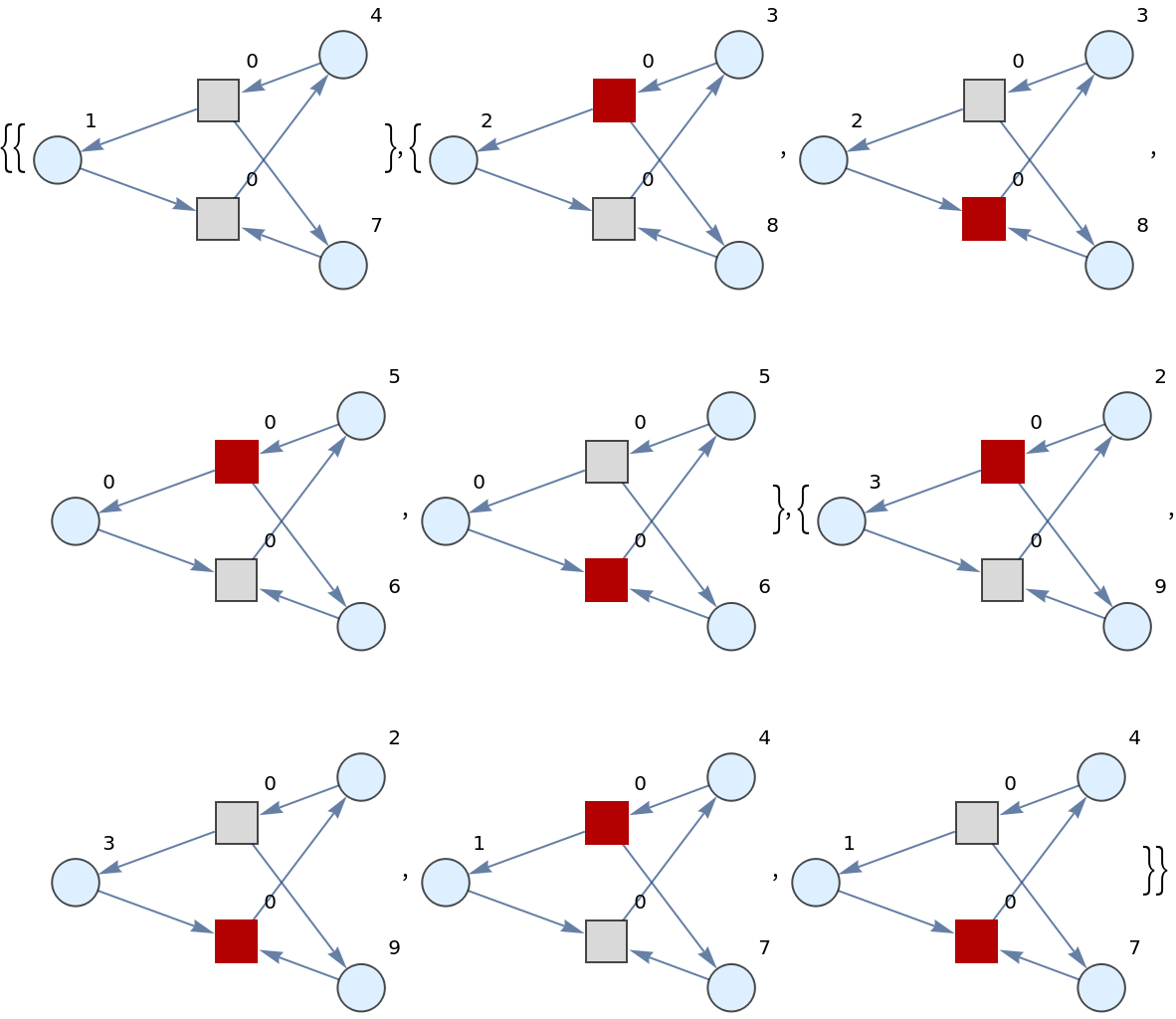
![ResourceFunction[
"PetriNetMultiwayEvolution"][<|"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 3, "Tokens"]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/24e36affdea63ece.png)
![ResourceFunction[
"PetriNetMultiwayEvolution"][<|"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combiantion"}|>, {1, 4, 7}, 3, "TokenFirings"]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/75d7adc35eca3015.png)

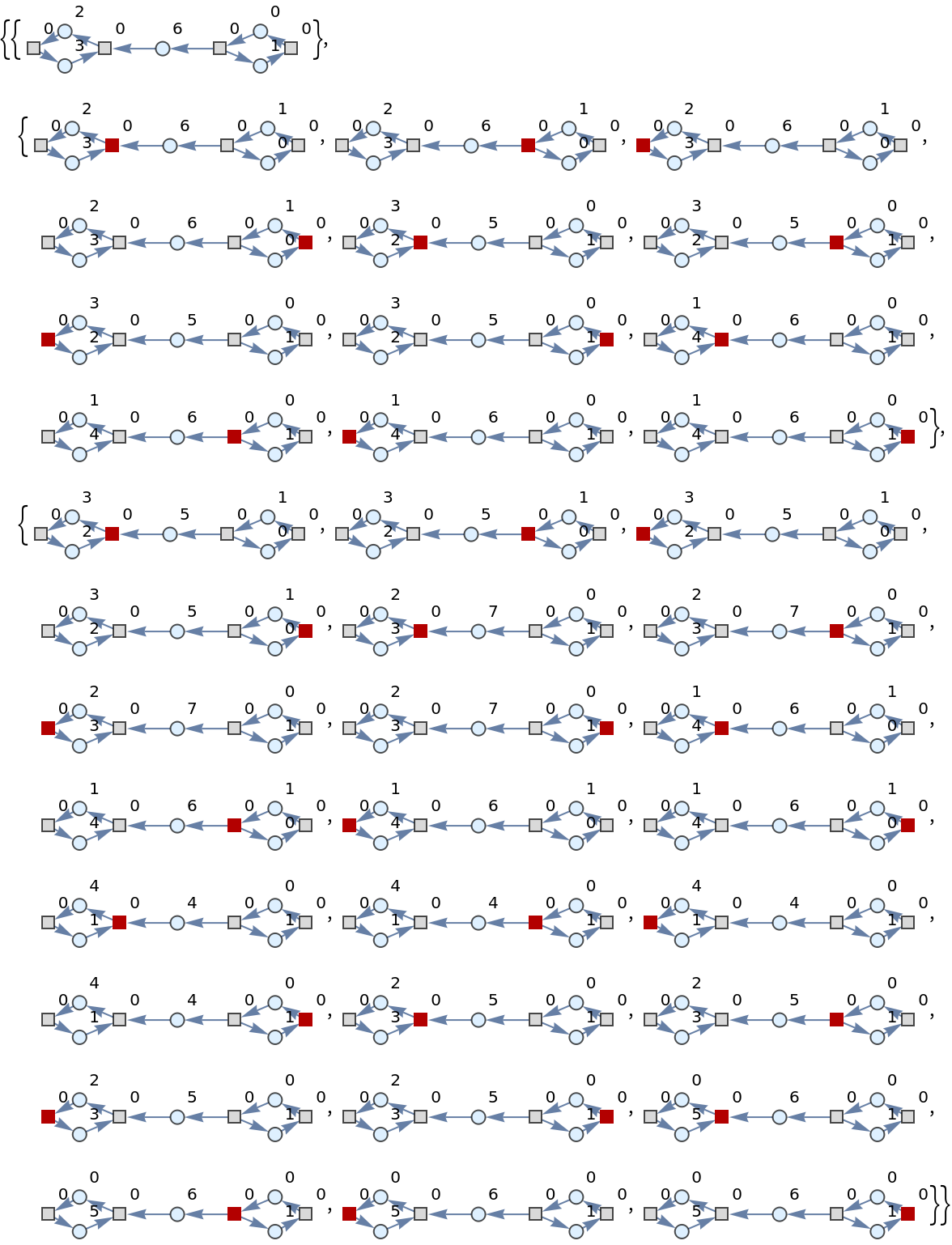
![ResourceFunction[
"PetriNetMultiwayEvolution"][<|"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 2, "LabeledGraphsHighlighted"]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/719cf9597807b173.png)
![ResourceFunction[
"PetriNetMultiwayEvolution"][<|"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 2, "WeightedGraphsHighlighted", VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/02b3950d8a0c3bce.png)
![ResourceFunction[
"PetriNetMultiwayEvolution"][<|"Places" -> {"O2", "H2O", "H2"}, "Transitions" -> {"Hydrolysis", "Combination"}, "Arcs" -> {"Hydrolysis" -> "O2", "O2" -> "Combination", "Combination" -> "H2O", "H2O" -> "Hydrolysis", "Hydrolysis" -> "H2", "H2" -> "Combination"}|>, {1, 4, 7}, 2, "WeightedGraphs", VertexLabels -> "VertexWeight"]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/46b5996a0ec01690.png)
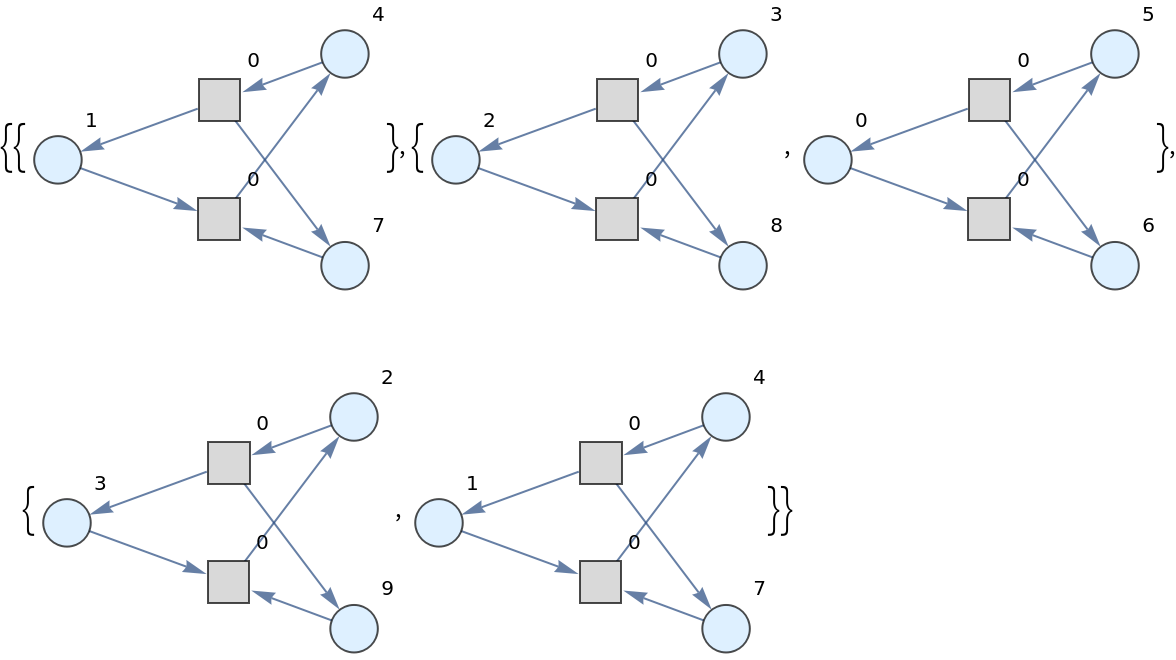
![ResourceFunction[
"PetriNetMultiwayEvolution"][{p1, p2, p3, p4, p5, p6, p7, p8}, {"Person 1", "Person 2", "Send Message", "Receive Message", "Receive Acknowledgement", "Send Acknowledgement"}, {"Person 1" -> p1, p1 -> "Send Message", "Send Message" -> p3, "Send Message" -> p4, p3 -> "Receive Message",
p4 -> "Receive Acknowledgement", "Receive Acknowledgement" -> p7, p7 -> "Person 1", "Receive Message" -> p5, p5 -> "Send Acknowledgement", "Send Acknowledgement" -> p6, "Send Acknowledgement" -> p8, p8 -> "Person 2", "Person 2" -> p2, p2 -> "Receive Message", p6 -> "Receive Acknowledgement"}, {0, 2, 0,
6, 1, 1, 2, 1}, 2]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/498737e65b894f01.png)
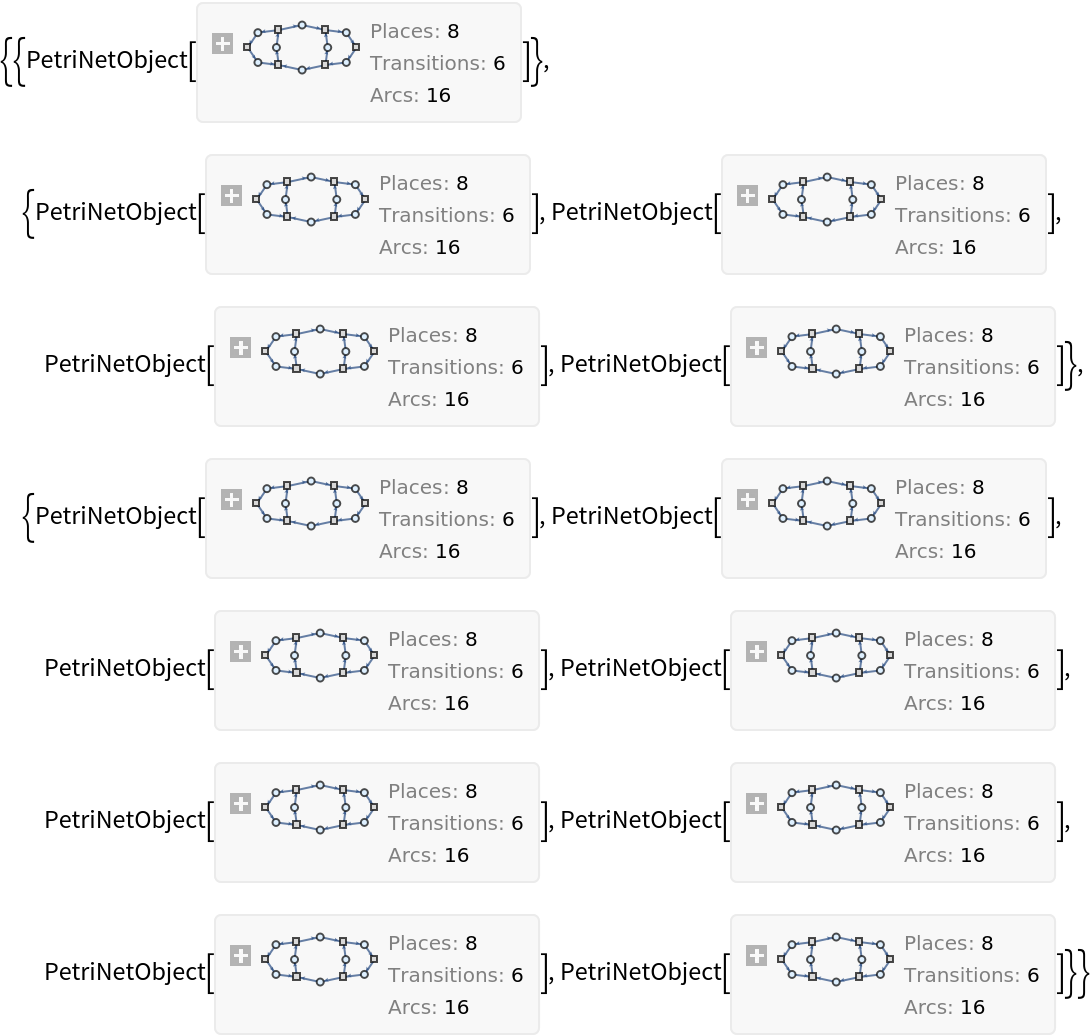
![ResourceFunction[
"PetriNetMultiwayEvolution"][{p1, p2, p3, p4, p5, p6, p7, p8}, {"Person 1", "Person 2", "Send Message", "Receive Message", "Receive Acknowledgement", "Send Acknowledgement"}, {"Person 1" -> p1, p1 -> "Send Message", "Send Message" -> p3, "Send Message" -> p4, p3 -> "Receive Message",
p4 -> "Receive Acknowledgement", "Receive Acknowledgement" -> p7, p7 -> "Person 1", "Receive Message" -> p5, p5 -> "Send Acknowledgement", "Send Acknowledgement" -> p6, "Send Acknowledgement" -> p8, p8 -> "Person 2", "Person 2" -> p2, p2 -> "Receive Message", p6 -> "Receive Acknowledgement"}, {0, 2, 0,
6, 1, 1, 2, 1}, 2, "TokenFirings"]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/4923a78980f04553.png)

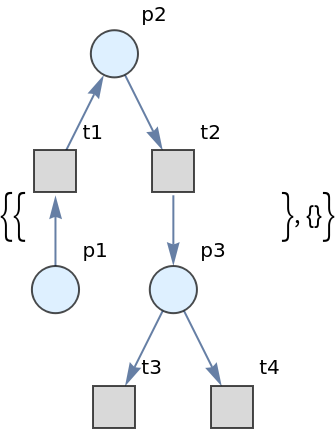
![petriNet = ResourceFunction["MakePetriNet"][{p1, p2, p3, "Buffer", p4}, {"Produce", t1, t2, "Consume"}, {p1 -> "Produce", "Produce" -> p3, p3 -> t2, t2 -> p1, t2 -> "Buffer", "Buffer" -> t1, t1 -> p4, p4 -> "Consume", "Consume" -> p2, p2 -> t1}, {1, 3, 0, 6, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/7b6d181c1dab2b3d.png)

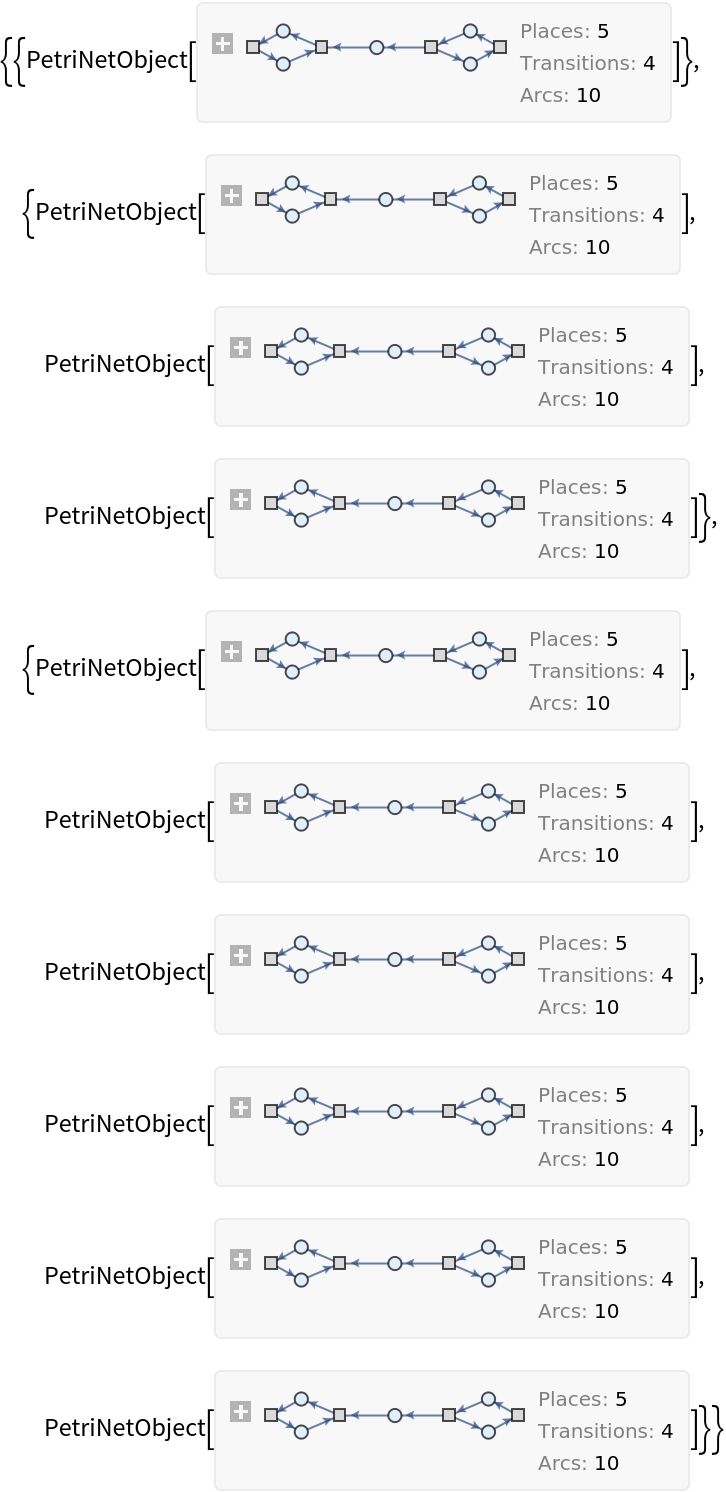


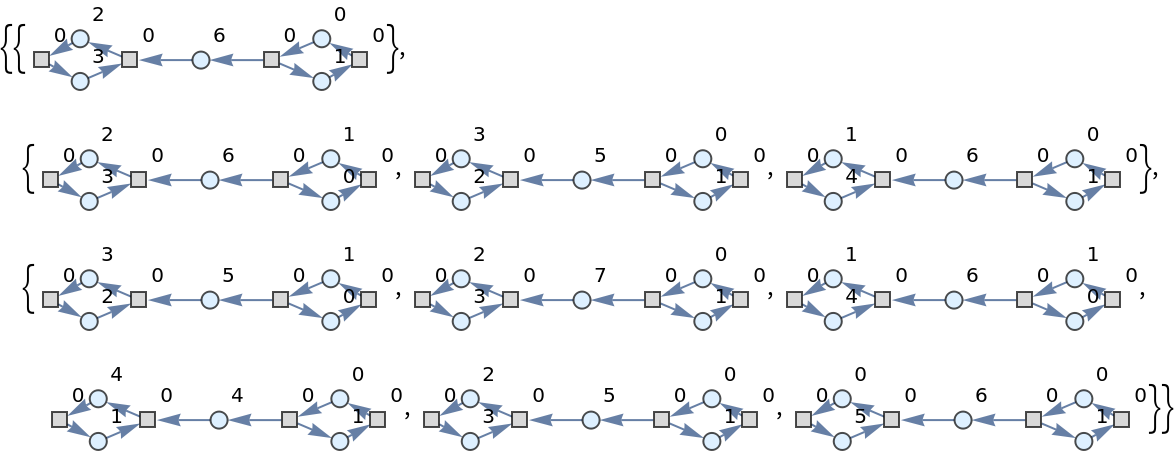

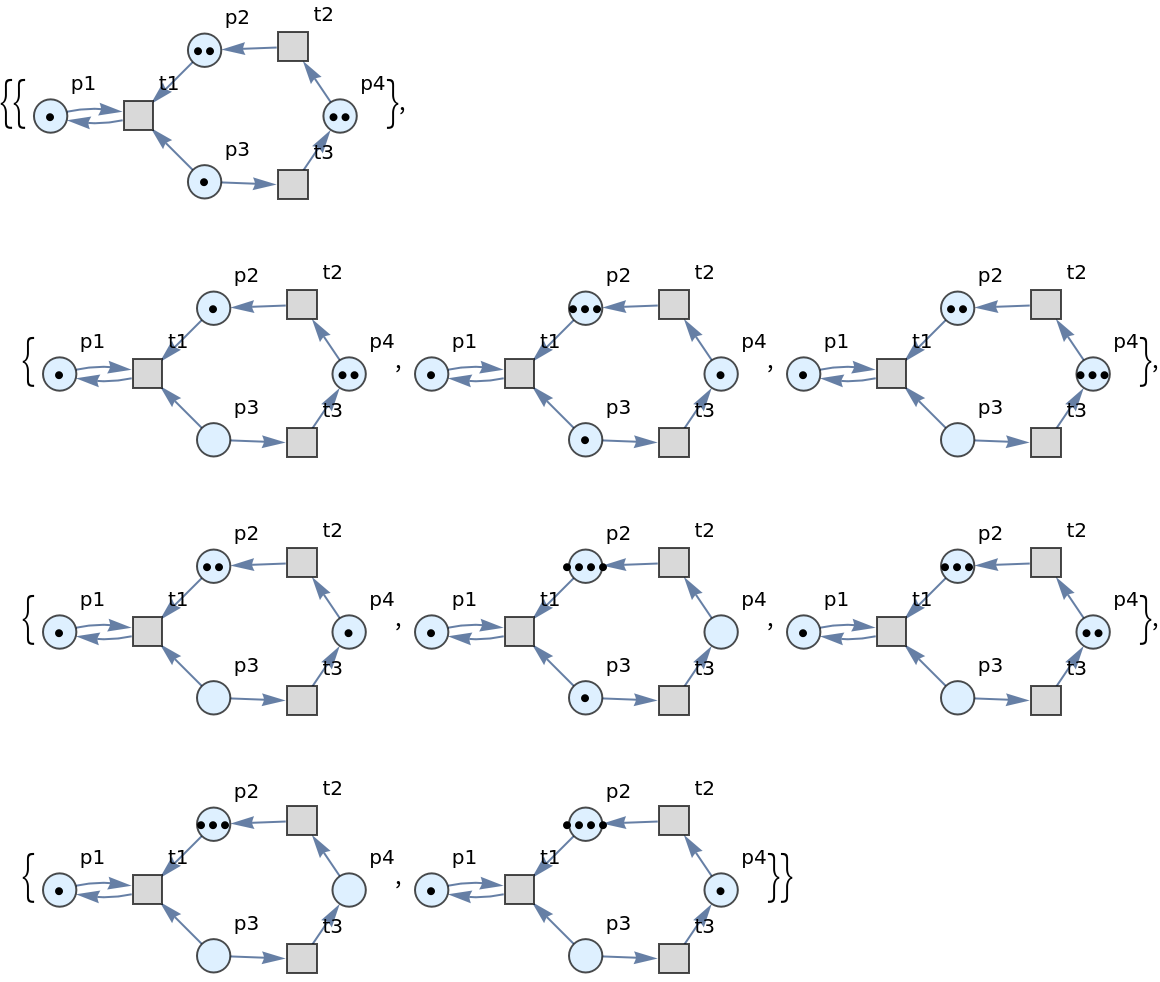
![ResourceFunction[
"PetriNetMultiwayEvolution"][{p1, p2, p3, p4}, {t1, t2, t3}, {p1 -> t1, t1 -> p1, p2 -> t1, p3 -> t1, t2 -> p2, p3 -> t3, t3 -> p4, p4 -> t2}, {1, 2, 1, 2}, "LabeledGraphs"]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/4be8ca5022fd10ba.png)

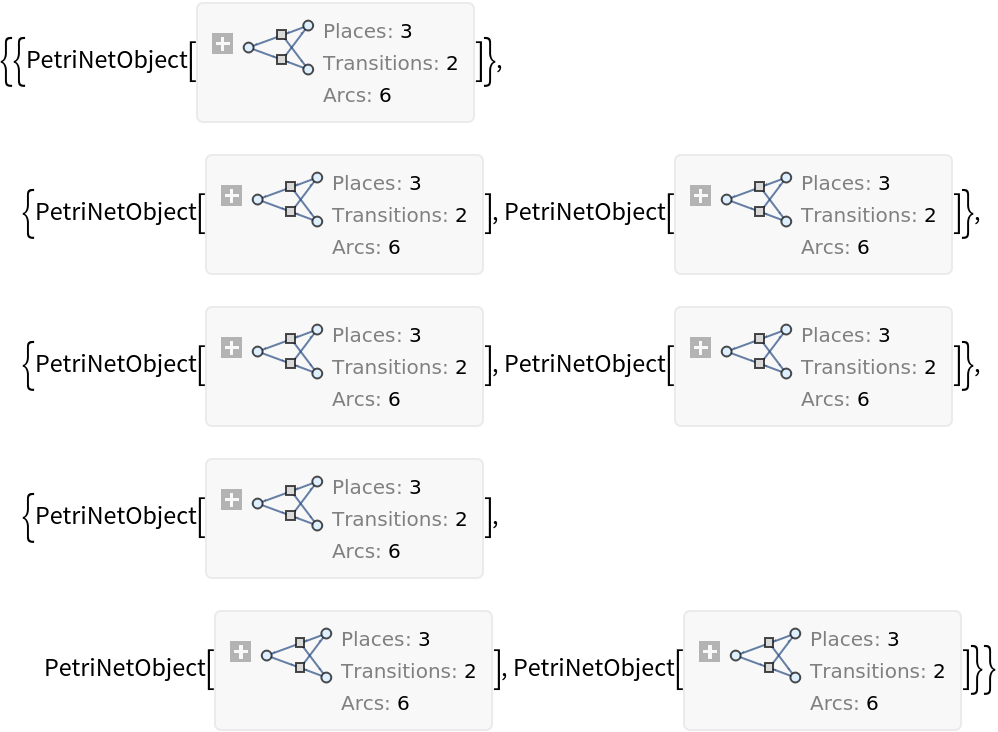
![ResourceFunction[
"PetriNetMultiwayEvolution"][{p1, p2, p3, p4}, {t1, t2, t3}, {p1 -> t1, t1 -> p1, p2 -> t1, p3 -> t1, t2 -> p2, p3 -> t3, t3 -> p4, p4 -> t2}, {1, 2, 1, 2}, "LabeledGraphs", VertexSize -> 0.1]](https://www.wolframcloud.com/obj/resourcesystem/images/9ee/9ee39ff2-4589-4094-917e-23d3a5694f2a/5e160e75815e7a60.png)
