Function Repository Resource:

PersianImmortals

Source Notebook

Simulate the self-organizing system of the Persian Immortals as described by Herodotus

Contributed by: Sander Huisman

ResourceFunction["PersianImmortals"][]

simulates 10⁴ agents where the weakest agent is removed at every step and replaced by a new agent.

ResourceFunction["PersianImmortals"][n]

simulates 10⁴ agents where n of the weakest agents are removed and replaced by new agents.

ResourceFunction["PersianImmortals"][{n,m}]

simulates 10⁴ agents where n of the weakest agents and m random agents are removed.

ResourceFunction["PersianImmortals"][…,pop]

starts with an agent population pop.

ResourceFunction["PersianImmortals"][…,pop,tspec]

runs the simulation according to the time specification tspec.

ResourceFunction["PersianImmortals"][…,pop,tspec,bins]

uses the binning specification bins.

Details and Options

The Persian Immortals were an elite army described by the Greek historian and geographer Herodotus while attacking Greece in 480-479 BCE under Xerxes's command. Their name refers to the fact that the size of the army was always kept constant at 10000 by immediately replacing every fallen warrior with a warrior from reserve troops. Because of this tactic, morale was kept high, and the army was actually getting stronger over time.

n determines how many of the weakest agents are removed:

Integer, remove the n weakest agents.

dist

Use the distribution dist to determine how many of the weakest agents are removed.

m determines how random agents are removed:

Integer, remove m agents randomly

dist

Use the distribution dist to determine how many random agents are removed

{dist}

Each agent gets a random threshold between 0 and its fitness. This threshold is then compared to a random attack given by dist. Fitter agents have a higher chance of survival.

pop describes the initial population:

Integer, n agents of fitnesses linearly chosen between 0 and 1.

Automatic

Use 10⁴ agents of fitnesses linearly chosen between 0 and 1.

{f₁, f₂,…}

Use agents with fitness f_i (should be between 0 and 1).

tspec describes the time for storing the output:

Integer, simulate n steps and save data from all timesteps.

{t_min,t_max,Δt}

Simulates for t_max steps but saves every Δt steps, starting from t_min.

Simulates until Max[t_i] and saves each t_i.

bins should be an integer that describes in how much bins the data should be binned. Fitnesses are assumed to be between 0 and 1.

PersianImmortals takes the following options:

"Repetitions"

Automatic

number of times to simulate

"NewFitness"

Automatic

fitness for new agents

"Strengthening"

Automatic

specifies how the surviving agents strengthen over time

Possible settings for the option "Repetitions" include:

Automatic

perform a single simulation

perform n simulations and average the results

Possible settings for the option "NewFitness" include:

Automatic

generate agents with random fitnesses uniformly taken between 0 and 1 (UniformDistribution[0,1])

dist

generate agents with random fitnesses taken from the distribution dist

Possible settings for the option "Strengthening" include:

Automatic

agents do not become stronger (equivalent to 0)

val≤1

after each time step val is added to the fitness and clipped to[0,1]

val>1

after each time step the fitness is multiplied by val and clipped to[0,1]

Scaled[val]

after each time step the fitness gets a fraction val closer to 1

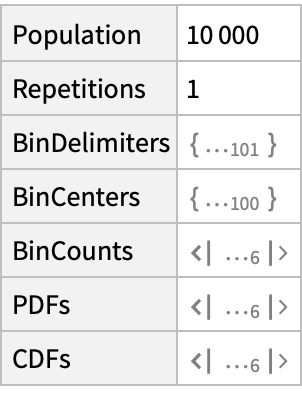
ResourceFunction["PersianImmortals"] returns an Association with the following keys: "Population", "Repetitions", "BinDelimiters", "BinCenters", "BinCounts", "PDFs" and "CDFs".

Examples

Basic Examples (4)

Perform a simulation where, in each time-step, the weakest agent is replaced by a new random agent:

In[1]:=

Out[2]=

Visualize the probability density function (PDF) for the fitness of the agents at various times:

In[3]:=

Out[3]=

At each step remove a random number between 1 and 10 of the weakest agents:

In[4]:=

Out[5]=

At each step remove between 1 and 5 of the weakest agents and between 1 and 3 random agents:

In[6]:=

i = ResourceFunction[
"PersianImmortals"][{DiscreteUniformDistribution[{1, 5}], DiscreteUniformDistribution[{1, 3}]}];
ListLinePlot[Values[i["PDFs"]], PlotLegends -> Keys[i["PDFs"]], PlotRange -> {0, All}]

Out[7]=

Do not remove the weakest agents, but rather randomly remove agents based on a probabilistic distribution. Each agents creates a random threshold in the Range[0,fitness] and this is compared against a random number given by a distribution:

In[8]:=

Out[9]=

Scope (2)

Use an army of 100 agents:

In[10]:=

$i = ResourceFunction["PersianImmortals"][{1, 1}, 10^2, Sequence[{0, 400, 40}, "Repetitions" -> 250]]; ListLinePlot[Values[i["PDFs"]], PlotLegends -> Keys[i["PDFs"]], PlotRange -> {0, All}]$

Out[11]=

Use more bins to get more detailed probability density functions:

In[12]:=

$i = ResourceFunction["PersianImmortals"][{1, 1}, 10^4, {0, 15000, 1000}, 250]; ListLinePlot[Values[i["PDFs"]], PlotLegends -> Keys[i["PDFs"]], PlotRange -> {0, All}]$

Out[13]=

Options (7)

NewFitness (2)

Use a different fitness distribution for new agents:

In[14]:=

Out[15]=

Use this distribution:

In[16]:=

$i = ResourceFunction["PersianImmortals"][{1, 1}, 10^4, {0, 15000, 1000}, "NewFitness" -> dist]; ListLinePlot[Values[i["CDFs"]], PlotLegends -> Keys[i["CDFs"]], PlotRange -> {0, All}]$

Out[17]=

Create agents with a normal distribution that is truncated such that the fitness is always between 0 and 1:

In[18]:=

Out[19]=

Simulate with this fitness distribution for new agents:

In[20]:=

$i = ResourceFunction["PersianImmortals"][{1, 0}, 10^4, {0, 15000, 1000}, "NewFitness" -> dist]; ListLinePlot[Values[i["CDFs"]], PlotLegends -> Keys[i["CDFs"]], PlotRange -> {0, All}]$

Out[21]=

Repetitions (2)

A single run of the simulation gives jagged results for the probability density function:

In[22]:=

$i = ResourceFunction["PersianImmortals"][{1, 2}, 10^4, {0, 5000, 1000}]; ListLinePlot[Values[i["PDFs"]], PlotLegends -> Keys[i["PDFs"]], PlotRange -> {0, All}]$

Out[23]=

Repeat the simulation and average:

In[24]:=

$i = ResourceFunction["PersianImmortals"][{1, 2}, 10^4, {0, 5000, 1000}, "Repetitions" -> 25]; ListLinePlot[Values[i["PDFs"]], PlotLegends -> Keys[i["PDFs"]], PlotRange -> {0, All}]$

Out[25]=

Strengthening (3)

In case of survival of an agent, add 0.0001 to their fitness:

In[26]:=

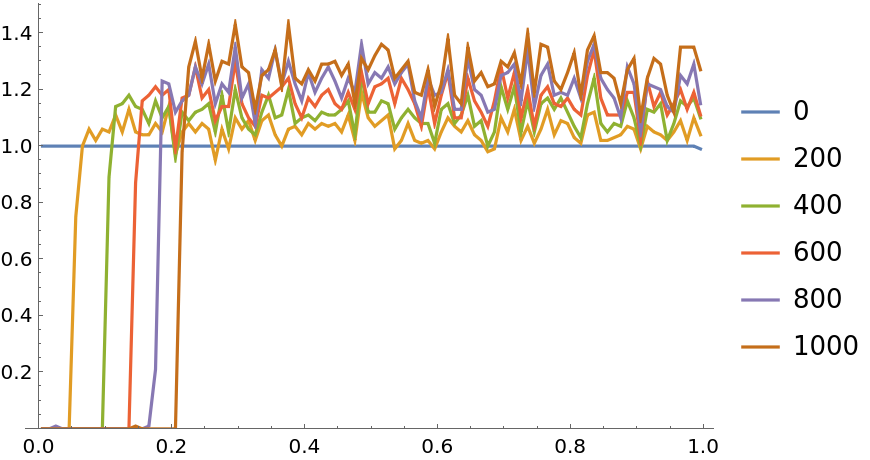
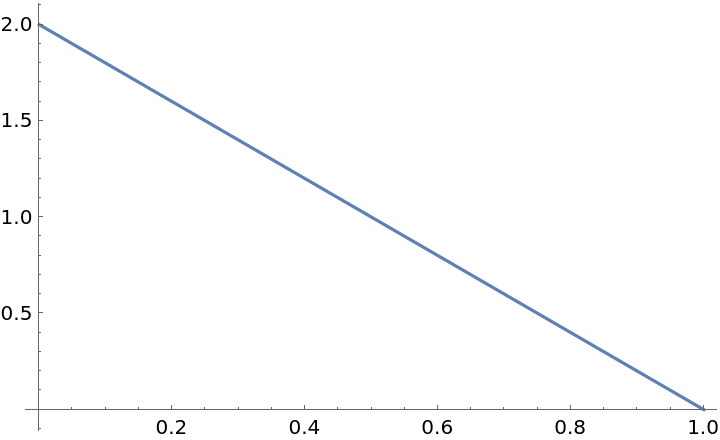
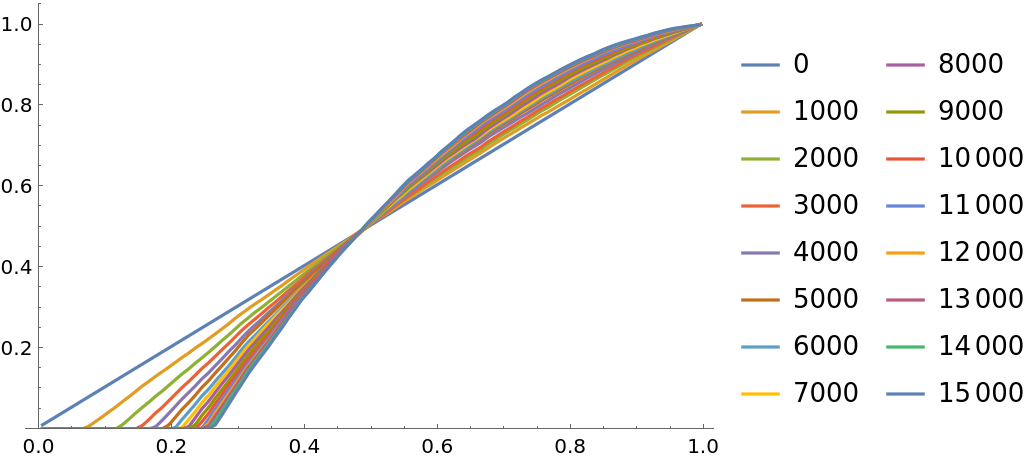
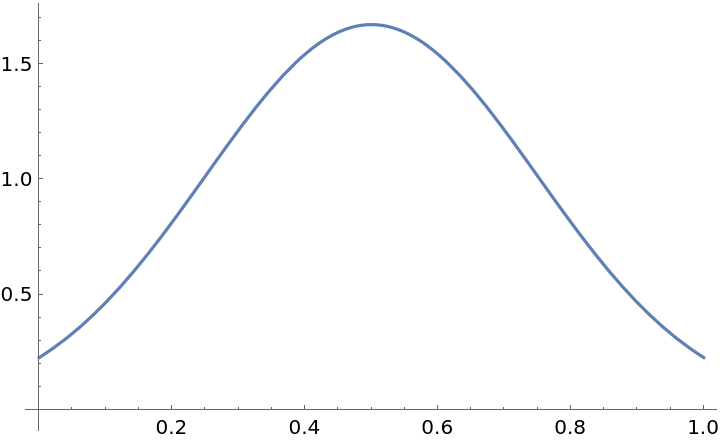
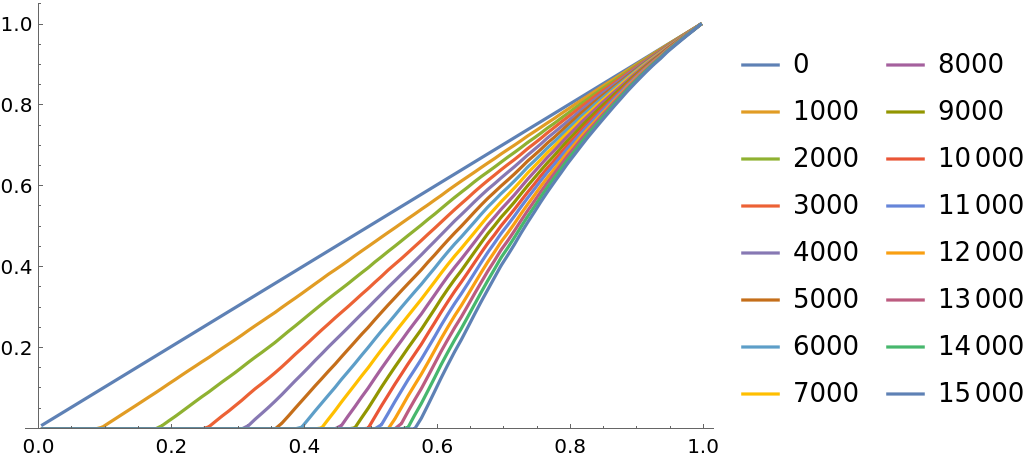
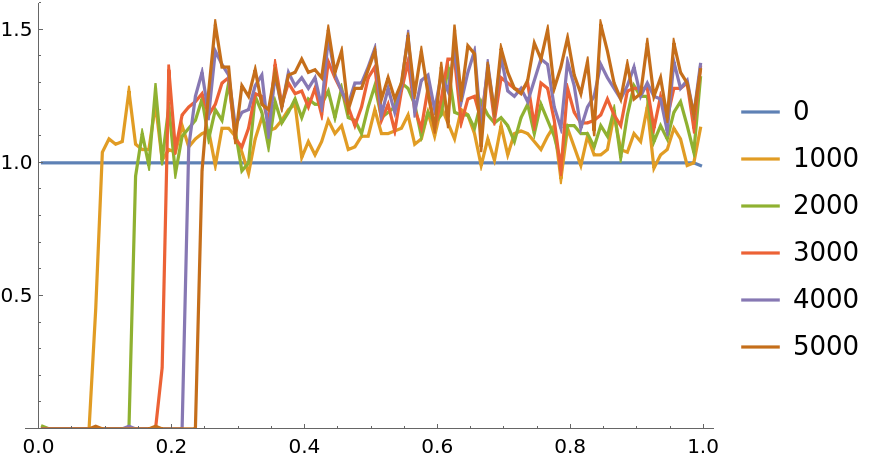
$i = ResourceFunction["PersianImmortals"][{1, 3}, 10^4, {0, 10^4, 1000}, "Strengthening" -> 0.0001, "Repetitions" -> 10]; ListLinePlot[Values[i["CDFs"]], PlotLegends -> Keys[i["CDFs"]], PlotRange -> {0, All}]$

Out[27]=

In case of survival of an agent, multiply their fitness by 1.0003:

In[28]:=

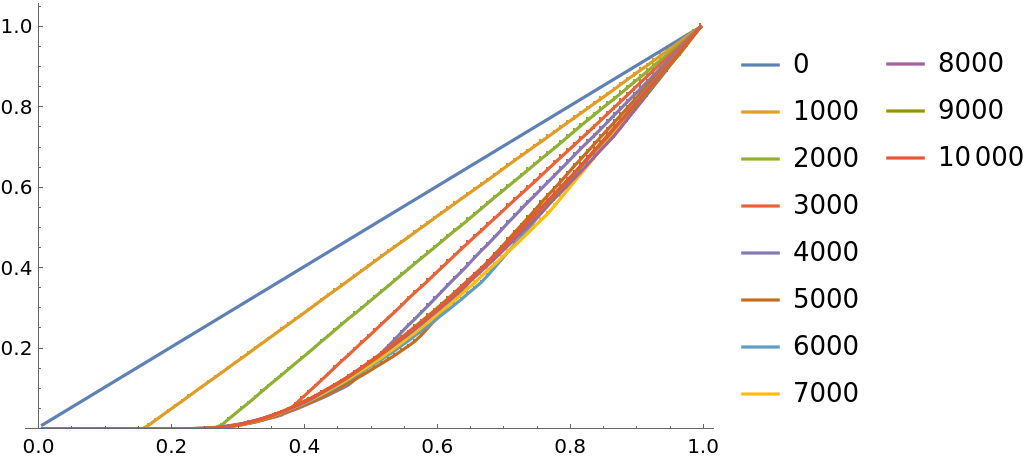
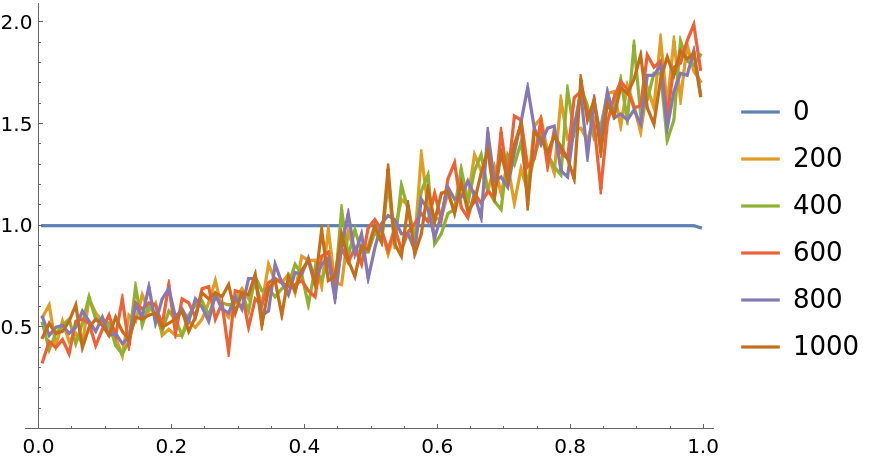
$i = ResourceFunction["PersianImmortals"][{1, 3}, 10^4, {0, 10^4, 1000}, "Strengthening" -> 1.0003, "Repetitions" -> 10]; ListLinePlot[Values[i["CDFs"]], PlotLegends -> Keys[i["CDFs"]], PlotRange -> {0, All}]$

Out[29]=

In case of survival of an agent, improve their fitness by bring it 0.05% closer to 1:

In[30]:=

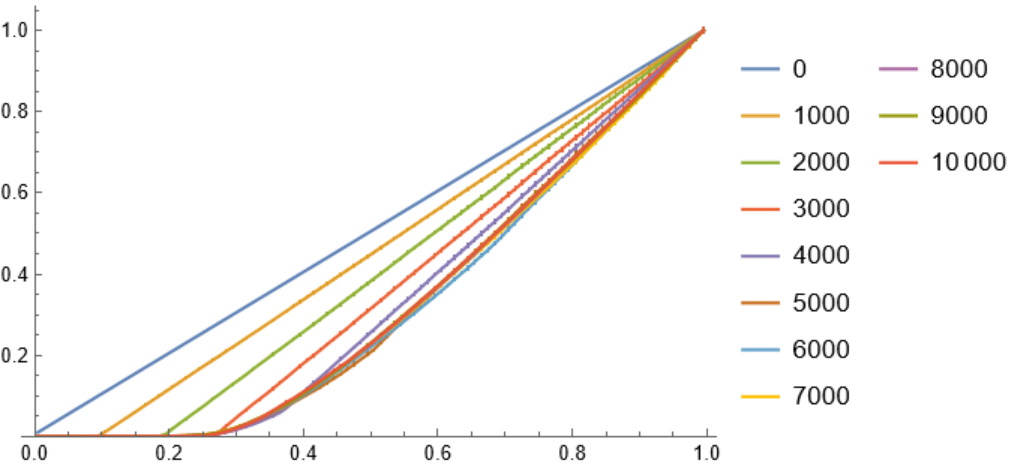
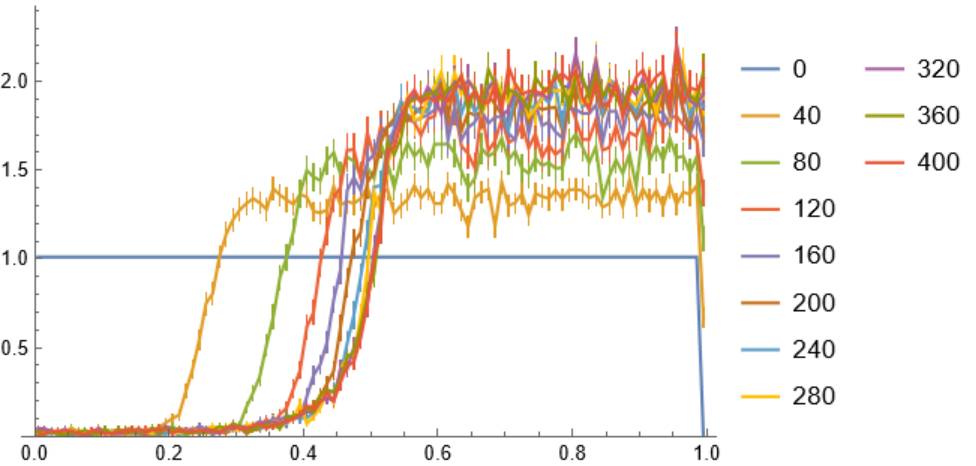
$i = ResourceFunction["PersianImmortals"][{1, 3}, 10^4, {0, 15000, 500}, "Strengthening" -> Scaled[0.0005], "Repetitions" -> 1]; ListLinePlot[Values[i["CDFs"]], PlotLegends -> Keys[i["CDFs"]], PlotRange -> {0, All}]$

Out[31]=

Neat Examples (3)

Find the mean strength of the agents:

In[32]:=

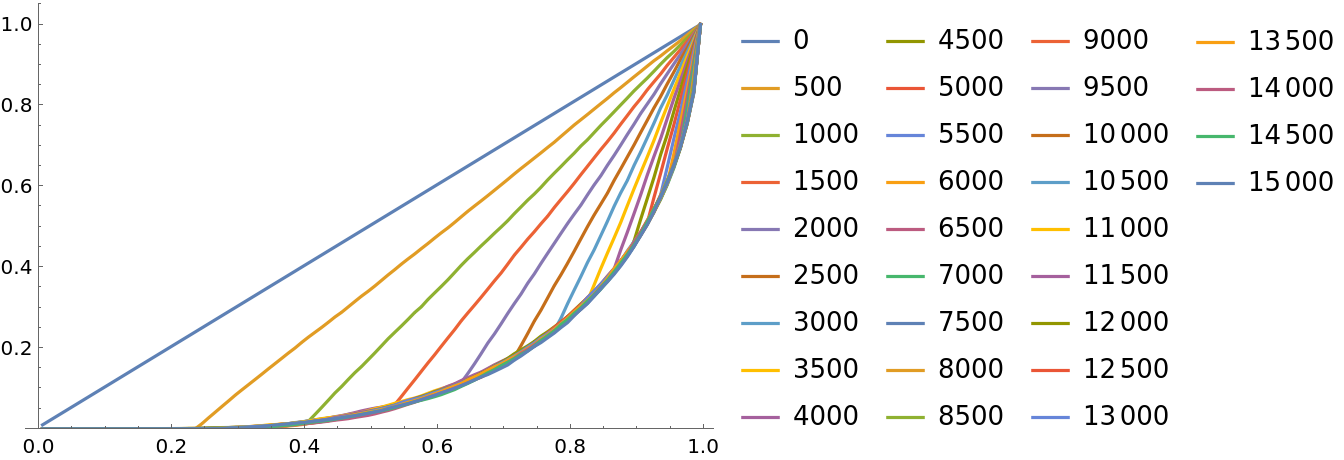
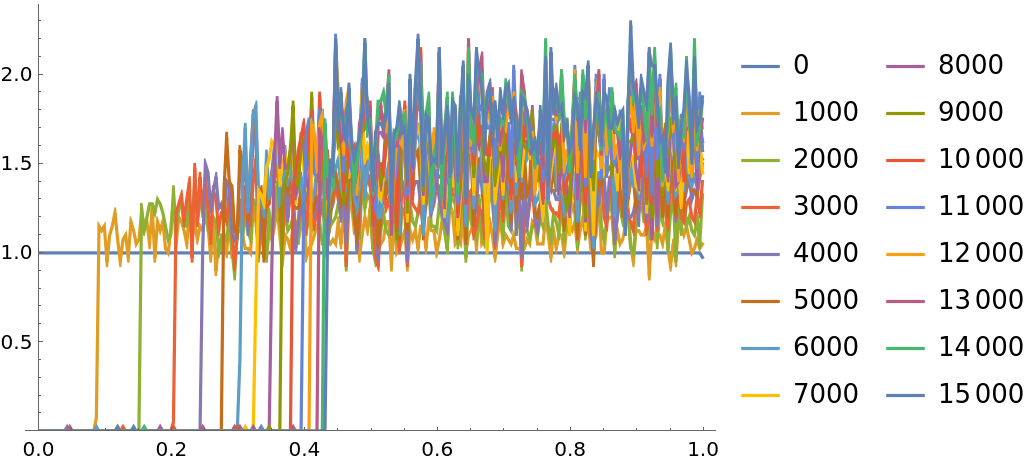
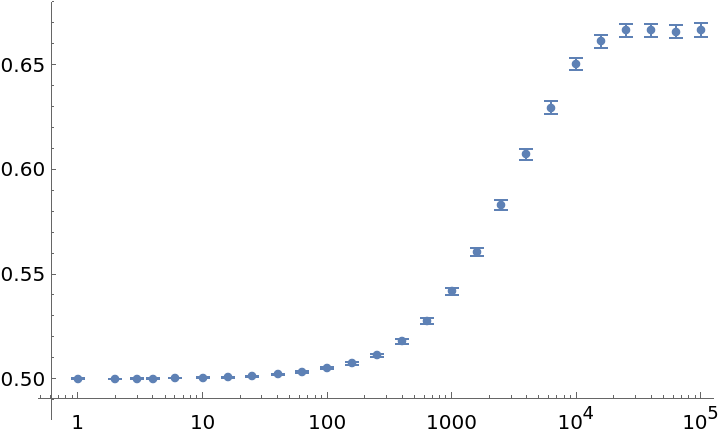
$ts = Round[10^Range[0, 5, 1/5]]; i = ResourceFunction["PersianImmortals"][{1, 2}, 10^4, {ts}, "Repetitions" -> 5]; widths = Differences[i["BinDelimiters"]]; meanstrengths = MapApply[Times]/*(# . widths &) /@ Values[i["PDFs"]]; ListLogLinearPlot[{Keys[i["PDFs"]], meanstrengths} // Transpose]$

Out[36]=

Randomly remove agents based on a small chance:

In[37]:=

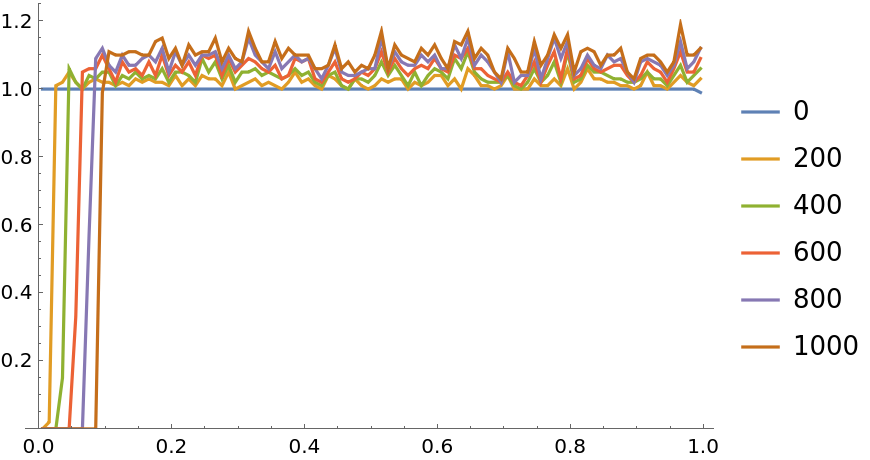
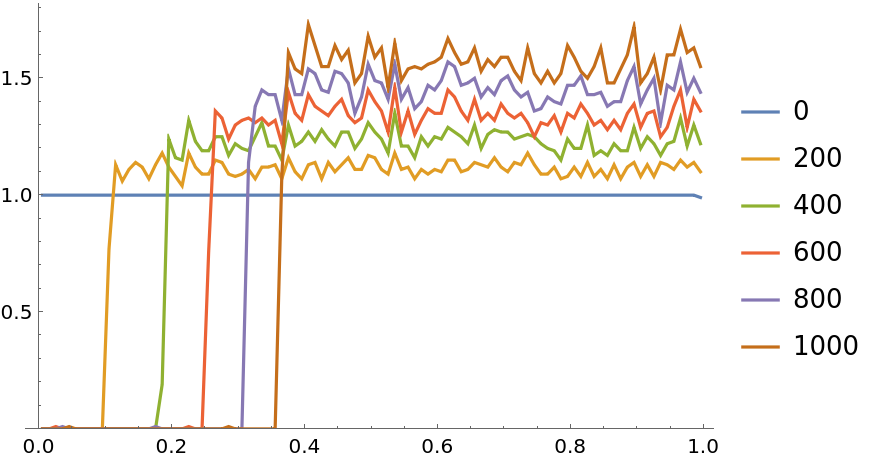
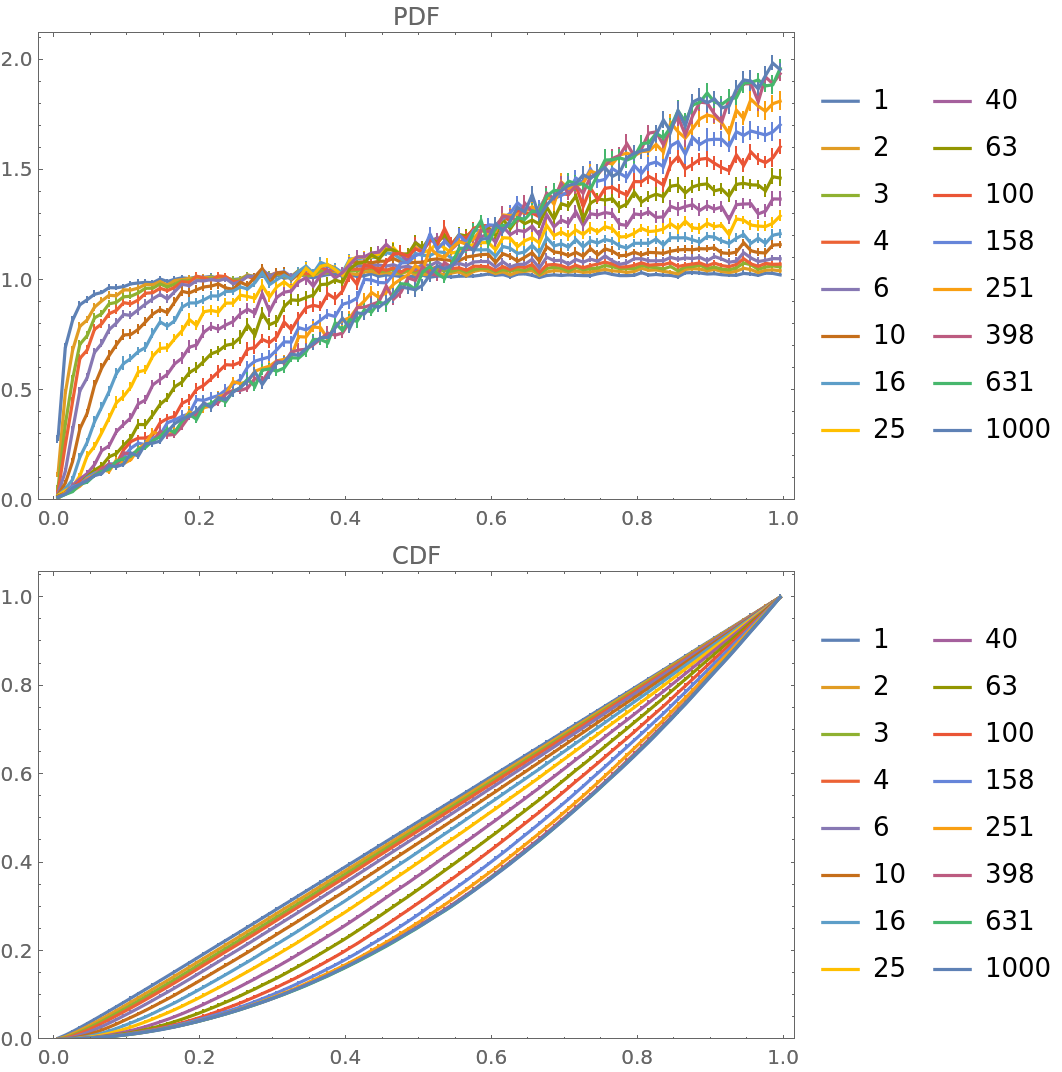
$ts = Round[10^Range[0, 3, 1/5]]; i = ResourceFunction[ "PersianImmortals"][{0, {UniformDistribution[{0, 0.01}]}}, 10^4, {ts}, "Repetitions" -> 15]; { ListLinePlot[Values[i["PDFs"]], PlotLegends -> Keys[i["PDFs"]], PlotRange -> {0, All}, ImageSize -> 400, PlotLabel -> "PDF", Frame -> True], ListLinePlot[Values[i["CDFs"]], PlotLegends -> Keys[i["CDFs"]], PlotRange -> {0, All}, ImageSize -> 400, PlotLabel -> "CDF", Frame -> True] } // Column$

Out[39]=

Use a different fitness distribution for new agents:

In[40]:=

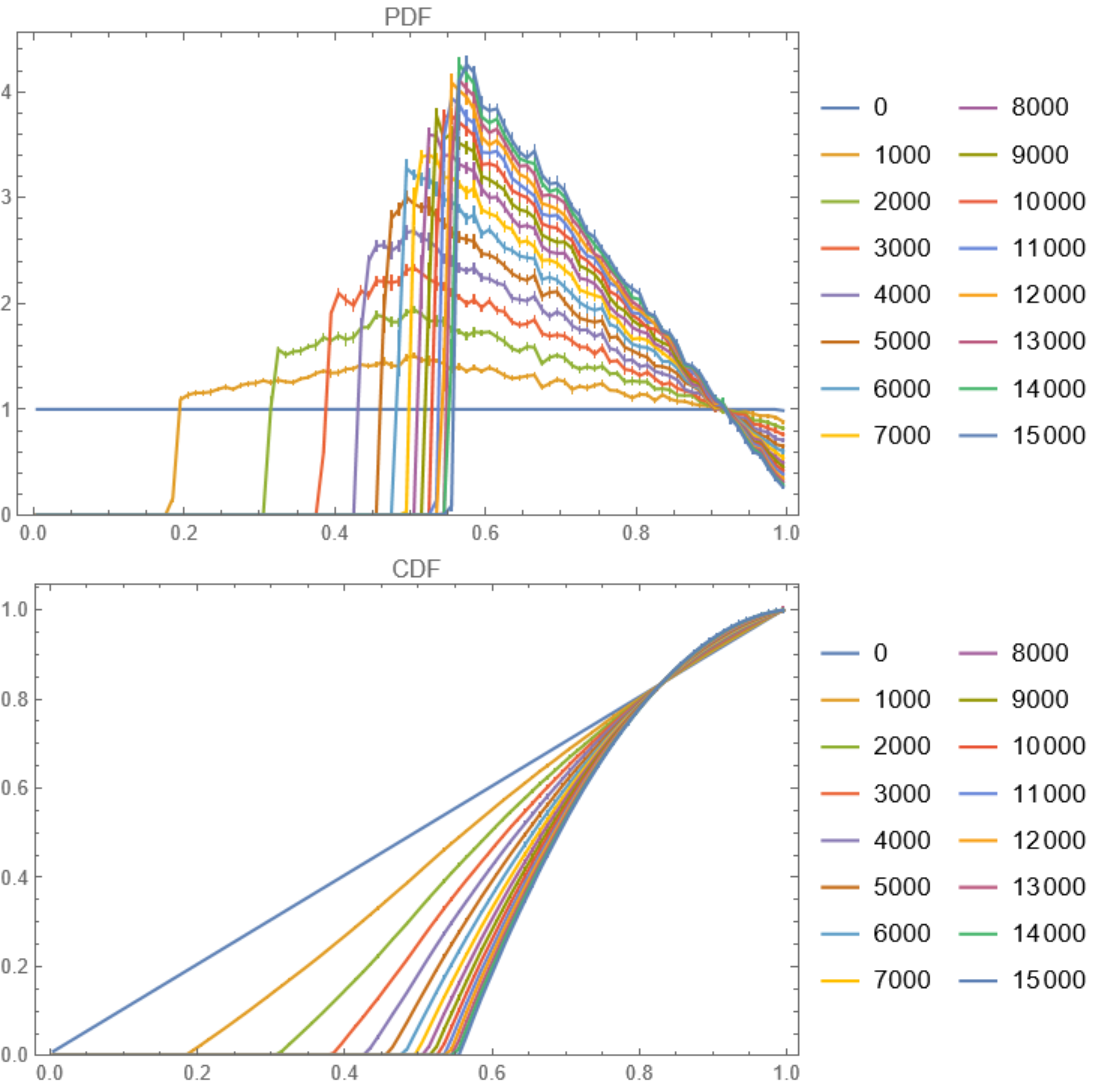
$dist = TriangularDistribution[{0, 1}]; i = ResourceFunction["PersianImmortals"][{2, 1}, 10^4, {0, 15000, 1000}, "Repetitions" -> 10, "NewFitness" -> dist]; { ListLinePlot[Values[i["PDFs"]], PlotLegends -> Keys[i["PDFs"]], PlotRange -> {0, All}, ImageSize -> 400, PlotLabel -> "PDF", Frame -> True], ListLinePlot[Values[i["CDFs"]], PlotLegends -> Keys[i["CDFs"]], PlotRange -> {0, All}, ImageSize -> 400, PlotLabel -> "CDF", Frame -> True] } // Column$

Out[42]=

Publisher

SHuisman

Version History

1.1.0 – 22 February 2023
1.0.0 – 13 February 2023

Source Metadata

Citation:
- Kanellopoulos, Giorgos, Dimitrios Razis, and Ko van der Weele. "The Persian Immortals: A classical case of self-organization." American Journal of Physics 88, no. 4, 263-268 (2020).
  DOI: 10.1119/10.0000834

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

PersianImmortals

Details and Options