Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PerpendicularSurface

Source Notebook

Compute the perpendicular surface of a curve

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["PerpendicularSurface"][c,t,{u,v},φ]

computes the perpendicular surface with respect to variables u and v, making an angle ϕ with the normal surface of the curve parameterized by t.

Details and Options

For any space curve α, there are other surfaces which lie between the normal surface and the binormal surface of the form , where , are the normal and binormal vector fields to α and sp[0,α] the normal surface of α and sp[π,α] the binormal surface.
The perpendicular surface is effectively a ruled surface.

Examples

Basic Examples (2) 

Viviani's curve:

In[1]:=
viviani = Entity["SpaceCurve", "VivianiCurve"]["ParametricEquations"][1][t]
Out[1]=

Plot it:

In[2]:=
vp = ParametricPlot3D[Evaluate[viviani], {t, -2 \[Pi], 2 \[Pi]}, PlotStyle -> Thickness[.02]]
Out[2]=

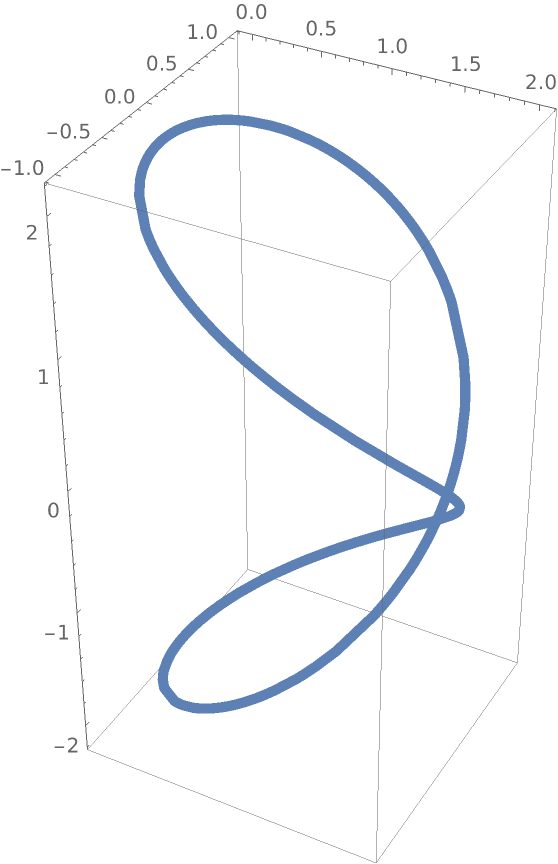
Compute the perpendicular surface for Viviani's curve:

In[3]:=
ResourceFunction[ "PerpendicularSurface"][{1 + Cos[t], Sin[t], 2 Sin[t/2]}, t, {u, v}, \[Phi]] // Simplify
Out[3]=

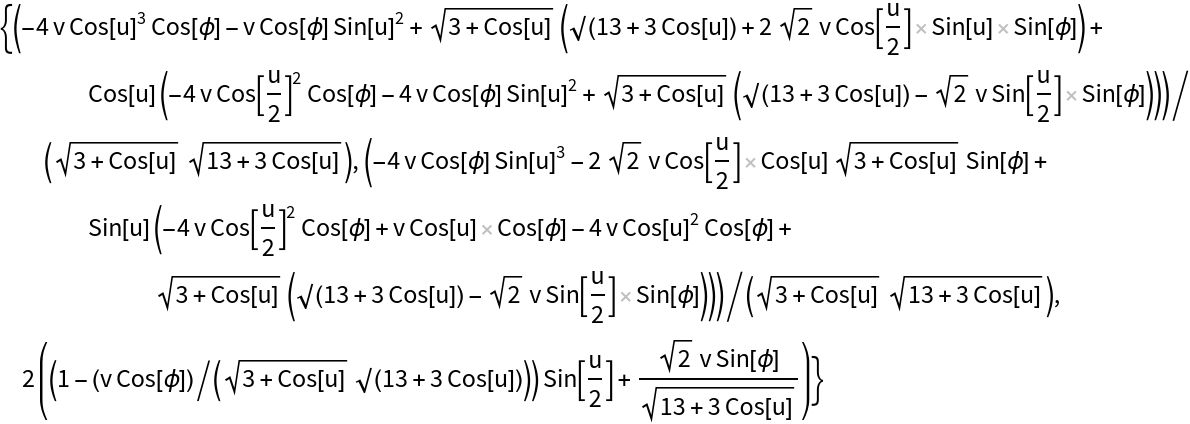
Plot both, varying the angle φ:

In[4]:=
Manipulate[ Show[vp, ParametricPlot3D[ Evaluate[ ResourceFunction[ "PerpendicularSurface"][{1 + Cos[t], Sin[t], 2 Sin[t/2]}, t, {u, v}, \[Phi]]], {u, -2 \[Pi], 2 \[Pi]}, {v, -.5, .5}, PlotPoints -> {80, 10}, PlotStyle -> Yellow], PlotRange -> {{-0.5, 2.5}, {-1.4, 1.4}, {-2.7, 2.7}}], {\[Phi], 0, 2 \[Pi]}]
Out[4]=

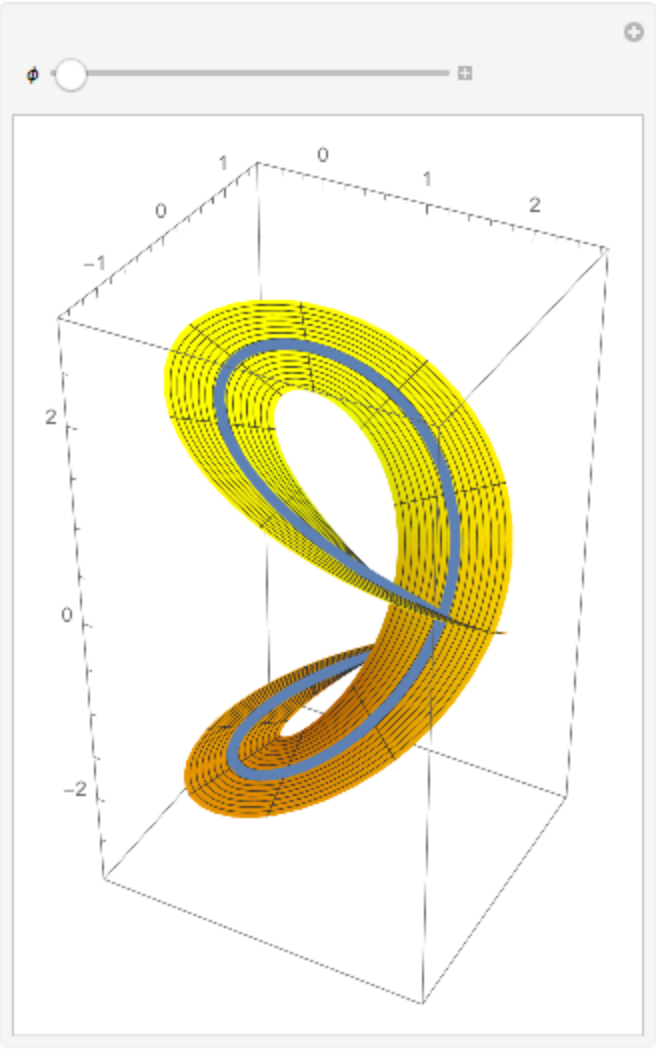
The normal and binormal surfaces are special cases. Define Viviani's curve and compute its perpendicular surface:

In[5]:=
viviani = Entity["SpaceCurve", "VivianiCurve"]["ParametricEquations"][1][t] ResourceFunction[ "PerpendicularSurface"][{1 + Cos[t], Sin[t], 2 Sin[t/2]}, t, {u, v}, \[Phi]] - ResourceFunction["NormalSurface"][viviani, t, {u, v}] // Simplify
Out[5]=

Compute the normal surface:

In[6]:=
ns = ResourceFunction["NormalSurface"][viviani, t, {u, v}] // Simplify
Out[6]=

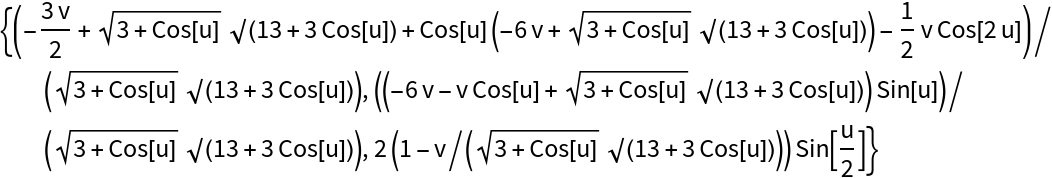
Compute the binormal surface:

In[7]:=
bs = ResourceFunction["BinormalSurface"][viviani, t, {u, v}] // Simplify
Out[7]=

Plots of normal and binormal surfaces:

In[8]:=
nsp = ParametricPlot3D[ Evaluate[ns], {u, -2 \[Pi], 2 \[Pi]}, {v, -1, -.05}, PlotPoints -> {80, 10}, PlotStyle -> Green];
In[9]:=
bsp = ParametricPlot3D[ Evaluate[bs], {u, -2 \[Pi], 2 \[Pi]}, {v, .05, 1}, PlotPoints -> {80, 10}, PlotStyle -> Red];

Combining the previous surfaces and Viviani's curve with an intermediate surface:

In[10]:=
Show[vp, nsp, bsp, ParametricPlot3D[ Evaluate[ResourceFunction[ "PerpendicularSurface"][{1 + Cos[t], Sin[t], 2 Sin[t/2]}, t, {u, v}, 3 \[Pi]/4]], {u, -2 \[Pi], 2 \[Pi]}, {v, .05, 1}, PlotPoints -> {80, 10}, PlotStyle -> Yellow]]
Out[10]=

Neat Examples (1) 

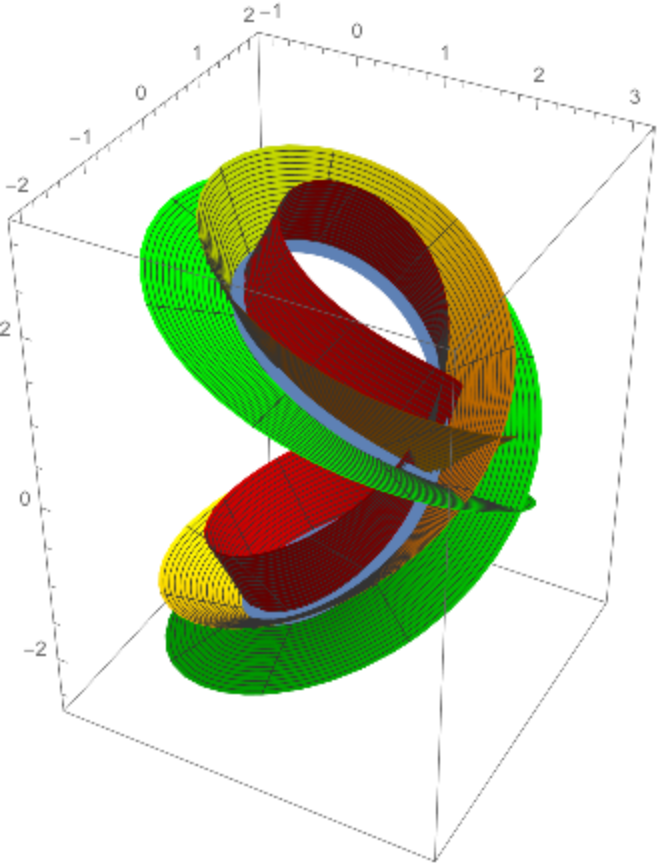
Perpendicular surface for the spherical spiral:

In[11]:=
With[{a = 1, m = 3, n = 5}, ParametricPlot3D[ Evaluate[ResourceFunction[ "PerpendicularSurface"][{a Cos[m t] Cos[n t], a Sin[m t] Cos[n t], a Sin[n t]}, t, {u, v}, 1]], {u, -2 \[Pi], 2 \[Pi]}, {v, -.25, .25}, PlotPoints -> {80, 10}, PlotStyle -> Yellow, Axes -> False, Boxed -> False, Mesh -> None]]
Out[11]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 17 September 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information