Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the permutation graph of a permutation
ResourceFunction["PermutationGraph"][p] gives the permutation graph for the permutation p. |
GraphComplement gives the permutation graph of the reverse permutation p:
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= | 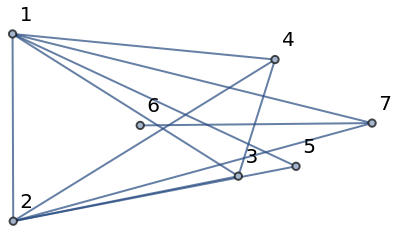 |
| In[4]:= |
| Out[4]= | 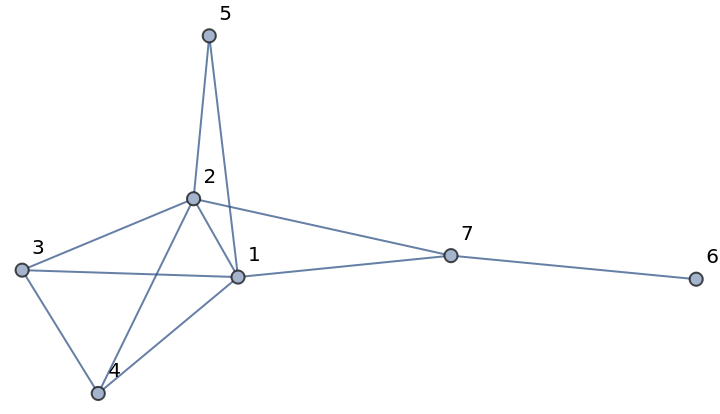 |
| In[5]:= |
| Out[5]= |
The number of inversions in a permutation can be computed by the resource function InvesionCount and is equal to the number of edges in its permutation graph:
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= |
Every clique in a permutation graph corresponds to a decreasing sequence in the corresponding permutation:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| In[10]:= |
| Out[10]= |
A maximum-size clique corresponds to one of the longest decreasing sequences:
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= | 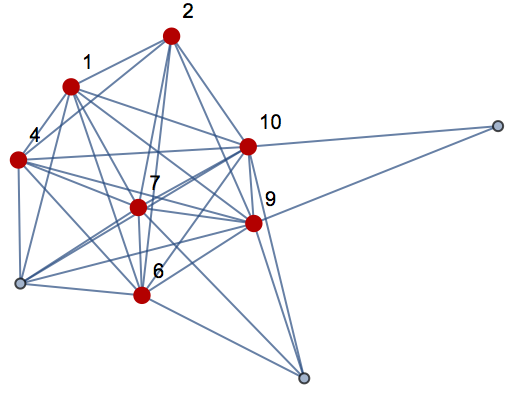 |
This work is licensed under a Creative Commons Attribution 4.0 International License