Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Give the permutation corresponding to a given length and lexicographic index
ResourceFunction["PermutationFromIndex"][index,length] gives the permutation with a given lexicographic index and length. |
Give the first permutation of length 4:
| In[1]:= |
| Out[1]= |
Give the last permutation of length 4:
| In[2]:= |
| Out[2]= |
Give the 777th permutation of length 7:
| In[3]:= |
| Out[3]= |
Permutations with an arbitrarily large lexicographic index can returned:
| In[4]:= |
| Out[4]= | 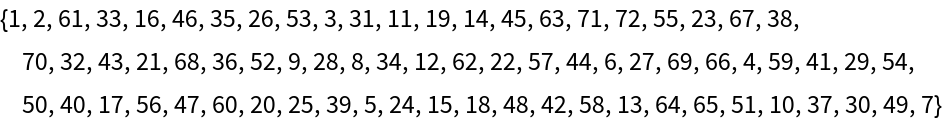 |
When an index for length n exceeds n!, the index is considered mod n!:
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
Permutations halfway through the index:
| In[7]:= |
| Out[7]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License