Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
A graph representing cycles and fixed points of a permutation
ResourceFunction["PermutationCyclesGraph"][perm] constructs a graph of disjoint cycles representing the permutation perm. |
Permutation cycles represented as a graph:
| In[1]:= |
|
| In[2]:= |
|
| Out[2]= |
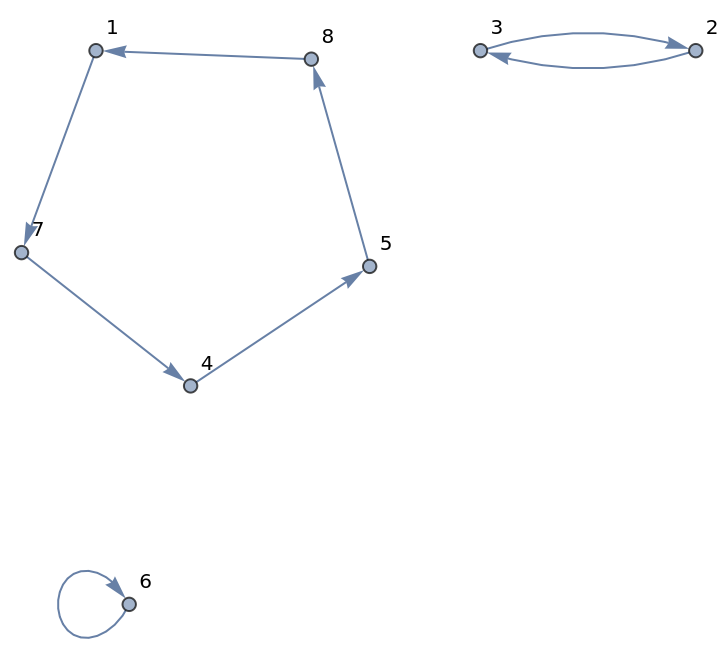
|
Or as a list:
| In[3]:= |
|
| Out[3]= |
|
Cycles graph of a permutation list:
| In[4]:= |
|
| Out[4]= |
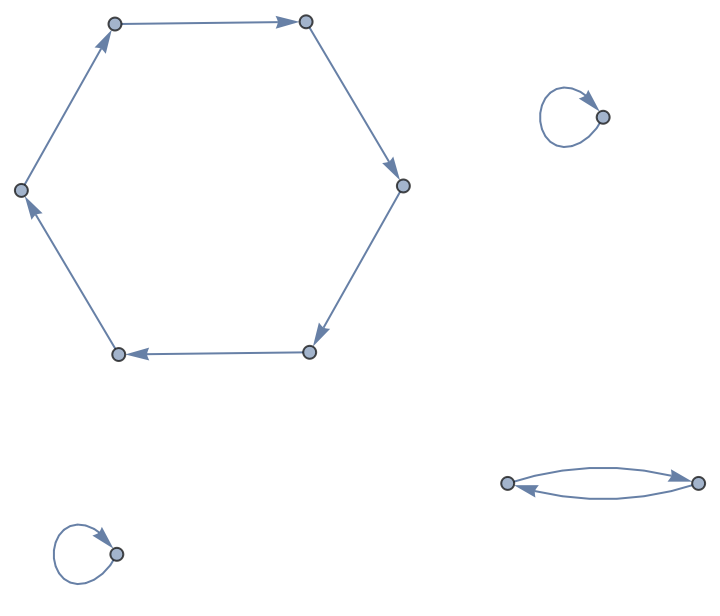
|
Permutation represented as Cycles:
| In[5]:= |
|
| Out[5]= |
|
| In[6]:= |
|
| Out[6]= |
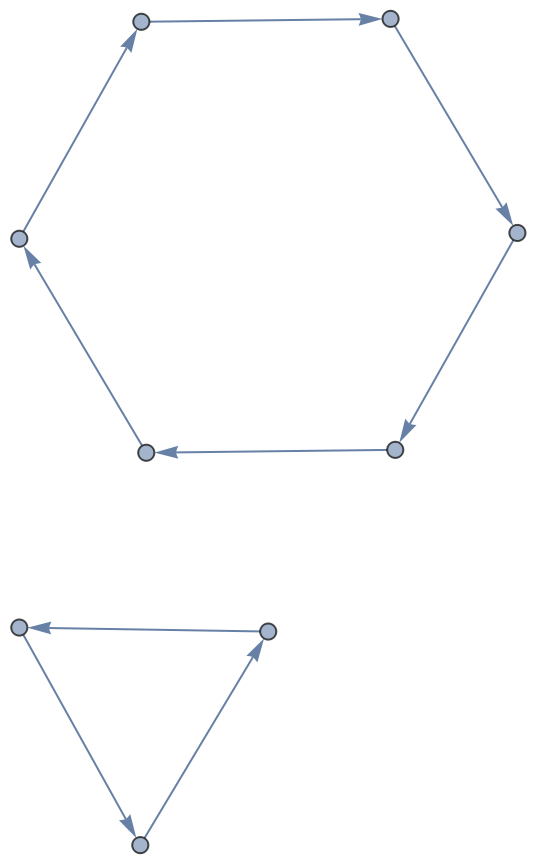
|
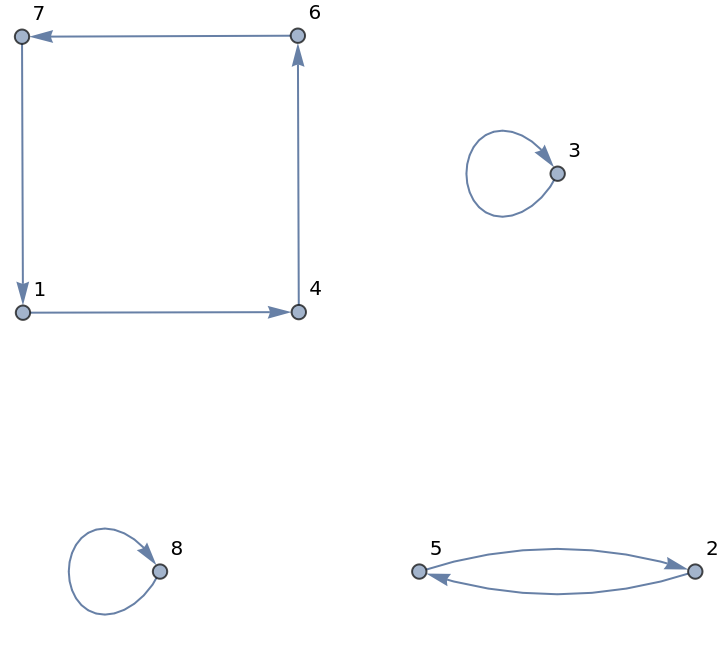
Permutation cycles graph can also be constructed, possibly less efficiently, by finding the ordering of a permutation:
| In[7]:= |
|
| In[8]:= |
|
| Out[8]= |
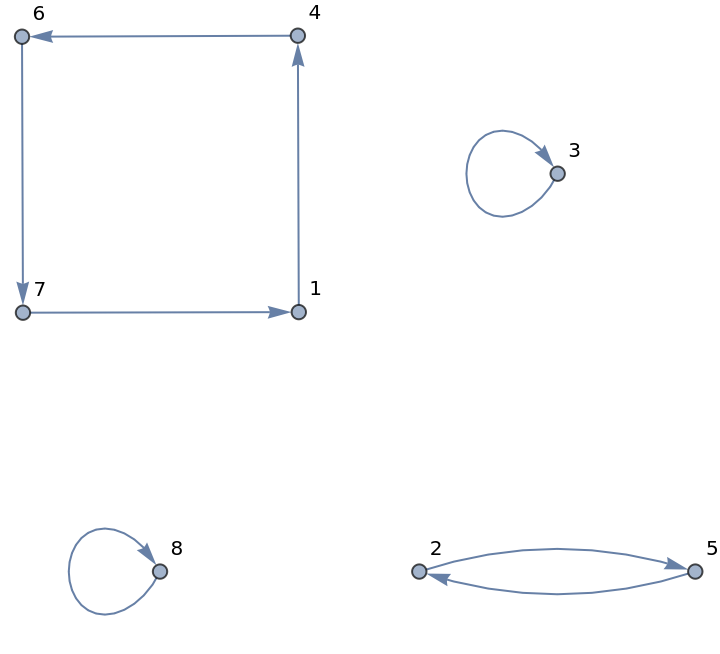
|
| In[9]:= |
|
| Out[9]= |
|
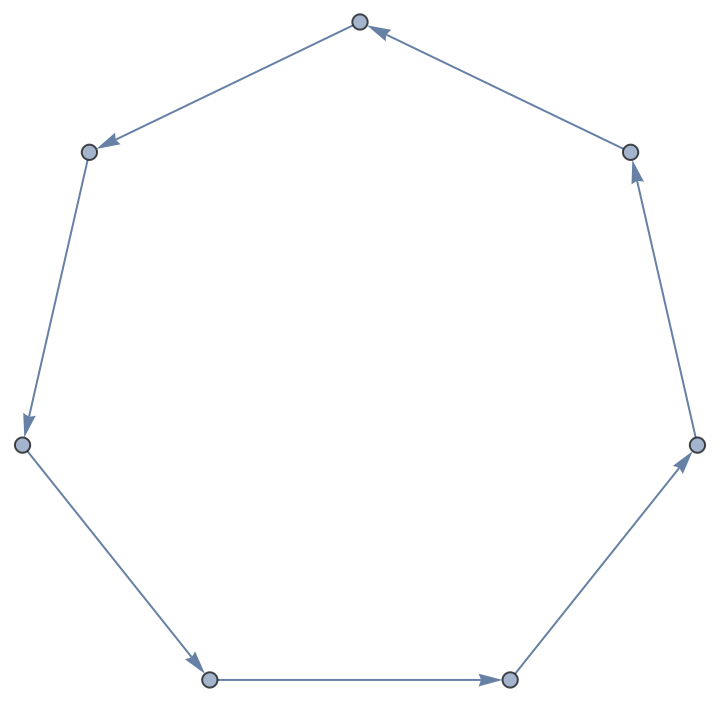
PermutationCyclesGraph of a permutation represented as cycles does not include fixed points; neither does the Cycles representation:
| In[10]:= |
|
| Out[10]= |
|
| In[11]:= |
|
| Out[11]= |
|
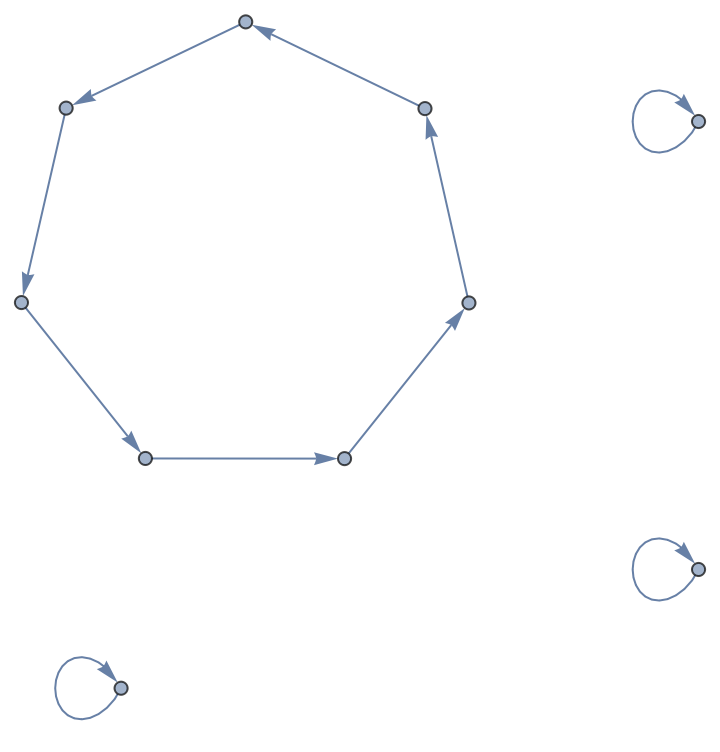
Construct a permutation list to include fixed points:
| In[12]:= |
|
| Out[12]= |
|
| In[13]:= |
|
| Out[13]= |
|
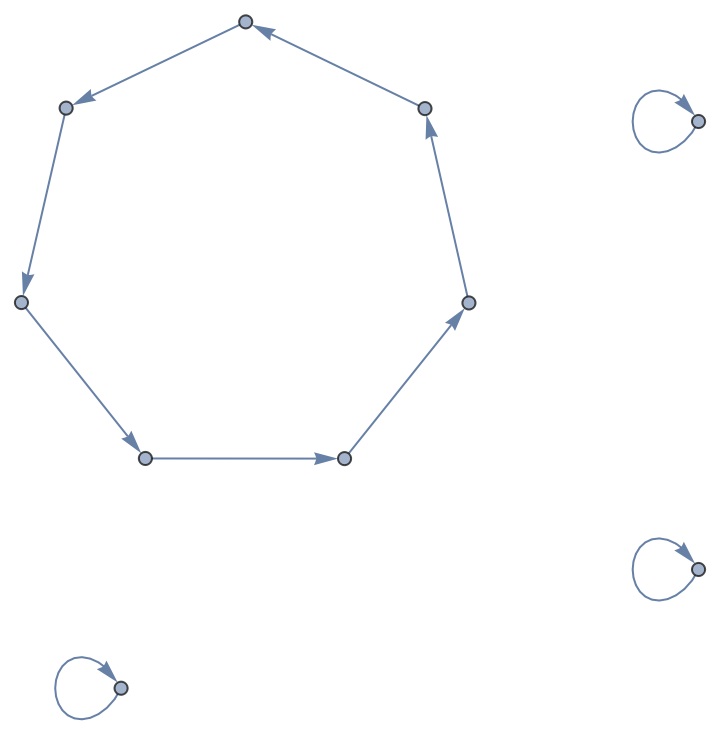
Alternatively, use an arbitrary head, rather than Cycles, when computing permutation cycles:
| In[14]:= |
|
| Out[14]= |
|
| In[15]:= |
|
| Out[15]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License