Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Test whether a graph is perfect
The GraphComplement of a perfect Graph is perfect:
| In[3]:= | ![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7}, {Null,
SparseArray[
Automatic, {7, 7}, 0, {1, {{0, 4, 6, 7, 11, 15, 19, 24}, {{4}, {5}, {6}, {
7}, {5}, {7}, {6}, {1}, {5}, {6}, {7}, {1}, {2}, {4}, {
7}, {1}, {3}, {4}, {7}, {1}, {2}, {4}, {5}, {6}}}, Pattern}]}, {VertexCoordinates -> {{1, 1}, {4, 3}, {3,
Rational[3, 2]}, {6, 1}, {3, 6}, {3, 2}, {3, 3}}}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{1., 1.}, {4., 3.}, {3., 1.5}, {6., 1.}, {3., 6.}, {3., 2.}, {3., 3.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 4}, {1, 5}, {1, 6}, {1, 7}, {2, 5}, {2, 7}, {
3, 6}, {4, 5}, {4, 6}, {4, 7}, {5, 7}, {6, 7}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.043048128342245986], DiskBox[2, 0.043048128342245986], DiskBox[3, 0.043048128342245986], DiskBox[4, 0.043048128342245986], DiskBox[5, 0.043048128342245986], DiskBox[6, 0.043048128342245986], DiskBox[7, 0.043048128342245986]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\);](https://www.wolframcloud.com/obj/resourcesystem/images/9ae/9aea58e4-e9d6-4565-9de8-b41772f486a2/727381a95a2db6e1.png) |
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= | 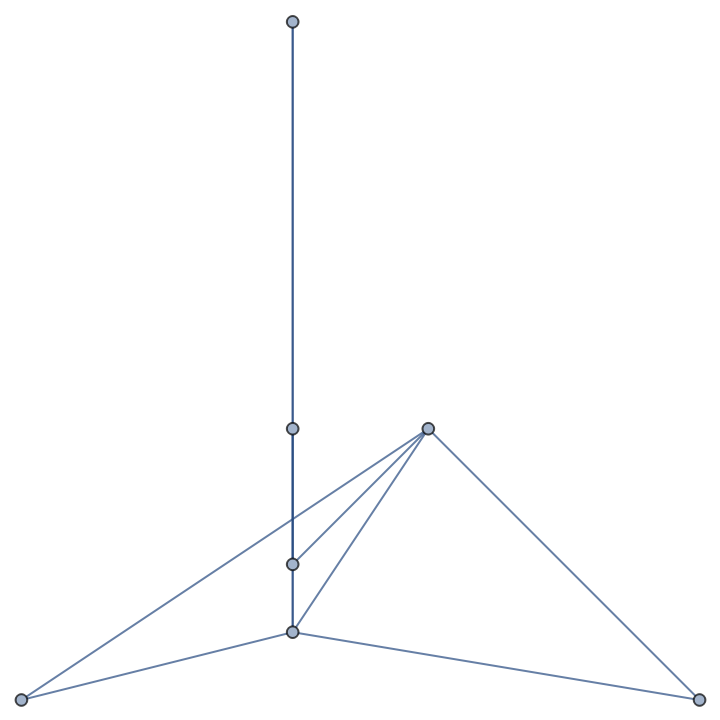 |
| In[6]:= |
| Out[6]= |
If the graph complement of g is imperfect, then so is g:
| In[7]:= | ![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6}, {Null,
SparseArray[
Automatic, {6, 6}, 0, {1, {{0, 3, 6, 9, 11, 13, 16}, {{3}, {4}, {6}, {4}, {
5}, {6}, {1}, {5}, {6}, {1}, {2}, {2}, {3}, {1}, {2}, {
3}}}, Pattern}]}, {VertexCoordinates -> {{
Rational[
1, 2], Rational[-1, 2] (
1 + 2 5^Rational[-1, 2])^Rational[1, 2]}, {0, (
Rational[1, 10] (5 + 5^Rational[1, 2]))^Rational[
1, 2]}, {
Rational[-1, 2], Rational[-1, 2] (1 + 2 5^Rational[-1, 2])^Rational[
1, 2]}, {Rational[1, 4] (1 + 5^Rational[1, 2]), Rational[
1, 2] (Rational[1, 10] (5 - 5^Rational[1, 2]))^Rational[
1, 2]}, {Rational[1, 4] (-1 - 5^Rational[1, 2]), Rational[
1, 2] (Rational[1, 10] (5 - 5^Rational[1, 2]))^Rational[
1, 2]}, {0, 0}}}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{0.5, -0.6881909602355868}, {0., 0.85065080835204}, {-0.5, -0.6881909602355868}, {
0.8090169943749475, 0.2628655560595668}, {-0.8090169943749475, 0.2628655560595668}, {0., 0.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 3}, {1, 4}, {1, 6}, {2, 4}, {2, 5}, {2, 6}, {
3, 5}, {3, 6}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.019434941751084317], DiskBox[2, 0.019434941751084317], DiskBox[3, 0.019434941751084317], DiskBox[4, 0.019434941751084317], DiskBox[5, 0.019434941751084317], DiskBox[6, 0.019434941751084317]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\);](https://www.wolframcloud.com/obj/resourcesystem/images/9ae/9aea58e4-e9d6-4565-9de8-b41772f486a2/0484a84bad13e56b.png) |
| In[8]:= |
| Out[8]= | 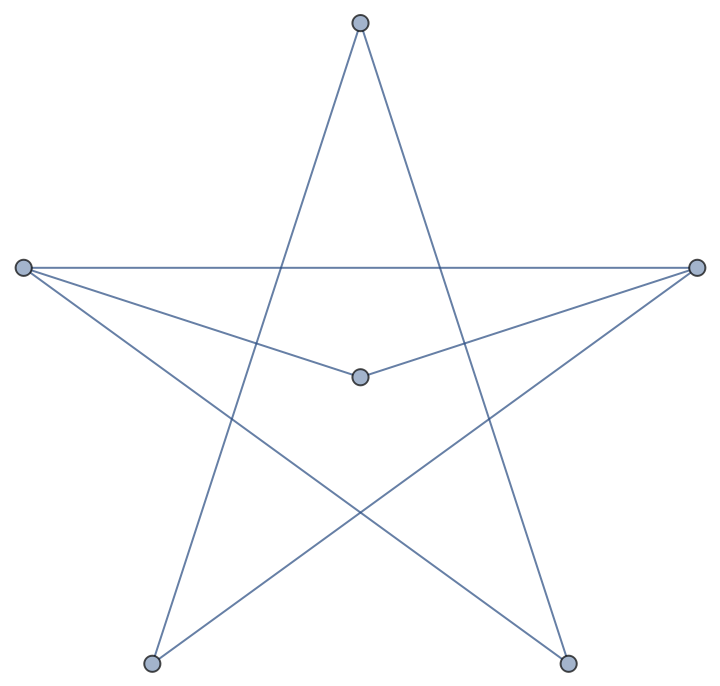 |
| In[9]:= |
| Out[9]= |
Bipartite graphs are perfect:
| In[10]:= | ![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {Null,
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 3, 6, 9, 12, 15, 18, 21, 24}, {{2}, {3}, {5}, {
1}, {4}, {6}, {1}, {4}, {7}, {2}, {3}, {8}, {1}, {6}, {
7}, {2}, {5}, {8}, {3}, {5}, {8}, {4}, {6}, {7}}}, Pattern}]}, {VertexCoordinates -> {{-0.333, -0.333}, {-1., -1.}, {-0.333, 0.333}, {-1., 1.}, {0.333, -0.333}, {1., -1.}, {
0.333, 0.333}, {1., 1.}}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
LineBox[{{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}, {
DynamicLocation[
"VertexID$1", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}, {
DynamicLocation[
"VertexID$1", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$3", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}, {
DynamicLocation[
"VertexID$4", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}, {
DynamicLocation[
"VertexID$6", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$7", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
DiskBox[{-0.333, -0.333}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
DiskBox[{-1., -1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{-0.333, 0.333}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{-1., 1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{0.333, -0.333}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
DiskBox[{1., -1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$6"],
TagBox[
DiskBox[{0.333, 0.333}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$7"],
TagBox[
DiskBox[{1., 1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$8"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{0.9999999999999911, 98.99999999999999}, {-50.92, 47.08}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
ImageSize->100]\);](https://www.wolframcloud.com/obj/resourcesystem/images/9ae/9aea58e4-e9d6-4565-9de8-b41772f486a2/113c459bbfdf65e3.png) |
| In[11]:= |
| Out[11]= |
Line graphs of bipartite graphs are perfect:
| In[12]:= | ![LineGraph[\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {Null,
SparseArray[
Automatic, {8, 8}, 0, {1, {{0, 3, 6, 9, 12, 15, 18, 21, 24}, {{2}, {3}, {5}, {
1}, {4}, {6}, {1}, {4}, {7}, {2}, {3}, {8}, {1}, {6}, {
7}, {2}, {5}, {8}, {3}, {5}, {8}, {4}, {6}, {7}}}, Pattern}]}, {VertexCoordinates -> {{-0.333, -0.333}, {-1., -1.}, {-0.333, 0.333}, {-1., 1.}, {0.333, -0.333}, {1., -1.}, {0.333, 0.333}, {1., 1.}}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
LineBox[{{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}, {
DynamicLocation[
"VertexID$1", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}, {
DynamicLocation[
"VertexID$1", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$3", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}, {
DynamicLocation[
"VertexID$4", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}, {
DynamicLocation[
"VertexID$6", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$7", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
DiskBox[{-0.333, -0.333}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
DiskBox[{-1., -1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{-0.333, 0.333}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{-1., 1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{0.333, -0.333}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
DiskBox[{1., -1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$6"],
TagBox[
DiskBox[{0.333, 0.333}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$7"],
TagBox[
DiskBox[{1., 1.}, 0.02261146496815286], "DynamicName", BoxID -> "VertexID$8"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{0.9999999999999911, 98.99999999999999}, {-50.92, 47.08}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
ImageSize->100]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/9ae/9aea58e4-e9d6-4565-9de8-b41772f486a2/00a89a3a652d69a8.png) |
| Out[12]= |  |
| In[13]:= |
| Out[13]= |
Interval graphs (and chordal graphs in general) are perfect:
| In[14]:= | ![ResourceFunction["IntervalGraph"][{Interval[{1, 6}], Interval[{2, 4}],
Interval[{3, 11}], Interval[{5, 10}], Interval[{7, 8}], Interval[{9, 13}], Interval[{12, 14}]}, VertexLabels -> "Name", GraphLayout -> "CircularEmbedding"]](https://www.wolframcloud.com/obj/resourcesystem/images/9ae/9aea58e4-e9d6-4565-9de8-b41772f486a2/62a51f1a27f4cc40.png) |
| Out[15]= | 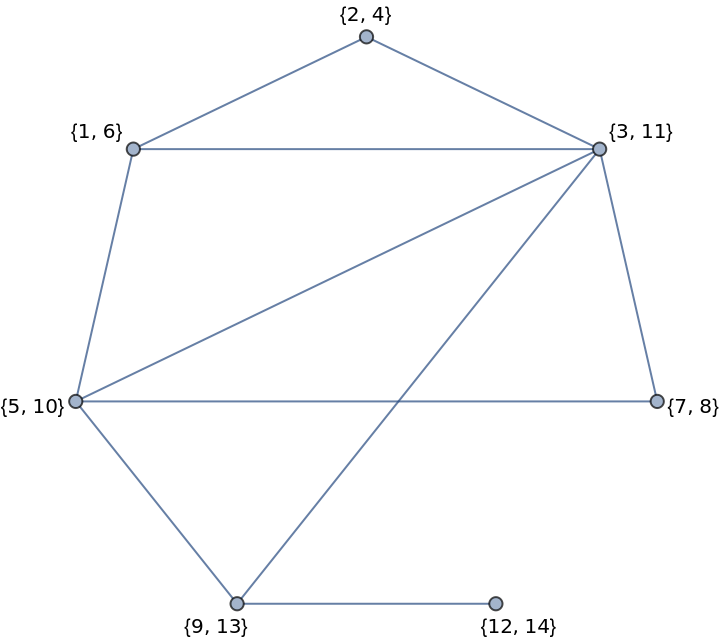 |
| In[16]:= |
| Out[16]= |
For named graphs, you can check the "Perfect" and "Imperfect" properties within GraphData without computing PerfectGraphQ:
| In[17]:= |
| Out[17]= | 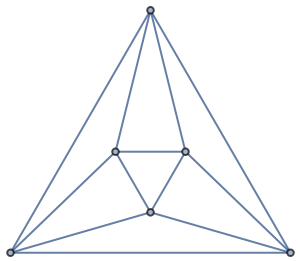 |
| In[18]:= |
| Out[18]= |
| In[19]:= |
| Out[19]= |
| In[20]:= |
| Out[20]= |
This work is licensed under a Creative Commons Attribution 4.0 International License