Basic Examples (2)
Partition a list of integers by imposing a condition on their Total:
Partition a list of random strings by a condition on their ByteCount:
Scope (4)
Partition a list of numbers by any logical condition:
Verify the totals:
Partition a list of natural numbers so each partition adds up to a prime number:
The totals are all prime:
Create partitions containing two prime values each:
Partition a text by a condition on some Characters in it:
Select substrings until there are three "a" characters in each:
Options (6)
ShortestPartitions (6)
By default, the splitting of the original list happens as soon as the Shortest possible partition is found:
It is also possible to search, for each element, the Longest possible partition until the end of the list:
However, with this option the partition algorithm becomes essentially quadratic and inefficient on a large scale:
A possible middle ground can sometimes be found by setting the option "ShortestPartitions" to an integer k >= 2, to search a longer partition k-1 elements after the shortest is found:
This effectively implements a (Monte Carlo) randomized algorithm, that is often correctly reproducing the longest partitions in an always efficient way:
In any case, the different k-next-to-shortest partitions can be of independent interest:
Applications (4)
The following list of data (scraped from arXiv) has very irregular element sizes:
If you try to upload a too large Partition of it unto a Databin, you may exceed the size limits:
An optimal partition can be found instead through PartitionWhile[list,ByteCount[#]<=n&]:
The DatabinUpload is now successful:
Properties and Relations (5)
PartitionWhile[list,Length[#]<=n&] is equivalent Partition[list,UpTo[n]]:
PartitionWhile[list,Apply[SameQ,#]&] is equivalent Split[list]:
In some cases (but see the comments in Possible Issues), PartitionWhile[list,Apply[SameQ,f[#]]&] is equivalent to SplitBy[list,f]:
In many cases, the output of PartitionWhile[list,fun] is equivalent to that of the built-in SequenceCases, but it implements a significantly faster algorithm:
In some cases, the output of PartitionWhile[list,fun] is different from SequenceCases, because of a different criterion for sequence splitting:
The output of SequenceCases can be always recovered by setting the option "ShortestPartitions" to False:
Possible Issues (2)
Only partitions for conditions evaluating to True are returned:
So if the condition is always evaluated to False, you can use its contrary:
Compare with SplitBy:
Similarly, when the condition is evaluated sometimes to True and sometimes to False, only the former cases are returned:
The different behaviour of SplitBy can then be reproduced as follows:
Neat Examples (2)
Take the low level definition code and generate a much faster compiled version:
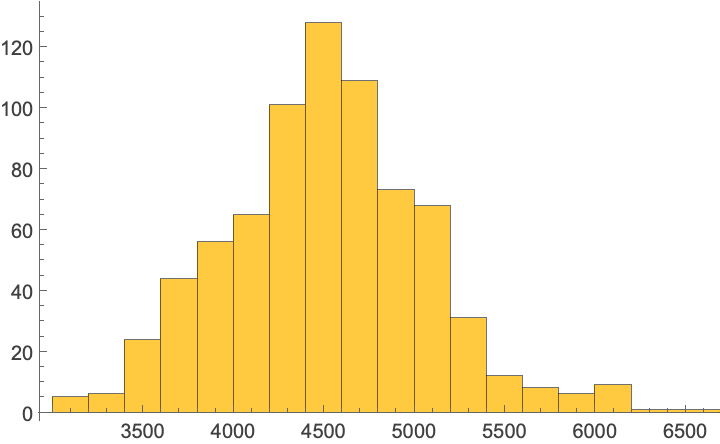
Compare the performance with the uncompiled version and the built-in SequenceCases:




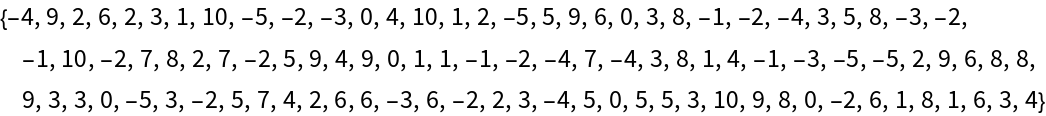
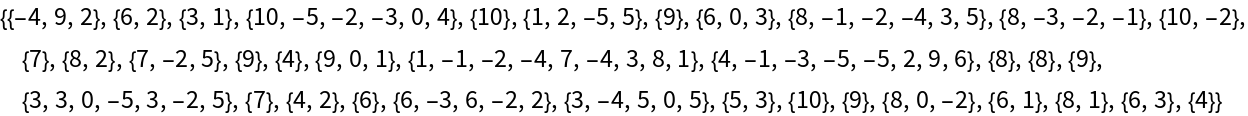


![Block[{max = 12, lenL, diff},
lenL = Flatten[Table[
Comap[{Map[Length, #] &}, ResourceFunction["PartitionWhile"][integers, Total[#] <= 10 &, "ShortestPartitions" -> n]], {n, 1, max}], 1];
(*Print[Grid@DeleteDuplicates@lenL];*)
diff = Table[If[
lenL[[i]] != lenL[[i + 1]], {i + 1, Diff[lenL[[i]], lenL[[i + 1]], "Combined"]}, Nothing], {i, 1, max - 1}];
Prepend[diff, Style[#, Bold] & /@ {"k-Shortest", "lengths Diff"}]] // Grid](https://www.wolframcloud.com/obj/resourcesystem/images/f6a/f6a8a4bb-3c99-45ea-ac80-ec867556c09d/6ae471939e2d9d6b.png)





![pwlTot[list_] := With[{fun = Total[#] <= 1000 &},
Block[{len, i, j, first, last, elq, prtind}, len = Length[list]; prtind = {}; For[i = 1, i <= len, i++, first = i;
last = 0; For[j = i, j <= len, j++, elq = fun[list[[i ;; j]]];
If[elq,
last = j,
If[last != 0, Break[]]]]; If[last != 0,
i = last;
AppendTo[prtind, {first, last}]]]; Map[Take[list, #] &, prtind]]]](https://www.wolframcloud.com/obj/resourcesystem/images/f6a/f6a8a4bb-3c99-45ea-ac80-ec867556c09d/15b8189f6eac30e1.png)
![pwlTotComp =
FunctionCompile[Function[ Typed[arg, "NumericArray"::["MachineInteger", 1]], Typed[
DownValuesFunction[pwlTot],
{"NumericArray"::["MachineInteger", 1]} -> "NumericArray"::["MachineInteger", 2]]
[arg]]]](https://www.wolframcloud.com/obj/resourcesystem/images/f6a/f6a8a4bb-3c99-45ea-ac80-ec867556c09d/13507ed60fe6395a.png)