Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
List all possible partitions of a list into disjoint pairs
ResourceFunction["ParityPairings"][items] lists all partitionings of items into disjoint pairs matching each single item once to any other or to itself. |
The only pairing of one item is the Identity:
| In[1]:= |
| Out[1]= |
Two items admit two distinct pairings:
| In[2]:= |
| Out[2]= |
Alternatively, items can also be entered as integers:
| In[3]:= |
| Out[3]= |
Compare with the result of the resource function Involutions:
| In[4]:= | ![Function[{ind}, SameQ[ResourceFunction["ParityPairings"][Range[ind]],
Map[Sort, ResourceFunction["Involutions"][ind, "Cycles"] /. {x_Integer} :> {x, x}, {0, 1}]
]] /@ Range[10]](https://www.wolframcloud.com/obj/resourcesystem/images/0d4/0d42fa4e-d7a8-4790-9e1e-0c700ee4afcb/239b3c65b1e3089d.png) |
| Out[4]= |
Plot the relative time savings:
| In[5]:= | ![ListPlot[
Function[{ind}, Divide[
2 Apply[Subtract, #],
Apply[Plus, #]
] &@{AbsoluteTiming[
ResourceFunction["Involutions"][ind, "Cycles"]][[1]],
AbsoluteTiming[
ResourceFunction["ParityPairings"][Range[ind]]][[1]] }] /@ Range[10], PlotRange -> {0, 2}]](https://www.wolframcloud.com/obj/resourcesystem/images/0d4/0d42fa4e-d7a8-4790-9e1e-0c700ee4afcb/6015a539c6ec8c67.png) |
| Out[5]= | 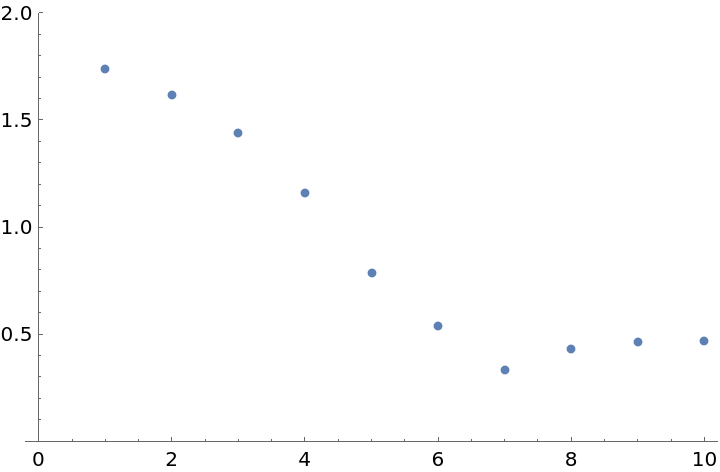 |
Count the number of distinct involutions on n letters (cf. OEIS A000085):
| In[6]:= |
| Out[6]= |
This work is licensed under a Creative Commons Attribution 4.0 International License