Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ParetoListMinima

Source Notebook

Find the Pareto-minimal points in a set of numeric vectors

Contributed by: Daniel Lichtblau

ResourceFunction["ParetoListMinima"][points]

gives the subset of points that are Pareto-minimal.

Details and Options

Given a set of real-valued points in n-dimensional space, a point p={p1,…,pn} is defined to be Pareto-minimal if no other point in the set q={q1,…,qn} has q1≤pi for all 1≤i≤n.
Pareto-minima are minimal elements with respect to the partial ordering induced by component-wise less-or-equal comparisons.
ResourceFunction["ParetoListMinima"] uses the Bentley-Clarkson-Levine algorithm.
The result can have points in a different order from their relative positioning in the input.

Examples

Basic Examples (1) 

Find the Pareto minima of five points in 3D:

In[1]:=
ResourceFunction[ "ParetoListMinima"][{{1, 2, 3}, {4, 5, 6}, {3, 1, 8}, {1, 9, 3}, {2, 3, 2}}]
Out[1]=

Scope (4) 

Create a list of 20 random integer vectors in 3D:

In[2]:=
SeedRandom[1234]; pts = RandomInteger[{1, 10}, {20, 3}]
Out[3]=

Compute the Pareto minima for this set:

In[4]:=
ResourceFunction["ParetoListMinima"][pts]
Out[4]=

Compute the Pareto minima for a set of 200 points in 2D:

In[5]:=
SeedRandom[1234]; pts = RandomReal[{1, 10}, {200, 2}]; mins = ResourceFunction["ParetoListMinima"][pts]; nonmins = DeleteCases[pts, Alternatives @@ mins]; {Length[mins], Length[nonmins]}
Out[9]=

Show the Pareto minima connected by segments, along with the other points:

In[10]:=
Show[{ListPlot[Style[SortBy[mins, First], Green], Joined -> True], ListPlot[Style[SortBy[mins, First], Red]], ListPlot[nonmins]}, PlotRange -> All, AxesOrigin -> 0]
Out[10]=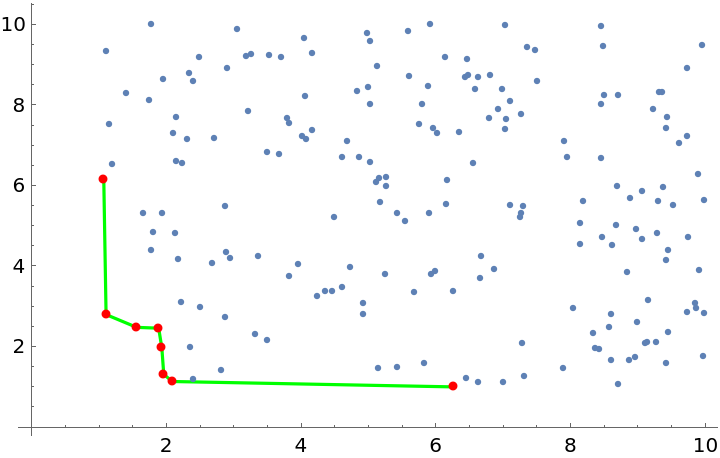

Pareto-maximal points are defined in the same way as minimal points, except using GreaterEqual as the component-wise inequality. One can use ParetoListMinima in a simple way to compute the Pareto-maximal points:

In[11]:=
ParetoListMaxima[list_] := -ResourceFunction["ParetoListMinima"][-list] SeedRandom[1234]; pts = RandomReal[{1, 10}, {200, 2}]; maxes = ParetoListMaxima[pts]; nonmaxes = DeleteCases[pts, Alternatives @@ maxes]; {Length[maxes], Length[nonmaxes]}
Out[12]=

Show the Pareto maxima connected by segments, along with the other points:

In[13]:=
Show[{ListPlot[Style[SortBy[maxes, First], Green], Joined -> True], ListPlot[Style[SortBy[maxes, First], Red]], ListPlot[nonmaxes]}, PlotRange -> All, AxesOrigin -> 0]
Out[13]=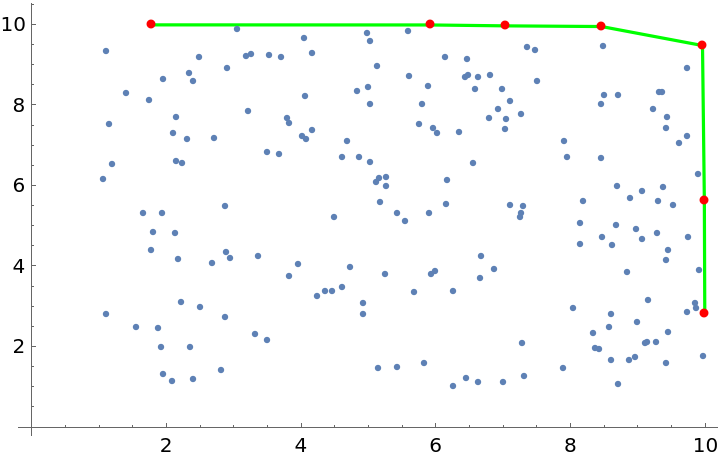

Compute Pareto minima for 200 points in 3D:

In[14]:=
SeedRandom[1234]; pts = RandomReal[{1, 10}, {200, 3}]; mins = ResourceFunction["ParetoListMinima"][pts]; nonmins = DeleteCases[pts, Alternatives @@ mins]; {Length[mins], Length[nonmins]}
Out[18]=

Show the Pareto maxima, the planar mesh they define, and the non-minima above them:

In[19]:=
Show[{ListPointPlot3D[Style[mins, Green]], ListPlot3D[mins, PlotStyle -> None], ListPointPlot3D[nonmins]}, PlotRange -> All, AxesOrigin -> 0]
Out[19]=

Version History

  • 1.0.0 – 24 April 2020

Related Resources

License Information