Function Repository Resource:

ParenthesesTrees

Obtain a list of syntax trees consistent with a valid pattern of parentheses

Contributed by: Bradley Klee

ResourceFunction["ParenthesesTrees"][str]

lists valid syntax trees for reading pairs of parentheses from the input string str.

Details

Every valid input is a string containing only equal numbers of open and close parentheses characters, "(" and ")". Additionally, when reading left to right, the count of "(" must always equal or exceed the count of ")". For example, neither "({})" nor "()())(" are valid, while "(()(()))" is valid.

Valid inputs are read into trees according to a grammar found in the notes of New Kind of Science:

"()" → x_i

x_i=Tree[Null,{"(",")"}]

"(x_j)" → x_k

x_k=Tree[Null,{"(",x_j,")"}]

continue

"x_mx_n" → x_p

x_p=Tree[Null,{x_m,x_n}]

combine

The third rule for combining groups of characters is not uniquely applicable when three or more x_i terms occur directly in sequence. Consequently most inputs have more than one valid interpretation as a syntax tree.

ParenthesisTree takes the same options as Tree, and uniformly applies those options to all trees returned.

ParenthesisTree also allows for a custom TreeLayout, called "SerializedLeaves", which puts leaves in a left-to-right order and sets TreeElementCoordinates to make the serial ordering more obvious.

Examples

Basic Examples (4)

There is only one parenthesis tree with two leaves:

In[1]:=

Out[1]=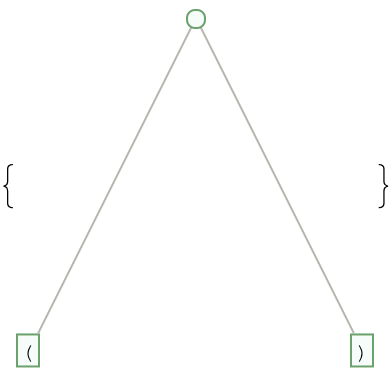

The smallest input with non-unique output has three pairs of open-close parentheses:

In[2]:=

Out[2]=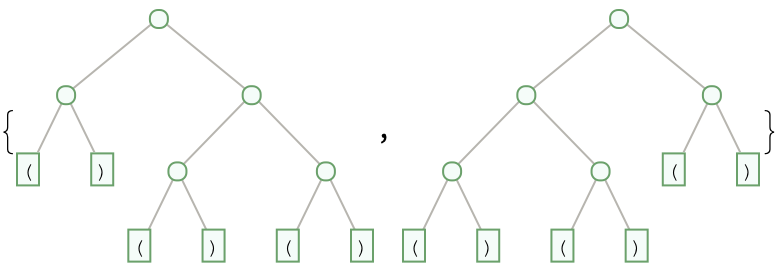

It's not too difficult to find ever-larger inputs with unique syntax trees:

In[3]:=

Out[3]=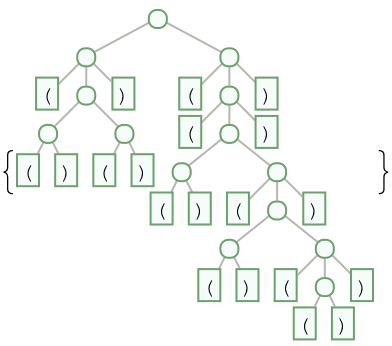

It's also easy to find larger inputs with many equivalent syntax trees:

In[4]:=

Out[4]=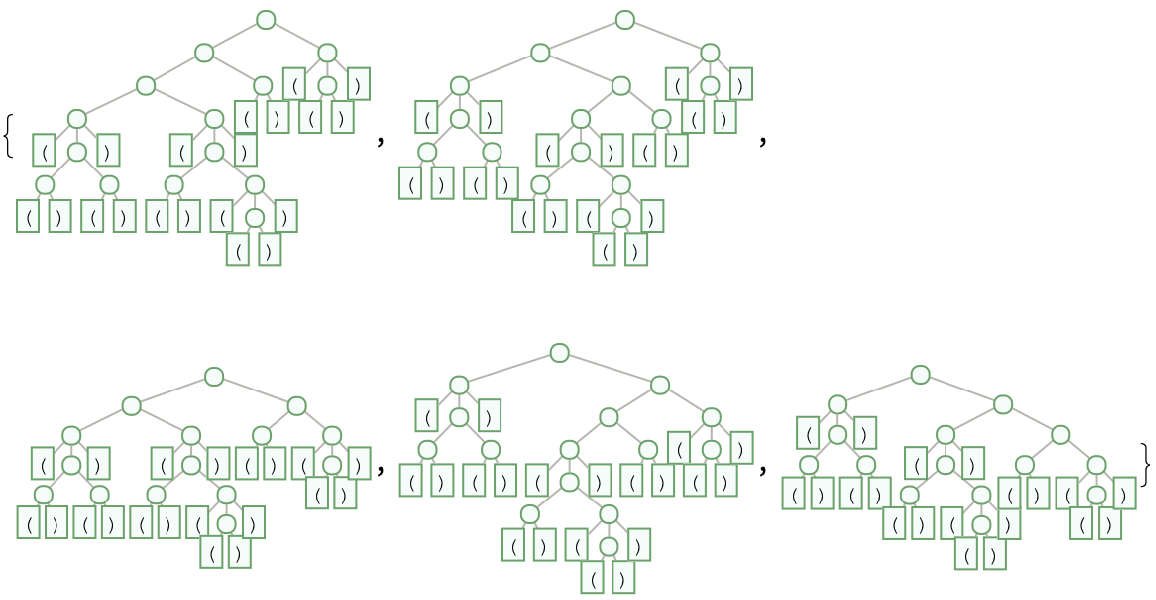

Scope (1)

The Null string is uniquely interpreted as a tree consisting only of a root node:

In[5]:=

Out[5]=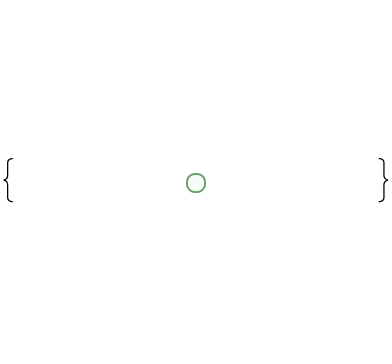

Options (2)

Using the option setting TreeLayout→"SerializedLeafs" causes ParenthesesTrees to use a unique layout, making leaves easier to read across:

In[6]:=

Out[6]=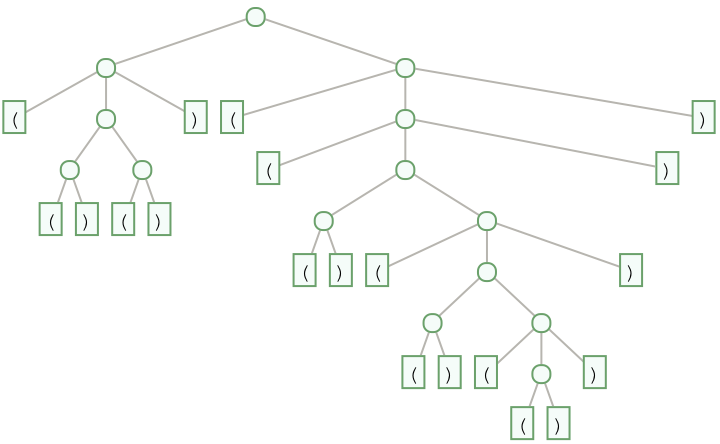

The "SerializedLeafs" layout also works with AspectRatio:

In[7]:=

Out[7]=

Neat Examples (2)

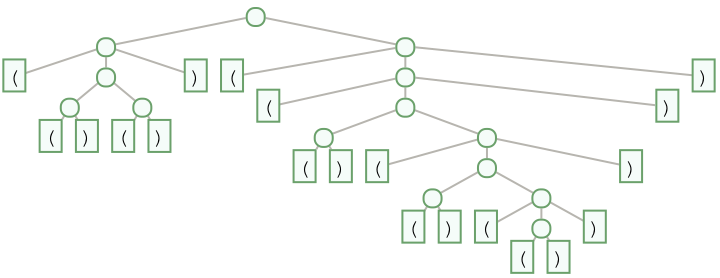Enumerate valid inputs up to length 14 and count them:

In[8]:=

$CatalanStrings[ind_] := Map[StringJoin, ReplaceAll[ Select[Permutations[Catenate[ ConstantArray[#, ind] & /@ {1, -1}]], AllTrue[Accumulate[#], # >= 0 &] &], {1 -> "(", -1 -> ")"}]]$