Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the integral of an expression involving parameters, returning a piecewise result correct for all specializations of the parameters
ResourceFunction["ParameterizedFunctionIntegrate"][f,x] gives the indefinite integral | |
ResourceFunction["ParameterizedFunctionIntegrate"][f,{x,xmin,xmax}] gives the definite integral | |
ResourceFunction["ParameterizedFunctionIntegrate"][f,{x,xmin,xmax},{y,ymin,ymax}] gives the definite integral | |
ResourceFunction["ParameterizedFunctionIntegrate"][f,{x,y,…}∈reg] integrates over the geometric region reg. |
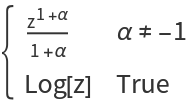 rather than the bare
rather than the bare | Assumptions | $Assumptions | assumptions to make about parameters |
| GenerateConditions | True | whether to generate answers that involve conditions on parameters |
| "MostGeneralFirstQ" | True | whether to attempt to order the most generic case first in Piecewise results |
| "ParameterTreatment" | "Comprehensive" | how to treat free symbolic parameters of the integrand |
| PrincipalValue | False | whether to find Cauchy principal values |
| "SubtaskTimeLimit" | 4.0 | the maximum time in seconds allotted for individual integration sub-tasks |
| "TrueInPiecewiseMeans" | None | whether to Print a user assistance mesage describing the True case in Piecewise results |
| All | return all possible answers using Piecewise |
| Automatic | return a condition only if it is not generically satisfied |
| True | return any condition that is needed |
| False | never return any needed conditions |
| None | return unevaluated if conditions are needed |
| "Generic" | directly returns the result of Integrate | |
| "Conditional" | returns an expression indicating which specializations of a generic antiderivative are valid | |
| "Comprehensive" | returns a Piecewise function that is valid for all combinations of parameter values | |
| "Continuous" | attempts to return a Piecewise result that is maximally continuous | |
| "ApartContinuous" | makes the presence of an intentionally-introduced constant more obvious as a separate term |
Compute the indefinite integral of a trigonometric function containing the parameter a:
| In[1]:= |
|
| Out[1]= |
|
Contrast with the generic result returned by Integrate:
| In[2]:= |
|
| Out[2]= |
|
A typical incorrect specialization of a generic formula:
| In[3]:= |
|
| Out[4]= |
|
but, with σ=0:
| In[5]:= |
|
| Out[5]= |
|
Pre-substitution shows that the original integral was well defined:
| In[6]:= |
|
| Out[6]= |
|
Get the comprehensize Piecewise result, correct for all values of α:
| In[7]:= |
|
| Out[7]= |
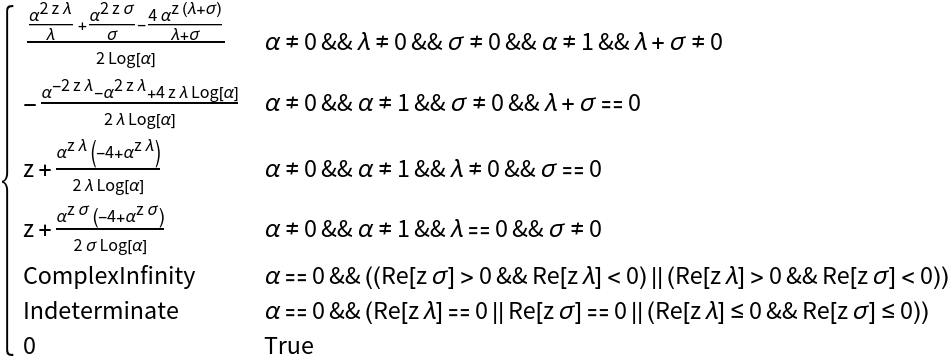
|
Compute a definite integral:
| In[8]:= |
|
| Out[8]= |
|
Perform an integral over a Region in the {x,y} plane:
| In[9]:= |
|
| Out[9]= |
|
For certain "ParameterTreatment" settings, ParameterizedFunctionIntegrate will return conditions on parameters that ensure convergence:
| In[10]:= |
|
| Out[10]= |
|
With Assumptions, a result valid under the given assumptions is returned:
| In[11]:= |
|
| Out[11]= |
|
It is generally more appropriate and effective to use Assuming[assump,ParameterizedFunctionIntegrate[…]] rather than ParameterizedFunctionIntegrate[…,Assumptions→assump], as the latter only applies assumptions when computing a generic antiderivative with Integrate, while the former applies assumptions at all stages of the computation.
For certain "ParameterTreatment" settings, ParameterizedFunctionIntegrate will return conditions on parameters that ensure convergence:
| In[12]:= |
|
| Out[12]= |
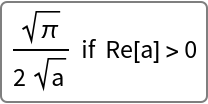
|
Use GerenateConditions→False to suppress conditions in these cases:
| In[13]:= |
|
| Out[13]= |
|
The GenerateConditions option is only effectual when the "ParameterTreatment" option is set to "Generic" or "Conditional".
GenerateConditions→False can speed up integration:
| In[14]:= |
|
| Out[14]= |
|
| In[15]:= |
|
| Out[15]= |
|
By default, the first clause in Piecewise results returned by ParameterizedFunctionIntegrate is the one that applies most generically with respect to specializaiton of parameter values:
| In[16]:= |
|
| Out[16]= |
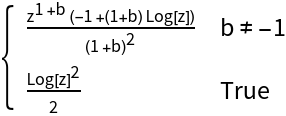
|
The opposite ordering, with the most generic clause given last, can be obtained using MostGeneralFirstQ→False. This gives predicates that may be easier to understand at a glance:
| In[17]:= |
|
| Out[17]= |
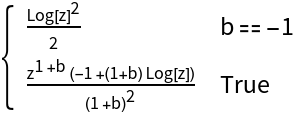
|
Using "ParameterTreatment" → "Generic" gives the most generic result, equivalent to the result of Integrate:
| In[18]:= |
|
| Out[18]= |
|
However, this generic antiderivative quietly returns an incorrect antiderivative when later specialized to α → -1:
| In[19]:= |
|
| Out[19]= |
|
For generic antiderivatives, substitution does not necessarily commute with integration:
| In[20]:= |
|
| Out[20]= |
|
ParameterTreatment→"Conditional" attempts to indicate what specializations of a generic antiderivative are valid with ConditionalExpression:
| In[21]:= |
|
| Out[21]= |
|
The result of an invalid substitution is now more appropriately given as Undefined rather than ComplexInfinity:
| In[22]:= |
|
| Out[22]= |
|
By default, the built-in Wolfram Language Integrate already returns ConditionalExpressions when appropriate for parametric definite integrals:
| In[23]:= |
|
| Out[23]= |
|
But not in the coresponding indefinite case:
| In[24]:= |
|
| Out[24]= |
|
For antiderivatives, ParameterizedFunctionIntegrate[…,"ParameterTreatment"→"Comprehensive"] returns a Piecewise function that is valid for all combinations of parameter values. For parametric integrands, the result is often a Piecewise result wherein one of the consequents is a generic antiderivative :
| In[25]:= |
|
| Out[25]= |
|
Specialization gives a correct result for all α:
| In[26]:= |
|
| Out[26]= |
|
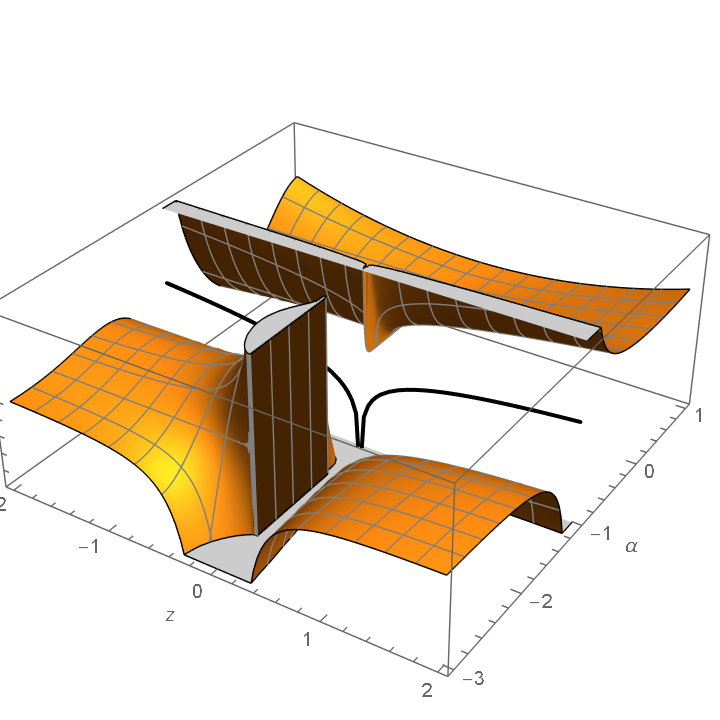
The following plot illustrates the discontinuity of this Piecewise result at the parameter value α=-1:
| In[27]:= |
![Options [plotSurfaceAndCurve] = {Exclusions -> All};
plotSurfaceAndCurve [surface_, curve_, integrationVarRange_,
parameterRange_, surfaceRange_, specialParameterRule_, options : OptionsPattern[]] :=
Show [
Plot3D [surface, integrationVarRange, parameterRange, PlotRange -> surfaceRange, AxesLabel -> {First[integrationVarRange], First [parameterRange]}, PlotPoints -> 100,
MeshStyle -> Gray,
Exclusions -> OptionValue [Exclusions]],
ParametricPlot3D[{First[integrationVarRange], Last [specialParameterRule], curve},
integrationVarRange,
PlotRange -> surfaceRange, PlotStyle -> Black,
Exclusions -> OptionValue [Exclusions]]];](https://www.wolframcloud.com/obj/resourcesystem/images/fff/fffe6e3e-f313-4a35-85ce-54f028c0736b/0e9fe996533dd0a7.png)
|
| In[28]:= |
|
| Out[28]= |
|
At the expense of more computing time, "ParameterTreatment" → "Continuous" attempts to return a Piecewise result that is maximally continuous:
| In[29]:= |
|
| Out[29]= |
|
The generic first consequent ![]() is different from the corresponding
is different from the corresponding ![]() in the generic consequent of the merely "Comprehensive" result. To verify that consequent
in the generic consequent of the merely "Comprehensive" result. To verify that consequent ![]() is valid:
is valid:
| In[30]:= |
|
| Out[30]= |
|
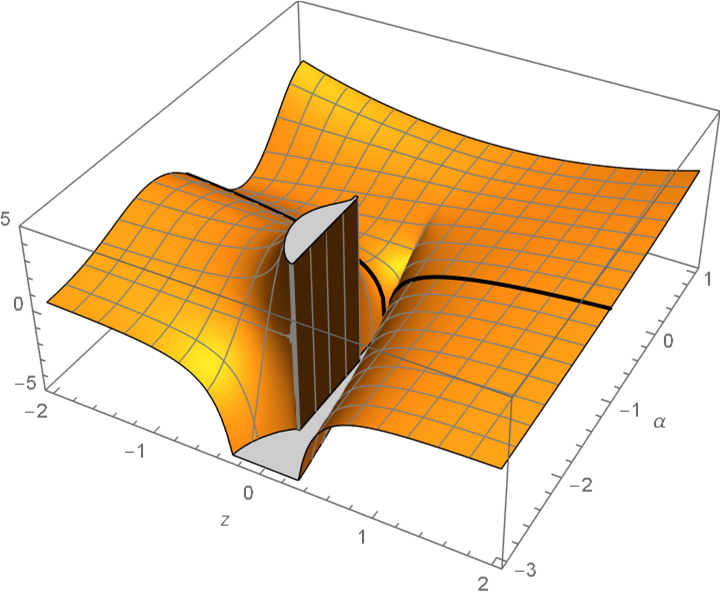
The different consequent makes the overall antiderivative continuous with respect to parameter α, as suggested by the following plot:
| In[31]:= |
![Options [plotSurfaceAndCurve] = {Exclusions -> All};
plotSurfaceAndCurve [surface_, curve_, integrationVarRange_,
parameterRange_, surfaceRange_, specialParameterRule_, options : OptionsPattern[]] :=
Show [
Plot3D [surface, integrationVarRange, parameterRange, PlotRange -> surfaceRange, AxesLabel -> {First[integrationVarRange], First [parameterRange]}, PlotPoints -> 100,
MeshStyle -> Gray,
Exclusions -> OptionValue [Exclusions]],
ParametricPlot3D[{First[integrationVarRange], Last [specialParameterRule], curve},
integrationVarRange,
PlotRange -> surfaceRange, PlotStyle -> Black,
Exclusions -> OptionValue [Exclusions]]];](https://www.wolframcloud.com/obj/resourcesystem/images/fff/fffe6e3e-f313-4a35-85ce-54f028c0736b/3729ebd6eb37a42f.png)
|
| In[32]:= |
![plotSurfaceAndCurve[Re[(-1 + z^(1 + \[Alpha]))/(1 + \[Alpha])], Re[Log[z]], {z, -2, 2}, {\[Alpha], -3, 1}, {-5, 5}, \[Alpha] -> -1, Exclusions -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/fff/fffe6e3e-f313-4a35-85ce-54f028c0736b/13cc1e10f845b030.png)
|
| Out[32]= |
|
The parametric continuity was accomplished by introducing a particular integration constant that is a function of at most the parameter alone, making its partial derivative with respect to the integration variable z vanish. Although parametric continuity is not necessary for some applications, including definite integration, see "Applications" for a differential equation example where parametric continuity is necessary.
At the expense of more time, and perhaps also more catastrophic cancellation when substituting floating-point numbers near a special case, setting "ParameterTreatment"→"ApartContinuous" will attempt to make the presence of intentionally-introduced constants more obvious in a separate term:
| In[33]:= |
|
| Out[33]= |
|
Contrast with the merely "Continuous" result:
| In[34]:= |
|
| Out[34]= |
|
Certain ordinary Riemann definite integrals are divergent:
| In[35]:= |
|
| Out[35]= |
|
By interpreting instead as a Cauchy principal value integral, we can give meaning to such cases:
| In[36]:= |
|
| Out[36]= |
|
Use "TrueInPiecewiseMeans"→ All to Print a user assistance message which expands the True predicate in Piecewise results into a condition on parameters:
| In[37]:= |
|
| Out[37]= |
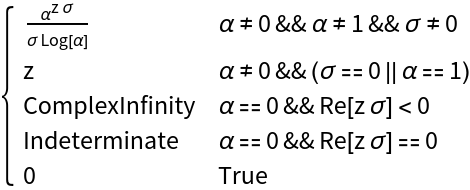
|
By default, "TrueInPiecewiseMeans"→False and no messages are printed:
| In[38]:= |
|
| Out[38]= |
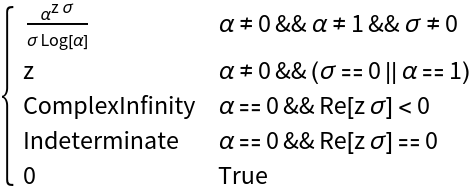
|
When "TrueInPiecewiseMeans"→ Automatic, a message is printed when the number of Piecewise clauses is greater than two:
| In[39]:= |
|
| Out[39]= |
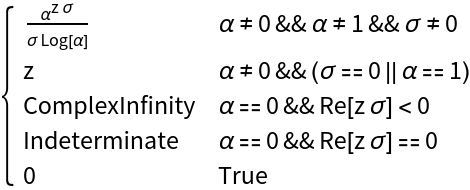
|
But not otherwise:
| In[40]:= |
|
| Out[40]= |
|
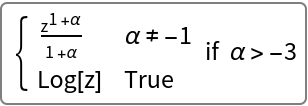
Using ParameterizedFunctionIntegrate within an enclosing Assuming returns a ConditionalExpression that might or might not contain a Piecewise result:
| In[41]:= |
![Assuming [\[Alpha] > -3, ResourceFunction["ParameterizedFunctionIntegrate"][z^\[Alpha], z, "ParameterTreatment" -> "Comprehensive"]]](https://www.wolframcloud.com/obj/resourcesystem/images/fff/fffe6e3e-f313-4a35-85ce-54f028c0736b/53cb37001a1197c8.png)
|
| Out[41]= |
|
| In[42]:= |
![Assuming [\[Alpha] > -1, ResourceFunction["ParameterizedFunctionIntegrate"][z^\[Alpha], z, "ParameterTreatment" -> "Comprehensive"]]](https://www.wolframcloud.com/obj/resourcesystem/images/fff/fffe6e3e-f313-4a35-85ce-54f028c0736b/6ef0117206161dc8.png)
|
| Out[42]= |
|
ParameterizedFunctionIntegrate is more likely to succeed and to do so quickly if wrapped in Assuming rather than doing a replacement after obtaining a more general result.
As with most Wolfram Language functions, the default domain for the integration variable and parameters is the Complexes. However, you can use Assuming to restrict the integration variable and/or parameters to the Reals:
| In[43]:= |
![Assuming [Element [z | \[Alpha], Reals], ResourceFunction["ParameterizedFunctionIntegrate"] [z^\[Alpha], z, "ParameterTreatment" -> "Comprehensive"]]](https://www.wolframcloud.com/obj/resourcesystem/images/fff/fffe6e3e-f313-4a35-85ce-54f028c0736b/4afea34637381cef.png)
|
| Out[43]= |
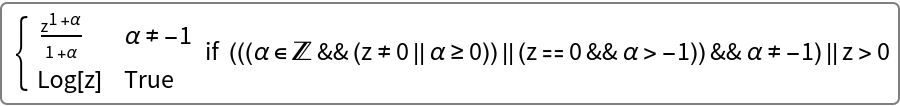
|
In contrast, for the Complexes:
| In[44]:= |
|
| Out[44]= |
|
As illustrated by this result, restricting parameters or the integration variable to the reals often results in a less concise result, and it usually requires more computing time. Since a result that is valid for the complexes is also valid for the reals, it is recommended that ParameterizedFunctionIntegrate is first used without such assumptions.
You might sometimes benefit from making some parameters be elements of the integers, particularly if they occur in exponents or in subexpressions such as Sin[nπ]. There might even be examples that benefit rather than suffer from declaring some parameters to be Booleans, Primes, Rationals or Algebraics, but for such examples, try first without assumptions because such restrictions often increase the complexity and computing time for no significant benefit.
DSolve returns generic general solutions to ordinary differential equations without boundary conditions:
| In[45]:= |
|
| Out[45]= |
|
But the specialization of the particular portion of the above generic solution for the resonance as ω → κ is incorrect:
| In[46]:= |
|
| Out[46]= |
|
We can instead compute the particular portion of the generic general solution with parametrically-continuous comprehensive antiderivatives, and a result valid at resonance is obtained. The first clause of this Piecewise result is the generic particular solution. The second clause is its specialization to the particular solution for ω = κ:
| In[47]:= |
![y1 = Cos [\[Kappa] t];
y2 = Sin[\[Kappa] t];
Wrongskian = Simplify [y1*D[y2, t] - y2*D[y1, t]];
parametricallyContinuousParticular = FullSimplify[
y2*ResourceFunction["ParameterizedFunctionIntegrate"] [(
y1 Cos[\[Omega] t])/Wrongskian, t, "ParameterTreatment" -> "Continuous"] - y1*ResourceFunction["ParameterizedFunctionIntegrate"] [(
y2 Cos[\[Omega] t])/Wrongskian, t, "ParameterTreatment" -> "Continuous"]]](https://www.wolframcloud.com/obj/resourcesystem/images/fff/fffe6e3e-f313-4a35-85ce-54f028c0736b/672bd5eca4d9d041.png)
|
| Out[6]= |

|
Using this method with the built-in Integrate misses the discontinuity at ω = κ:
| In[48]:= |
![y1 = Cos [\[Kappa] t];
y2 = Sin[\[Kappa] t];
Wrongskian = Simplify [y1*D[y2, t] - y2*D[y1, t]];
FullSimplify[
y2*Integrate [(y1 Cos[\[Omega] t])/Wrongskian, t] - y1*Integrate [(y2 Cos[\[Omega] t])/Wrongskian, t]]](https://www.wolframcloud.com/obj/resourcesystem/images/fff/fffe6e3e-f313-4a35-85ce-54f028c0736b/77235b35e41e3c30.png)
|
| Out[49]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License