Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ParallelSurface

Source Notebook

Compute the parallel surface of a surface

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["ParallelSurface"][s,r,{u,v}]

computes the parallel surface at distance r from a parametric surface s in the variables u and v.

Details and Options

A surface is parallel to another if, for each point of the first, there is a point on the second at distance r in the direction of the normal vector from that point. Each such pair will have parallel tangent planes.
A parallel surface is sometimes referred to as an offset surface.

Examples

Basic Examples (3) 

Define a catenoid surface:

In[1]:=
cat = Entity["Surface", "Catenoid"]["ParametricEquations"]
Out[1]=

Compute a parallel surface to the catenoid:

In[2]:=
ResourceFunction["ParallelSurface"][ Entity["Surface", "Catenoid"]["ParametricEquations"][1][u, v], 1, {u, v}]
Out[2]=

Plot the surface and its parallels:

In[3]:=
ParametricPlot3D[ Evaluate[{ResourceFunction["ParallelSurface"][ cat[1][u, v], -.5, {u, v}], cat[1][u, v], ResourceFunction["ParallelSurface"][ cat[1][u, v], .5, {u, v}]}], {u, 0, 2 \[Pi]}, {v, -\[Pi], \[Pi]}, BoxRatios -> {1, 1, 1}, PlotRange -> 3]
Out[3]=

Scope (2) 

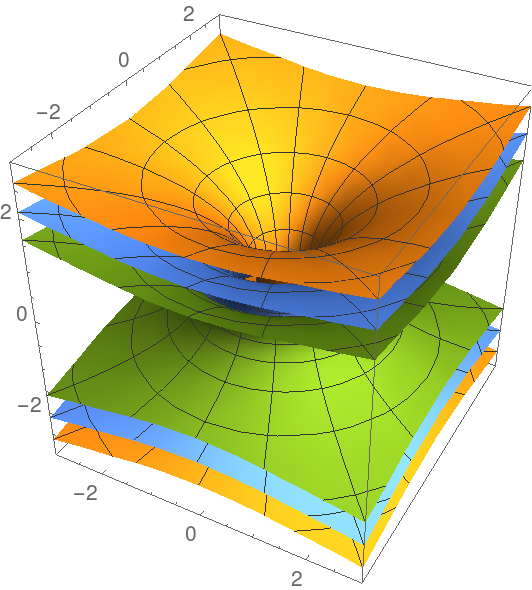Define an ellipsoid:

In[4]:=
el = Entity["Surface", "Ellipsoid"]["ParametricEquations"][3, 2, 1][u, v]
Out[4]=

Compute a parallel surface to the ellipsoid:

In[5]:=
ResourceFunction["ParallelSurface"][ Entity["Surface", "Ellipsoid"]["ParametricEquations"][3, 2, 1][u, v], r, {u, v}]
Out[5]=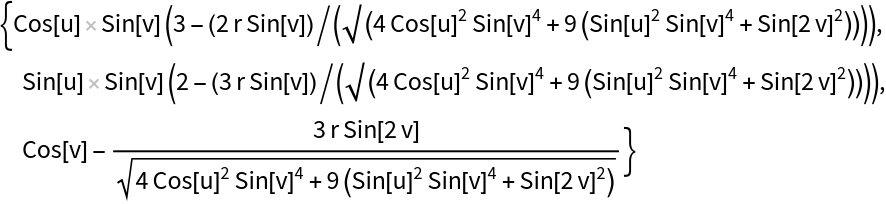

Plot the surface and its parallels with a cross section view:

In[6]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/2acc8af6-d1df-4aa8-8bd5-c343fb6c0653"]
Out[6]=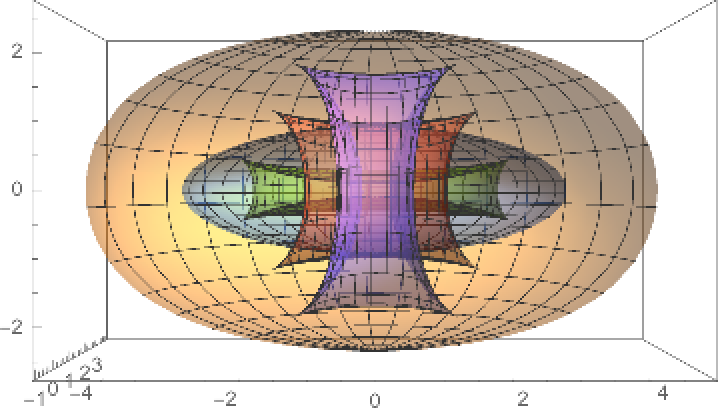

Define a Möbius strip surface:

In[7]:=
Entity["Surface", "MoebiusStrip"]["ParametricEquations"]
Out[7]=

Compute a parallel surface to the Möbius strip:

In[8]:=
ms = ResourceFunction["ParallelSurface"][ Entity["Surface", "MoebiusStrip"]["ParametricEquations"][1][u, v], r, {u, v}]
Out[8]=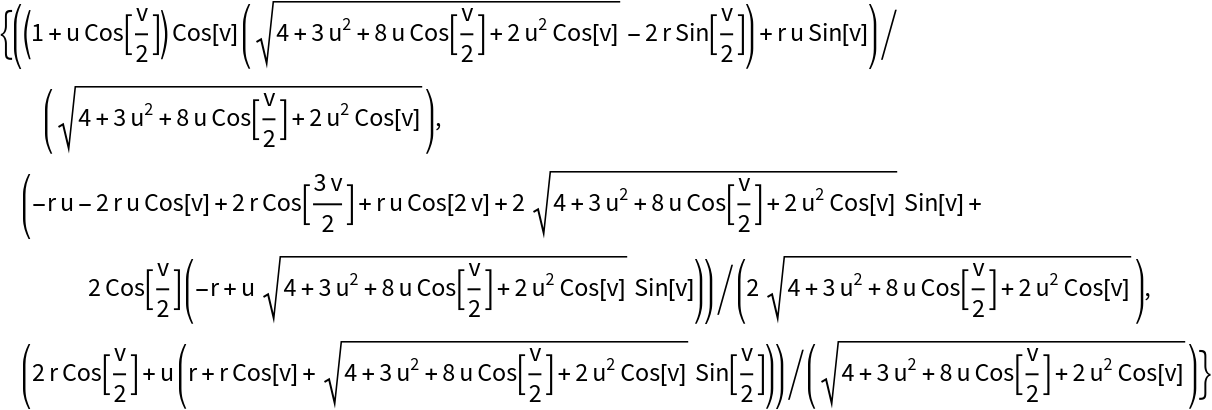

Plot the Möbius strip and a surface parallel to it, varying distance:

In[9]:=
Manipulate[ ParametricPlot3D[ Evaluate[{Entity["Surface", "MoebiusStrip"]["ParametricEquations"][ 1][u, v], ResourceFunction["ParallelSurface"][ Entity["Surface", "MoebiusStrip"]["ParametricEquations"][1][u, v], r, {u, v}]}], {u, -.5, .5}, {v, -2 \[Pi], 2 \[Pi]}, MaxRecursion -> 3, BoxRatios -> {1, 1, 1}, PlotRange -> All], {{r, 1.}, 0., 2.}]
Out[9]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 26 February 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information