Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ParallelLineThrough

Source Notebook

Compute properties of the line parallel to a given line and passing through a given point

Contributed by: Wolfram|Alpha Math Team

ResourceFunction["ParallelLineThrough"][expr,{x,a},{y,b}]

returns an Association of properties for the line passing through the point {x,y}={a,b} and parallel to expr, a linear function in x.

ResourceFunction["ParallelLineThrough"][expr,{x,a},{y,b},prop]

returns the parallel line property prop.

Details

Allowed values of prop are:
"SlopeInterceptEquation"equation of the parallel line in slope-intercept form
"StandardFormEquation"equation of the parallel line in standard form
"PointSlopeEquation"equation of the parallel line in point-slope form
"Slope"slope of the parallel line
"HorizontalIntercept"horizontal intercept of the parallel line
"VerticalIntercept"vertical intercept of the parallel line
"Plot"plot of the parallel line
AllAssociation of all allowed properties
If expr does not have head Equal, then expr is treated as an expression defining y in terms of x. In other words, ResourceFunction["ParallelLineThrough"][expr,{x,a},y,…] is equivalent to ResourceFunction["ParallelLineThrough"][y==expr,{x,a},y,…] if expr has a head other than Equal.

Examples

Basic Examples (2) 

Get the point-slope equation of a line parallel to y=5x that passes through the point (x,y)=(3,4):

In[1]:=
ResourceFunction["ParallelLineThrough"][ 5 x, {x, 3}, {y, 4}, "PointSlopeEquation"]
Out[1]=

Visualize this result:

In[2]:=
ResourceFunction["ParallelLineThrough"][5 x, {x, 3}, {y, 4}, "Plot"]
Out[2]=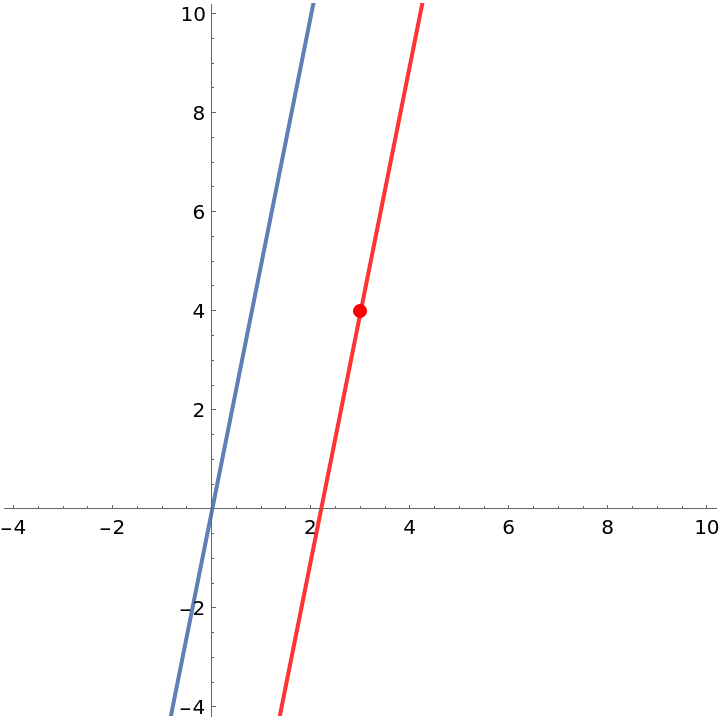

Compute the slope of this line:

In[3]:=
ResourceFunction["ParallelLineThrough"][5 x, {x, 3}, {y, 4}, "Slope"]
Out[3]=

Compute the horizontal intercept of this line:

In[4]:=
ResourceFunction["ParallelLineThrough"][ 5 x, {x, 3}, {y, 4}, "HorizontalIntercept"]
Out[4]=

Get the standard form equation of this line:

In[5]:=
ResourceFunction["ParallelLineThrough"][ 5 x, {x, 3}, {y, 4}, "StandardFormEquation"]
Out[5]=

Get an Association of properties of a line parallel to y=-x/2+4 that passes through the point (x,y)=(3/5,6/7):

In[6]:=
ResourceFunction["ParallelLineThrough"][-x/2 + 4, {x, 3/5}, {y, 6/7}]
Out[6]=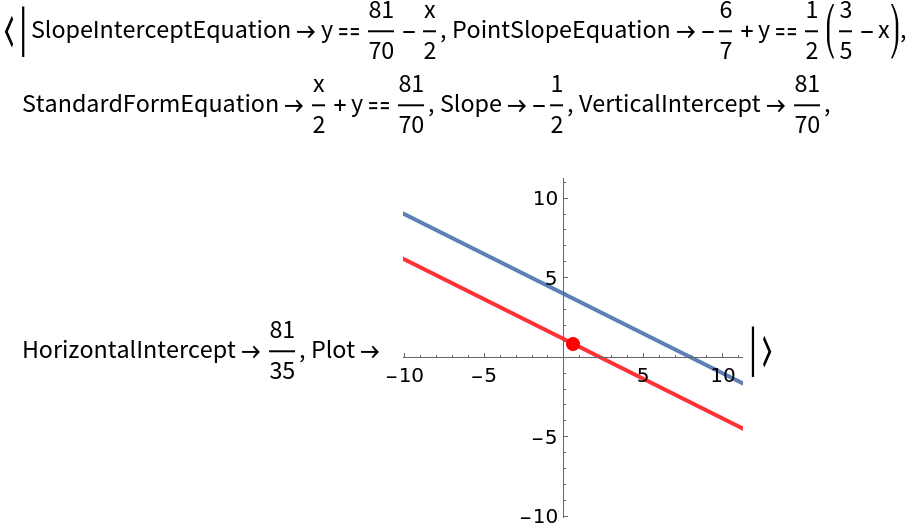

Get just the slope-intercept equation of this line:

In[7]:=
ResourceFunction[ "ParallelLineThrough"][-x/2 + 4, {x, 3/5}, {y, 6/7}, "SlopeInterceptEquation"]
Out[7]=

Possible Issues (1) 

The first argument to ParallelLineThrough must be a linear function of x:

In[8]:=
ResourceFunction["ParallelLineThrough"][x^2, {x, 1}, {y, 2}]
Out[8]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 2.0.0 – 23 March 2023
  • 1.0.0 – 05 April 2022

Related Resources

Author Notes

To view the full source code for SecantLine, evaluate the following:

In[1]:=
SystemOpen[ FileNameJoin[{DirectoryName[FindFile["ResourceFunctionHelpers`"]], "Lines.wl"}]]

License Information