Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Weber parabolic cylinder function U
ResourceFunction["ParabolicCylinderU"][a,z] gives the Weber parabolic cylinder function U(a,z). |
Evaluate numerically:
| In[1]:= |
|
| Out[1]= |
|
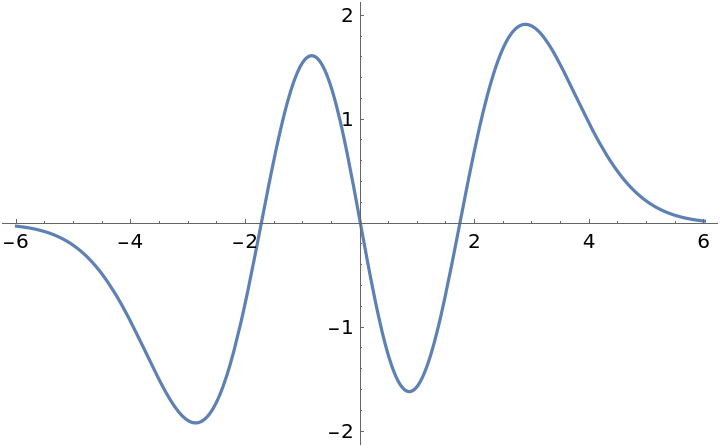
Plot ![]() :
:
| In[2]:= |
|
| Out[2]= |
|
Series expansion at the origin:
| In[3]:= |
|
| Out[3]= |
|
Evaluate for complex arguments and parameters:
| In[4]:= |
|
| Out[4]= |
|
Evaluate to high precision:
| In[5]:= |
|
| Out[5]= |
|
The precision of the output tracks the precision of the input:
| In[6]:= |
|
| Out[6]= |
|
Simple exact input gives exact results:
| In[7]:= |
|
| Out[7]= |
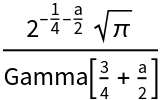
|
ParabolicCylinderU threads elementwise over lists:
| In[8]:= |
|
| Out[8]= |
|
ParabolicCylinderU satisfies the Weber differential equation:
| In[9]:= |
|
| Out[9]= |
|
A recurrence relation satisfied by ParabolicCylinderU:
| In[10]:= |
![x ResourceFunction["ParabolicCylinderU"][a, x] - ResourceFunction["ParabolicCylinderU"][a - 1, x] + (a + 1/2) ResourceFunction["ParabolicCylinderU"][a + 1, x] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/153/153bedf1-22b8-4b33-a181-dfa000583c4f/5d9ca1e84300c180.png)
|
| Out[10]= |
|
Verify an expression for the derivative:
| In[11]:= |
![D[ResourceFunction["ParabolicCylinderU"][a, x], x] == x/2 ResourceFunction["ParabolicCylinderU"][a, x] - ResourceFunction["ParabolicCylinderU"][a - 1, x] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/153/153bedf1-22b8-4b33-a181-dfa000583c4f/30f4d8bdbfd2e98d.png)
|
| Out[11]= |
|
Express ParabolicCylinderU in terms of ParabolicCylinderV:
| In[12]:= |
![ResourceFunction["ParabolicCylinderU"][a, x] == \[Pi]/(
Cos[a \[Pi]]^2 Gamma[
a + 1/2]) (ResourceFunction["ParabolicCylinderV"][a, -x] - Sin[a \[Pi]] ResourceFunction["ParabolicCylinderV"][a, x]) // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/153/153bedf1-22b8-4b33-a181-dfa000583c4f/27310f36eb9877c8.png)
|
| Out[12]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License