Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Multidimensional scaling algorithm for embedding pairwise distances into a Cartesian space
ResourceFunction["PairwiseMultidimensionalScaling"][dm] return a list of 2-dimensional coordinates representing embedding of a distance matrix dm. | |
ResourceFunction["PairwiseMultidimensionalScaling"][dm,dim] embed into a given integer dimension dim. |
Compute 2-dimensional embedding from a distance matrix of three points:
| In[1]:= | ![ResourceFunction["PairwiseMultidimensionalScaling"][( {
{0., 1., 2.},
{1., 0., 3.},
{2., 4., 0.}
} )]](https://www.wolframcloud.com/obj/resourcesystem/images/41e/41e5aac3-5c0b-4f60-a6df-7c9f78c16aae/17559ffc19008d54.png) |
| Out[1]= |
Compute 3-dimensional embedding from a distance matrix of four points:
| In[2]:= | ![ResourceFunction["PairwiseMultidimensionalScaling"][( {
{0., 1., 2., 3.},
{4., 0., 5., 6.},
{7., 8., 0., 9.},
{-1., -2., -3., 0.}
} ), 3]](https://www.wolframcloud.com/obj/resourcesystem/images/41e/41e5aac3-5c0b-4f60-a6df-7c9f78c16aae/6251d5e1d091821d.png) |
| Out[2]= |
Coordinatize an edge-weighted graph:
| In[3]:= | ![With[{g = Graph[{1 \[UndirectedEdge] 2, 2 \[UndirectedEdge] 3, 3 \[UndirectedEdge] 1}, EdgeWeight -> {1 \[UndirectedEdge] 2 -> 1.9}]},
Graph[g, VertexCoordinates -> ResourceFunction["PairwiseMultidimensionalScaling"][
GraphDistanceMatrix[g]]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/41e/41e5aac3-5c0b-4f60-a6df-7c9f78c16aae/4f9432153859a529.png) |
| Out[3]= | 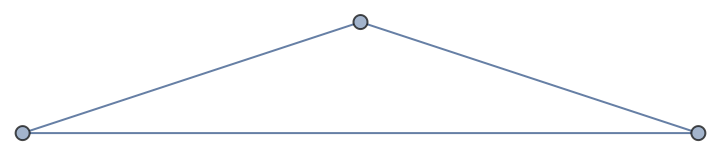 |
Coordinatize a graph given pairwise distances between vertices:
| In[4]:= |
| Out[5]= | 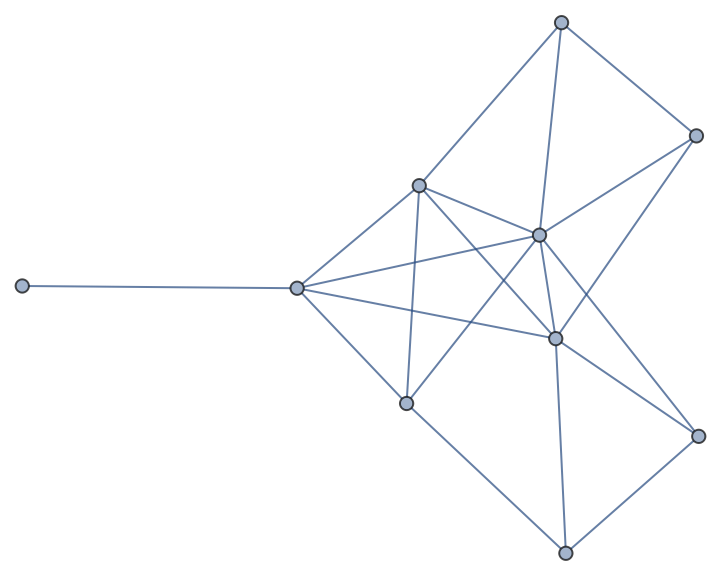 |
Providing distances of its GraphEmbedding the original graph can be closely reconstructed (up-to translational/rotational/reflectional symmetry):
| In[6]:= | ![Graph[g, VertexCoordinates -> ResourceFunction["PairwiseMultidimensionalScaling"][
DistanceMatrix[GraphEmbedding[g]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/41e/41e5aac3-5c0b-4f60-a6df-7c9f78c16aae/194aa2ae21656224.png) |
| Out[6]= | 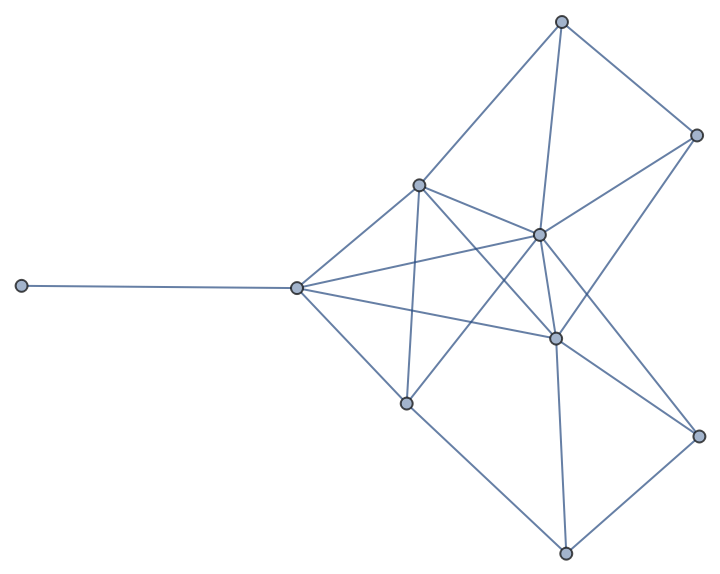 |
Coordinatize a causal graph:
| In[7]:= |
| Out[8]= |  |
| In[9]:= | ![Graph[cg, VertexCoordinates -> ResourceFunction["PairwiseMultidimensionalScaling"][
DistanceMatrix[GraphEmbedding[cg]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/41e/41e5aac3-5c0b-4f60-a6df-7c9f78c16aae/4787f67a19602db0.png) |
| Out[9]= | 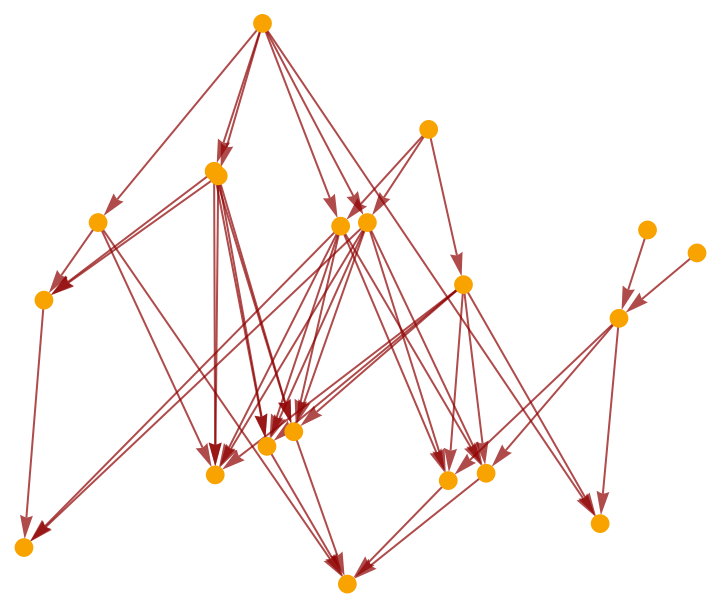 |
PairwiseMultidimensionalScaling embedding is homomorphic to the one computed using ResourceFunction[“MultidimensionalScaling”] for a DistanceMatrix with DistanceFunction → EuclideanDistance, and also similar to DimensionReduce with various methods:
| In[10]:= | ![With[{vectors = ExampleData[{"MachineLearning", "FisherIris"}, "Data"][[All, 1]]}, GraphicsRow[ListPlot /@ {
ResourceFunction["PairwiseMultidimensionalScaling"][
DistanceMatrix[vectors, DistanceFunction -> EuclideanDistance]],
ResourceFunction["MultidimensionalScaling"][vectors],
Map[{{0, 1}, {-1, 0}} . # &, DimensionReduce[vectors, Method -> "MultidimensionalScaling"]],
Map[{{-1, 0}, {0, 1}} . # &, DimensionReduce[Standardize[vectors, Mean, 1 &], Method -> "LatentSemanticAnalysis"]],
Map[{{-1, 0}, {0, 1}} . # &, DimensionReduce[vectors, Method -> "PrincipalComponentsAnalysis"]]
}, Frame -> All, ImageSize -> Full]
]](https://www.wolframcloud.com/obj/resourcesystem/images/41e/41e5aac3-5c0b-4f60-a6df-7c9f78c16aae/4c408b5cbb3f4d0e.png) |
| Out[10]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License