Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PaduaInterpolation

Source Notebook

Construct an interpolating polynomial approximation of a function using the Padua points

Contributed by: Jan Mangaldan

ResourceFunction["PaduaInterpolation"][expr,{x,xmin,xmax},{y,ymin,ymax}]

evaluates expr with x running from xmin to xmax and y running from ymin to ymax, and constructs a ResourceFunction["PaduaInterpolation"] object which represents an approximate bivariate function corresponding to the result.

ResourceFunction["PaduaInterpolation"][…][x,y]

evaluates the interpolating function with particular arguments x and y.

Details and Options

The Padua points are a unisolvent point set that can be used to interpolate and integrate a bivariate function over a rectangular domain. ResourceFunction["PaduaInterpolation"] evaluates expr at the Padua points, and implicitly constructs an interpolating polynomial passing through them.
ResourceFunction["PaduaInterpolation"] takes the following options:
InterpolationOrder15order of the interpolating polynomial generated
"PaduaType"1type of Padua points to use
WorkingPrecisionMachinePrecisionthe precision used in internal computations
Possible types of Padua points are 1, 2, 3 and 4.

Examples

Basic Examples (3) 

Construct the Padua interpolant corresponding to the function Sin[π x+Sin[π y]]:

In[1]:=
f = ResourceFunction["PaduaInterpolation"][ Sin[\[Pi] x + Sin[\[Pi] y]], {x, -1, 1}, {y, -1, 1}];

See the value at zero:

In[2]:=
f[0, 0]
Out[2]=

Plot the Padua interpolant along with the original function:

In[3]:=
Plot3D[{f[x, y], Sin[\[Pi] x + Sin[\[Pi] y]]}, {x, -1, 1}, {y, -1, 1}]
Out[3]=

Scope (2) 

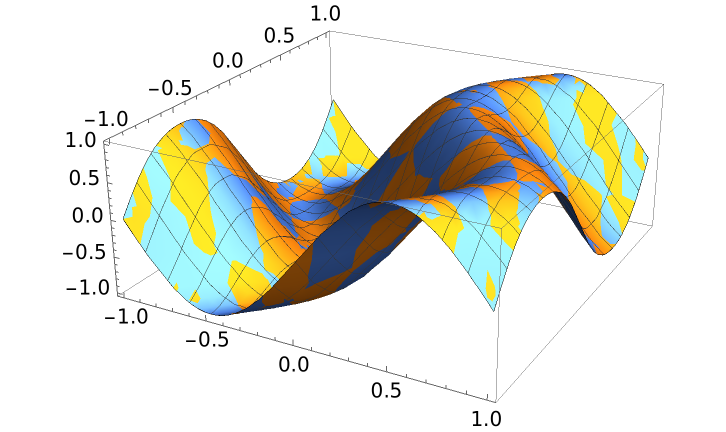See an interpolation function:

In[4]:=
interpfunc = ResourceFunction["PaduaInterpolation"][ Sin[\[Pi] x + Sin[\[Pi] y]], {x, -1, 1}, {y, -1, 1}]
Out[4]=

Get values for a few points:

In[5]:=
interpfunc @@@ {{1, 1}, {0, 1}, {-1, 0}}
Out[5]=

A test function due to Franke:

In[6]:=
franke[x_, y_] := 3/4 Exp[-(((9 x - 2)^2 + (9 y - 2)^2)/4)] + 3/4 Exp[-((9 x + 1)^2/49) - (9 y + 1)/10] + 1/2 Exp[-(((9 x - 7)^2 + (9 y - 3)^2)/4)] - 1/5 Exp[-(9 x - 4)^2 - (9 y - 7)^2]

Interpolate and plot over a rectangular domain:

In[7]:=
f = ResourceFunction["PaduaInterpolation"][ franke[x, y], {x, 0, 1}, {y, 0, 1/2}]; Plot3D[f[x, y], {x, 0, 1}, {y, 0, 1/2}, BoxRatios -> Automatic]
Out[8]=

Options (3) 

InterpolationOrder (1) 

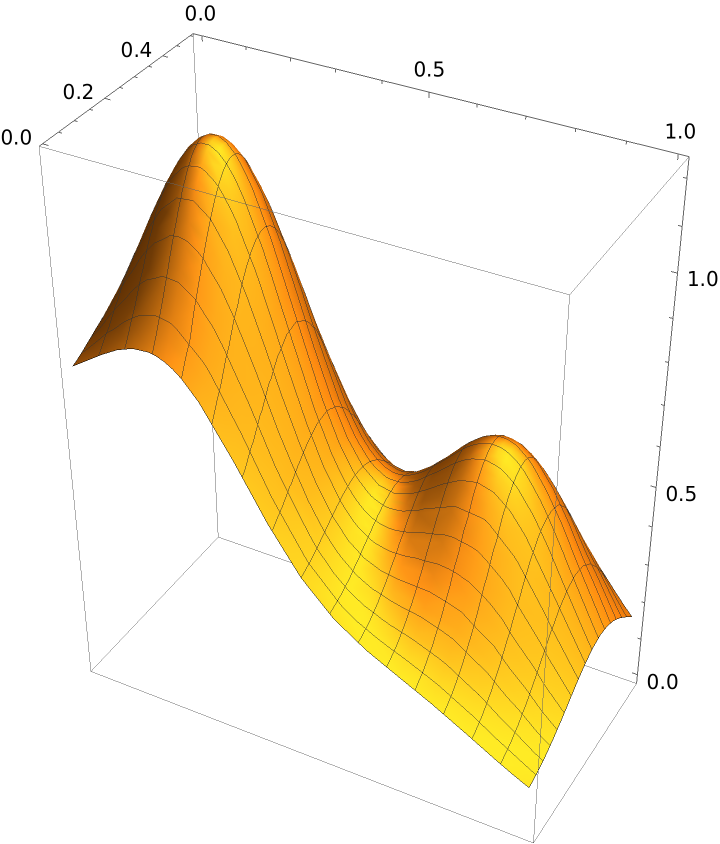Construct a Padua interpolant of the Dixon–Szegö function of degree 25:

In[9]:=
f = ResourceFunction[ "PaduaInterpolation"][(4 - 2.1 x^2 + x^4/3) x^2 + x y + 4 (y^2 - 1) y^2, {x, -2, 2}, {y, -1.25, 1.25}, InterpolationOrder -> 25]; ContourPlot[f[x, y], {x, -2, 2}, {y, -1.25, 1.25}, AspectRatio -> Automatic, Contours -> 20]
Out[9]=

PaduaType (1) 

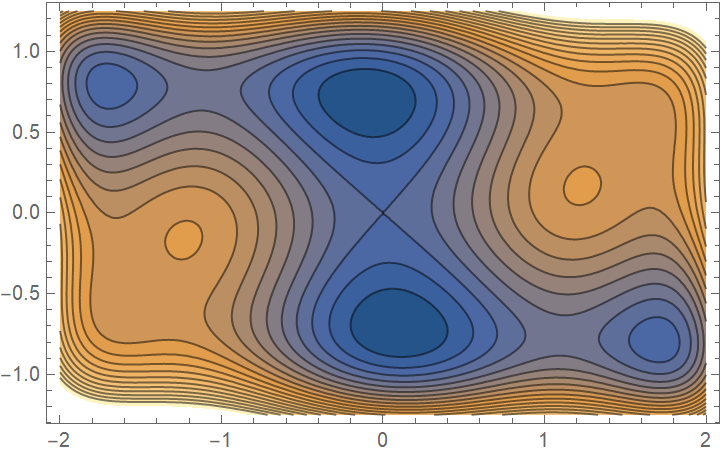Use type 3 Padua points in interpolating the Dixon–Szegö function:

In[10]:=
f = ResourceFunction[ "PaduaInterpolation"][(4 - 2.1 x^2 + x^4/3) x^2 + x y + 4 (y^2 - 1) y^2, {x, -2, 2}, {y, -1.25, 1.25}, "PaduaType" -> 3]; ContourPlot[f[x, y], {x, -2, 2}, {y, -1.25, 1.25}, AspectRatio -> Automatic, Contours -> 20]
Out[10]=

WorkingPrecision (1) 

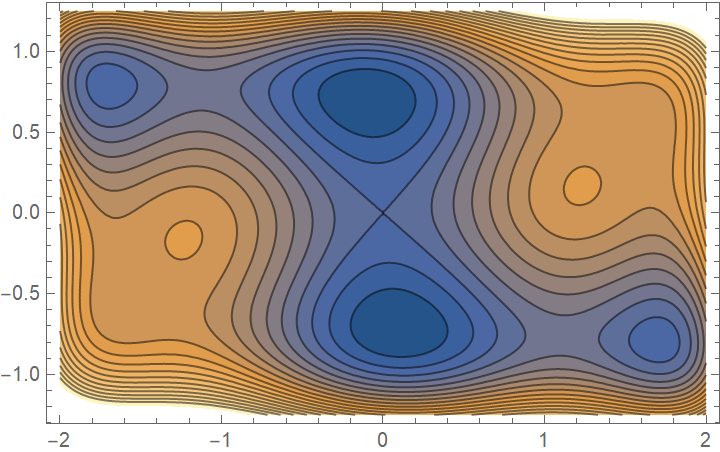Use 25-digit precision in the interpolation:

In[11]:=
f = ResourceFunction[ "PaduaInterpolation"][(4 - 21/10 x^2 + x^4/3) x^2 + x y + 4 (y^2 - 1) y^2, {x, -2, 2}, {y, -(5/4), 5/4}, WorkingPrecision -> 25]; f[1, 1]
Out[11]=

Properties and Relations (2) 

If the input function is a polynomial of degree k, PaduaInterpolation reproduces the original polynomial as long as k is less than the setting for InterpolationOrder:

In[12]:=
f = ResourceFunction["PaduaInterpolation"][ x^2 (1 + y)^3 + y^2, {x, -3, 3}, {y, -3, 3}, InterpolationOrder -> 5]; Plot3D[f[x, y] - (x^2 (1 + y)^3 + y^2), {x, -3, 3}, {y, -3, 3}]
Out[13]=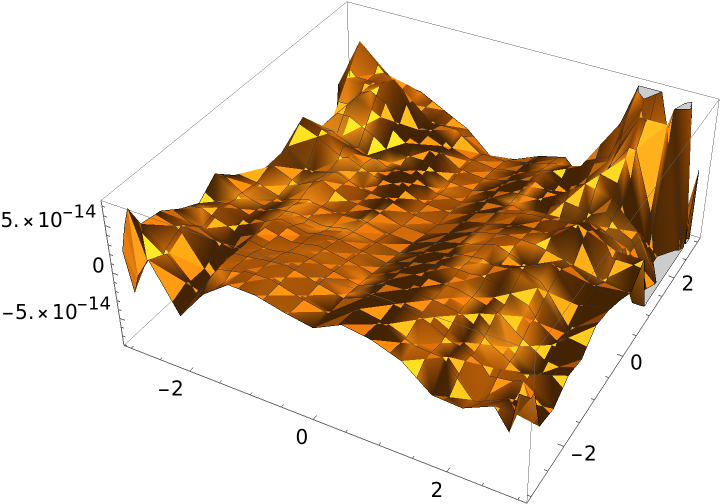

A test function due to Franke:

In[14]:=
franke[x_, y_] := 3/4 Exp[-(((9 x - 2)^2 + (9 y - 2)^2)/4)] + 3/4 Exp[-((9 x + 1)^2/49) - (9 y + 1)/10] + 1/2 Exp[-(((9 x - 7)^2 + (9 y - 3)^2)/4)] - 1/5 Exp[-(9 x - 4)^2 - (9 y - 7)^2]

Use the resource function PaduaPoints with InterpolatingPolynomial to construct a Padua interpolant:

In[15]:=
pts = ResourceFunction["PaduaPoints"][1, 19, {{0, 1}, {0, 1}}, 30]; Short[pip[x_, y_] = InterpolatingPolynomial[Transpose[{pts, franke @@@ pts}], {x, y}]]
Out[15]=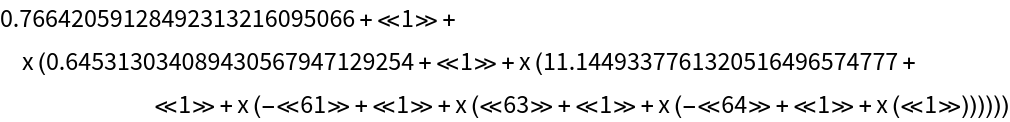

Use PaduaInterpolation to construct a Padua interpolant:

In[16]:=
pin = ResourceFunction["PaduaInterpolation"][ franke[x, y], {x, 0, 1}, {y, 0, 1}, InterpolationOrder -> 19, WorkingPrecision -> 30];

The interpolant constructed using InterpolatingPolynomial evaluates faster, but the interpolant generated by PaduaInterpolation gives a more accurate answer:

In[17]:=
AbsoluteTiming[pip[1/2, 1/2]]
Out[17]=
In[18]:=
AbsoluteTiming[pin[1/2, 1/2]]
Out[18]=

Version History

  • 1.1.0 – 22 April 2021

Source Metadata

  • Citation:
    • Bos L., Caliari M., De Marchi S., Vianello M., Xu Y., "Bivariate Lagrange interpolation at the Padua points: the generating curve approach." Journal of Approximation Theory, vol. 143, no. 1, 15–25, 2006. DOI: 10.1016/j.jat.2006.03.008
    • Caliari M., De Marchi S., Vianello M., "Bivariate polynomial interpolation on the square at new nodal sets." Applied Mathematics and Computation, vol. 165, no. 2, 261–274, 2005. DOI: 10.1016/j.amc.2004.07.001
    • Caliari M., De Marchi S., Vianello M., "Bivariate Lagrange interpolation at the Padua points: Computational aspects." Journal of Computational and Applied Mathematics, vol. 221, no. 2, 284–292, 2008. DOI: 10.1016/j.cam.2007.10.027

Related Resources

License Information