Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the osculating plane of a space curve
ResourceFunction["OsculatingPlane"][c,t] computes the osculating plane of space curve c with parameter t. |
Define a helix curve:
| In[1]:= |
| Out[1]= |
Compute the normal plane:
| In[2]:= |
| Out[2]= | 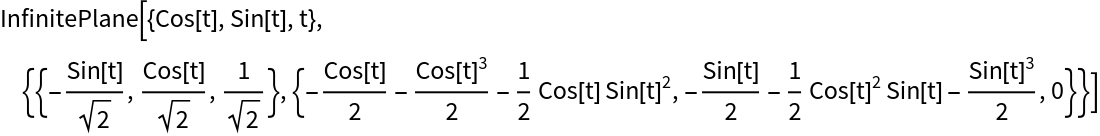 |
Plot the different planes while traversing the helix:
| In[3]:= | ![Manipulate[
With[{helix = Entity["SpaceCurve", "Helix"]["ParametricEquations"][1, 1][t]}, Show[ParametricPlot3D[helix, {t, 0, 3}], Graphics3D[{Opacity[.5], ResourceFunction["OsculatingPlane"][helix, t], ResourceFunction["RectifyingPlane"][helix, t], ResourceFunction["NormalPlane"][helix, t]} /. t -> tf], PlotRange -> {{-1, 1}, {0, 1}, {0, 3}}]], {{tf, 1}, 0, 3}]](https://www.wolframcloud.com/obj/resourcesystem/images/133/1337f653-4755-45ed-9e3a-f6f70795467f/7fa311b7f4b130dc.png) |
| Out[3]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License